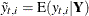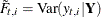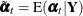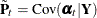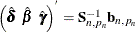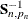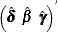The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
Smoothing Phase
After the filtering phase of KFS produces the one-step-ahead predictions of the response variables and the underlying state
vectors, the smoothing phase of KFS produces the full-sample versions of these quantities—that is, rather than using the history
up to 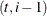 , the entire sample
, the entire sample 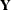 is used. The smoothing phase of KFS is a backward algorithm, which begins at
is used. The smoothing phase of KFS is a backward algorithm, which begins at 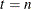 and
and 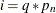 and goes back toward
and goes back toward 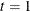 and
and 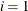 . It produces the following quantities:
. It produces the following quantities:
Table 34.8: KFS: Smoothing Phase
|
Quantity |
Description |
|---|---|
|
|
Interpolated response value |
|
|
Variance of the interpolated response value |
|
|
Full-sample estimate of the state vector |
|
|
Covariance of |
|
|
Full-sample estimates of |
|
|
Covariance of |
Note that if 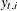 is not missing, then
is not missing, then 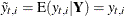 and
and 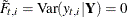 because
because 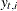 is completely known, given
is completely known, given 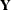 . Therefore,
. Therefore, 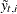 provides nontrivial information only when
provides nontrivial information only when 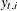 is missing—in which case
is missing—in which case 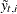 represents the best estimate of
represents the best estimate of 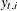 based on the available data. The full-sample estimates of components that are specified in the model equations are based
on the corresponding linear combinations of
based on the available data. The full-sample estimates of components that are specified in the model equations are based
on the corresponding linear combinations of 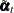 . Similarly, their standard errors are computed by using appropriate functions of
. Similarly, their standard errors are computed by using appropriate functions of 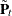 .
.
If the filtering process remains uninitialized until the end of the sample (that is, if 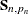 is not invertible), some linear combinations of
is not invertible), some linear combinations of 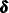 ,
, 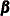 , and
, and 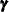 are not estimable. This, in turn, implies that some linear combinations of
are not estimable. This, in turn, implies that some linear combinations of 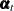 are also inestimable. These inestimable quantities are reported as missing. For more information about the estimability of
the state effects, see Selukar (2010).
are also inestimable. These inestimable quantities are reported as missing. For more information about the estimability of
the state effects, see Selukar (2010).