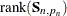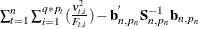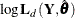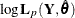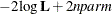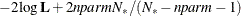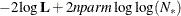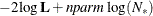The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
Likelihood Computation and Model Fitting Phase
In view of the Gaussian nature of the response vector, the likelihood of 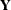 can be computed by using the prediction-error decomposition. In the diffuse case the definition of the likelihood depends
on the treatment of the diffuse quantities—
can be computed by using the prediction-error decomposition. In the diffuse case the definition of the likelihood depends
on the treatment of the diffuse quantities—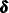 ,
, 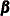 , and
, and 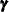 . In the SSM procedure a likelihood called the diffuse-likelihood,
. In the SSM procedure a likelihood called the diffuse-likelihood, 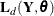 , is used for parameter estimation. In the literature the diffuse likelihood is also called the restricted-likelihood. The diffuse likelihood is computed by treating the diffuse quantities as zero-mean, Gaussian, random variables
with infinite variance (that is, they have diffuse distribution). In terms of the quantities described in Table 34.5 the diffuse likelihood is defined as follows:
, is used for parameter estimation. In the literature the diffuse likelihood is also called the restricted-likelihood. The diffuse likelihood is computed by treating the diffuse quantities as zero-mean, Gaussian, random variables
with infinite variance (that is, they have diffuse distribution). In terms of the quantities described in Table 34.5 the diffuse likelihood is defined as follows:
![\[ -2 \log \mb{L}_{d}( \mb{Y}, \pmb {\theta } ) = N_{0} \log 2 \pi + \sum _{t=1}^{n} \sum _{i=1}^{q*p_{t}} ( \log F_{t, i} + \frac{\nu _{t,i}^{2} }{ F_{t, i} } ) - \log ( | \mb{S}_{n, p_{n}}^{-1} | ) - \mb{b}_{n, p_{n}}^{'} \mb{S}_{n, p_{n}}^{-1} \mb{b}_{n, p_{n}} \]](images/etsug_ssm0225.png)
where 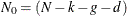 ,
, 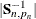 denotes the determinant of
denotes the determinant of 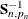 , and
, and 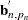 denotes the transpose of the column vector
denotes the transpose of the column vector 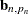 . In the preceding formula, the terms that are associated with the missing response values
. In the preceding formula, the terms that are associated with the missing response values 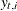 are excluded and
are excluded and 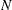 denotes the total number of nonmissing response values in the sample. If
denotes the total number of nonmissing response values in the sample. If 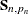 is not invertible, then a generalized inverse is used in place of
is not invertible, then a generalized inverse is used in place of 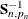 , and
, and 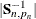 is computed based on the nonzero eigenvalues of
is computed based on the nonzero eigenvalues of 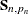 . Moreover, in this case
. Moreover, in this case 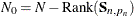 . When
. When 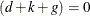 , the terms that involve
, the terms that involve 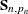 and
and 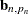 are absent.
are absent.
In addition to reporting the diffuse likelihood, the SSM procedure reports a variant of the likelihood called the profile likelihood. The profile likelihood is computed by treating the diffuse quantities—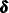 ,
, 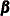 , and
, and 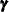 —as unknown parameters (similar to
—as unknown parameters (similar to 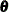 ). Interestingly, the quantities that are described in Table 34.5 play a key role in the computation of this variant of the likelihood also. It turns out that the filtering process yields
the maximum likelihood (ML) estimates of
). Interestingly, the quantities that are described in Table 34.5 play a key role in the computation of this variant of the likelihood also. It turns out that the filtering process yields
the maximum likelihood (ML) estimates of 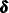 ,
, 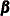 , and
, and 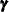 conditional on the remaining parameters of the model—
conditional on the remaining parameters of the model—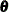 . Moreover, the likelihood that is evaluated at the ML estimates of
. Moreover, the likelihood that is evaluated at the ML estimates of 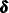 ,
, 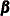 , and
, and 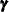 —that is, the likelihood from which these parameters are profiled out—has the following expression:
—that is, the likelihood from which these parameters are profiled out—has the following expression:
![\[ -2 \log \mb{L}_{p}( \mb{Y}, \pmb {\theta } ) = N \log 2 \pi + \sum _{t=1}^{n} \sum _{i=1}^{q*p_{t}} ( \log F_{t, i} + \frac{\nu _{t,i}^{2} }{ F_{t, i} } ) - \mb{b}_{n, p_{n}}^{'} \mb{S}_{n, p_{n}}^{-1} \mb{b}_{n, p_{n}} \]](images/etsug_ssm0235.png)
Note that, computationally, the profile likelihood differs from the diffuse likelihood in only two respects: the constant
term involves 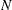 —the total number of nonmissing response values—rather than
—the total number of nonmissing response values—rather than 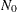 , and the log-determinant term
, and the log-determinant term 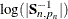 is absent. However, in terms of theoretical considerations, the diffuse likelihood and the profile likelihood differ in an
important way. It can be shown that the diffuse likelihood corresponds to the (nondiffuse) likelihood of a suitable transformation
of
is absent. However, in terms of theoretical considerations, the diffuse likelihood and the profile likelihood differ in an
important way. It can be shown that the diffuse likelihood corresponds to the (nondiffuse) likelihood of a suitable transformation
of 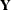 . The transformation is chosen in such a way that the distribution of the transformed data no longer depends on the initial
condition
. The transformation is chosen in such a way that the distribution of the transformed data no longer depends on the initial
condition 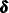 and the regression vectors
and the regression vectors 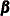 and
and 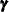 . In this sense, the diffuse likelihood is a pseudo-likelihood of the original data
. In this sense, the diffuse likelihood is a pseudo-likelihood of the original data 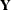 . The profile likelihood, on the other hand, does not involve any data transformation and can be considered as the likelihood
of the original data
. The profile likelihood, on the other hand, does not involve any data transformation and can be considered as the likelihood
of the original data 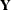 . Of course, if the state space model for
. Of course, if the state space model for 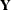 does not involve any diffuse quantities, then the two likelihoods are the same.
does not involve any diffuse quantities, then the two likelihoods are the same.
As noted earlier, the SSM procedure does not use the profile likelihood for parameter estimation. When the model specification
contains any unknown parameters 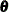 , they are estimated by maximizing the diffuse likelihood function. This is done by using a nonlinear optimization process
that involves repeated evaluations of
, they are estimated by maximizing the diffuse likelihood function. This is done by using a nonlinear optimization process
that involves repeated evaluations of 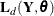 at different values of
at different values of 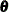 . The maximum likelihood (ML) estimate of
. The maximum likelihood (ML) estimate of 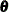 is denoted by
is denoted by 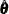 . Because the diffuse likelihood is also called the restricted likelihood,
. Because the diffuse likelihood is also called the restricted likelihood, 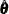 is sometimes called the restricted maximum likelihood (REML) estimate. Approximate standard errors of
is sometimes called the restricted maximum likelihood (REML) estimate. Approximate standard errors of 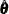 are computed by taking the square root of the diagonal elements of its (approximate) covariance matrix. This covariance is
computed as
are computed by taking the square root of the diagonal elements of its (approximate) covariance matrix. This covariance is
computed as 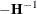 , where
, where 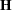 is the Hessian (the matrix of the second-order partials) of
is the Hessian (the matrix of the second-order partials) of 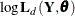 evaluated at the optimum
evaluated at the optimum 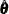 . It is known that the ML (or REML) estimate of
. It is known that the ML (or REML) estimate of 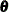 based on the diffuse likelihood as well as the profile likelihood is consistent and efficient under mild regularity assumptions
(as the number of distinct time points tend toward infinity). In addition, it is known that the estimate based on the diffuse
likelihood is better in terms of having smaller bias. For good discussions about diffuse and profile likelihoods, see Laird
(2004); Francke, Koopman, and de Vos (2010).
based on the diffuse likelihood as well as the profile likelihood is consistent and efficient under mild regularity assumptions
(as the number of distinct time points tend toward infinity). In addition, it is known that the estimate based on the diffuse
likelihood is better in terms of having smaller bias. For good discussions about diffuse and profile likelihoods, see Laird
(2004); Francke, Koopman, and de Vos (2010).
Let 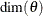 denote the dimension of the parameter vector
denote the dimension of the parameter vector 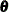 . After the parameter estimation is completed, PROC SSM prints the "Likelihood Computation Summary" table, which summarizes
the likelihood calculations at
. After the parameter estimation is completed, PROC SSM prints the "Likelihood Computation Summary" table, which summarizes
the likelihood calculations at 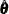 , as shown in Table 34.6.
, as shown in Table 34.6.
Table 34.6: Likelihood Computation Summary
|
Quantity |
Formula |
|---|---|
|
Nonmissing response values used |
|
|
Estimated parameters |
|
|
Initialized diffuse state elements |
|
|
Normalized residual sum of squares |
|
|
Diffuse log likelihood |
|
|
Profile log likelihood |
|
In addition, the information criteria based on the diffuse likelihood and the profile likelihood are also reported. A variety
of information criteria are reported. All these criteria are functions of twice the negative likelihood, 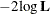 (the likelihood can be either diffuse or profile);
(the likelihood can be either diffuse or profile); 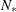 , the effective sample size; and
, the effective sample size; and 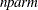 , the effective number of model parameters. For the information criteria based on the diffuse likelihood, the effective sample
size
, the effective number of model parameters. For the information criteria based on the diffuse likelihood, the effective sample
size 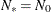 and the effective number of model parameters
and the effective number of model parameters 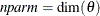 . For the information criteria based on the profile likelihood, the effective sample size
. For the information criteria based on the profile likelihood, the effective sample size 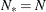 and the effective number of model parameters
and the effective number of model parameters 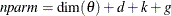 . Table 34.7 summarizes the reported information criteria in smaller-is-better form.
. Table 34.7 summarizes the reported information criteria in smaller-is-better form.
Table 34.7: Information Criteria