Usage Note 56992: Modeling continuous proportions: Fractional and 4- (or 5-) parameter logit models
 |  |  |
When modeling response data consisting of proportions (or percentages), the observed values can be continuous or represent a summarized (or aggregated) binary response. For example, an observed proportion of 0.3 might represent 3 out of 10 subjects responding positively at a particular dose of a drug. At the subject level, the response is binary (positive or negative). If your data are aggregated binary data and you have the numerator and denominator counts making up the proportions, then you can fit a logistic model in procedures such as LOGISTIC, PROBIT, GENMOD, GAM, ADAPTIVEREG and others by using the events/trials syntax in the MODEL statement. These models assume that the proportions represent a set of independent Bernoulli trials and have a binomial distribution.
However, if the values are proportions of area covered or affected by some agent, or are proportions of a mixture, then they do not represent a set of trials and might not have a binomial distribution. Modeling approaches for such data include assuming that the proportions are from normal or beta distributions as illustrated in SAS Note 57480. An approach that does not require specification of a distribution for the proportions is the fractional logistic model that uses a quasi-likelihood function for estimation. Also commonly used are 4- and 5-parameter logistic models that have a particular nonlinear form and directly estimate the ED50, the value that produces half of the predictor's effect. These models can be fit assuming a particular distribution or can also use the quasi-likelihood approach. They also allow for the response proportion to be restricted to a portion of the [0,1] range. For example, there might be a natural, non-zero response rate that occurs without exposure to the agent. This allows for a lower asymptote that is greater than zero. Similarly, it might not be possible for the maximum response proportion to reach one, requiring an upper asymptote less than one.
The data below result from an experiment on the effects of a caustic chemical. The measured response is the proportion of tissue damage that occurs at a particular site. Since damage could occur due to other causes, a non-zero natural response is expected. Also, at high enough concentrations, the chemical is likely to cause substantial, but not complete, damage. So, the maximum response is expected to be less than one.
The following statements create the data set with tissue damage proportions, Y, at various concentrations of the chemical, CONC. Note that the concentrations are approximately equally spaced on the common log scale.
data damage;
input conc y;
lconc=log10(conc);
datalines;
0.1 .08
0.25 .09
0.5 .11
1.0 .20
2 .30
4 .53
5.0 .63
8.0 .71
10.0 .73
25.0 .84
50.0 .85
100.0 .86
;
Fractional logistic model
The distribution of these proportions is not known, but if you assume that their variance behaves proportional to the variance of binomial data, then estimation can be done using a quasi-likelihood function. The quasi-likelihood behaves much like a log likelihood function when estimating a generalized linear or nonlinear model. For continuous proportion responses, a quasi-likelihood resembling the binomial log likelihood is:
1 φ log[μy(1-μ)1-y] ,
where the scale parameter, φ, is included allowing the variance to be proportional to the binomial:
Var(y) = φμ(1-μ)
The scale parameter can be estimated using the Pearson chi-square statistic.
Estimation of model parameters using this quasi-likelihood can be done using the GLIMMIX and NLMIXED procedures. The fractional logistic model is a linear logistic model and is most easily fit in PROC GLIMMIX. Since proportions are bounded between 0 and 1, it is natural to use the logit link function. To estimate the scale parameter, the random _residual_; statement is specified. The SOLUTION option displays a table of parameter estimates. The DDFM=NONE and CHISQ options are used to produce large-sample Wald tests for the parameters and fixed effects. Predicted proportions and confidence limits are saved to a data set by the OUTPUT statement.
proc glimmix data=damage;
model y = lconc / dist=binomial link=logit solution ddfm=none chisq;
random _residual_;
output out=fracout pred(ilink)=pred lcl(ilink)=lower ucl(ilink)=upper;
run;
Following are the estimated parameters of the model and Type 3 tests.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
The same model can be fit in PROC LOGISTIC by creating two new variables and two observations for each observation in the original data. The analysis is then done by weighted logistic regression as described by Liu & Xin (2014). In one observation, a new binary response variable is assigned the event level and a new weight variable is set equal to the observed proportion. In the second observation, the new binary response is assigned the nonevent level and the weight variable is set equal to one minus the observed proportion. The following DATA step makes these modifications to the tissue damage data. The Y2 variable is the new binary response variable and WT is the new weight variable. Also added is the OBS variable that contains the number of the original observation that has the same value in each pair of new observations.
data damage2;
set damage;
obs=_n_;
y2=1; wt=y; output;
y2=0; wt=1-y; output;
run;
Using these new data, the following PROC LOGISTIC step produces the same results as the PROC GLIMMIX step above using weighted logistic regression. Note that the SCALE=P and AGGREGATE=(OBS) options are specified in order to apply a scale parameter estimated by the Pearson statistic as done in the GLIMMIX analysis. The OUTPUT statement provides the same predicted values and confidence limits as from the GLIMMIX analysis. Note that only one set of the new observations is needed and is saved by the OUTPUT statement. Also note that an ROC curve and analysis can be obtained for the fractional logistic model by adding the ROCOPTIONS(WEIGHTED) option in the PROC LOGISTIC statement as well as either an ROC statement or the PLOTS=ROC option in the PROC LOGISTIC statement.
proc logistic data=damage2;
model y2(event="1") = lconc / scale=p aggregate=(obs);
weight wt;
output out=fracout(where=(y2=1)) p=pred u=upper l=lower;
run;
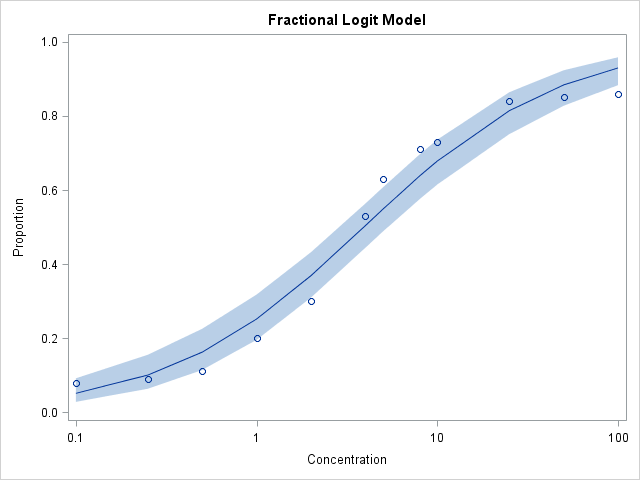
These statements plot the fitted fractional logistic model and 95% confidence bands for the mean response.
proc sgplot data=fracout noautolegend;
band upper=upper lower=lower x=conc;
scatter y=y x=conc;
series y=pred x=conc;
xaxis type=log label="Concentration";
yaxis label="Proportion" values=(0 to 1 by .2);
title "Fractional Logit Model";
run;
 |
Another example of the fractional logistic model is Quasi-likelihood Estimation for Proportions with Unknown Distribution in the Examples section of the GLIMMIX documentation (SAS Note 22930).
4- and 5-parameter logistic models
The 4-parameter logistic model is also known as the Emax model. It is a nonlinear model of the form
y = βU + βL-βU 1+(conc/β50)βS ,
where βL and βU are the lower and upper asymptotes, β50 is the ED50 (the x value producing half of the effect from lower to upper asymptote — not necessarily a 50% response unless the asymptotes are 0 and 1), and βS is the slope.
The 4-parameter model is symmetric in its tails. A model that allows for asymmetry is the 5-parameter model of the form
y = βU + βL-βU [1+(conc/β50)βS]βA ,
where βA is the asymmetry parameter.
Since these models are nonlinear in their parameters, PROC NLMIXED is used. Model estimation is done by specifying the quasi-likelihood function and using it in the GENERAL distribution option in the MODEL statement. The PARMS statement below provides initial estimates for the parameters. For these data it is sufficient to provide starting estimates for the upper and lower asymptotes. The other parameters are started at 1 by default. For some data and models, you might need to specify good starting values for all model parameters. The 4-parameter model for the mean, MU, is specified in the next line. The quasi-likelihood function, QL, is defined in the next two lines and specified in the MODEL statement. The PREDICT statement produces predicted mean values, ^ μi , for the analyzed data. The ODS OUTPUT statement saves the parameter estimates of the model in a data set.
proc nlmixed data=damage;
parms bu=.9 bl=.05;
mu = bu + (bl-bu)/(1+(conc/b50)**bs);
l = mu**y * (1-mu)**(1-y);
ql = log(l);
model y ~ general(ql);
predict mu out=out1;
ods output parameterestimates=pe;
run;
Following are estimated parameters of the initial 4-parameter logistic model.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
However, the above analysis does not estimate a scale parameter. The following statements estimate φ by using the predicted values from the initial model and the observed values to compute the Pearson chi-square statistic divided by its degrees of freedom. The degrees of freedom are n-p where p is the number of model parameters. The first SQL step below saves the number of model parameters in macro variable NPARM. The second SQL step computes the Pearson statistic:
φ = 1 n-p Σi (yi - ^ μi )2 ^ μi (1 - ^ μi )
The estimated value of φ is displayed and saved in macro variable PHI.
proc sql noprint;
select count(Parameter) into :nparm from pe;
quit;
title "Scale parameter";
title2 "Pearson Chi-square / DF";
proc sql;
select sum(phi_i) format=best12. as Scale into :phi from
(select (y-pred)**2/(pred*(1-pred)*(count(y)-&nparm)) as phi_i from out1);
quit;
title;
|
To use the estimated scale parameter, the model is refit and 1/φ is included as a multiplier in the quasi-likelihood function. Predicted mean values and 95% confidence limits are again saved using the PREDICT statement.
proc nlmixed data=damage;
parms bu=.9 bl=.05;
mu = bu + (bl-bu)/(1+(conc/b50)**bs);
l = mu**y * (1-mu)**(1-y);
ql = (1/&phi)*log(l);
model y ~ general(ql);
predict mu out=FPLout;
run;
Following is the table of parameter estimates and standard errors for the final 4-parameter logistic model.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
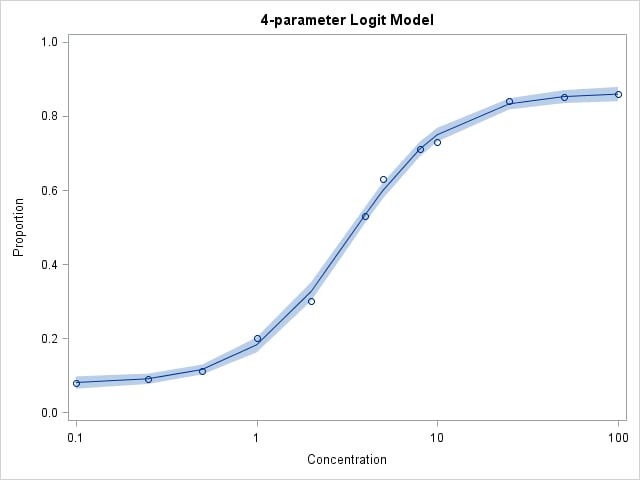
These statements plot the fitted 4-parameter logit model and 95% confidence bands for the mean response.
proc sgplot data=fplout noautolegend;
band upper=upper lower=lower x=conc;
scatter y=y x=conc;
series y=pred x=conc;
xaxis type=log label="Concentration";
yaxis label="Proportion" values=(0 to 1 by .2);
title "4-parameter Logit Model";
run;
 |
Comparison of models
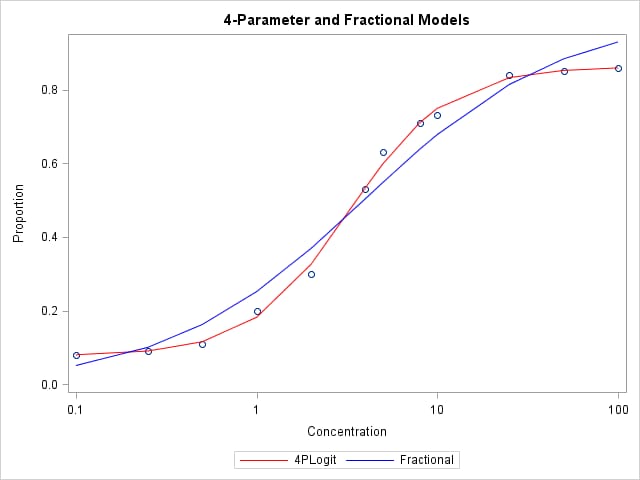
The following statements plot the fractional and 4-parameter models fit in the GLIMMIX and NLMIXED steps above.
data twomodels;
set fplout (in=fpl) fracout (in=frac);
length Model $10;
if fpl then Model="4PLogit";
else if frac then Model="Fractional";
run;
proc sgplot data=twomodels;
scatter y=y x=conc;
series y=pred x=conc / group=Model;
xaxis type=log label="Concentration";
yaxis label="Proportion";
title "4-Parameter and Fractional Models";
run;
Notice that the 4-parameter model fits much better in the tails due to its ability to use asymptotes less than 1 and greater than 0.
 |
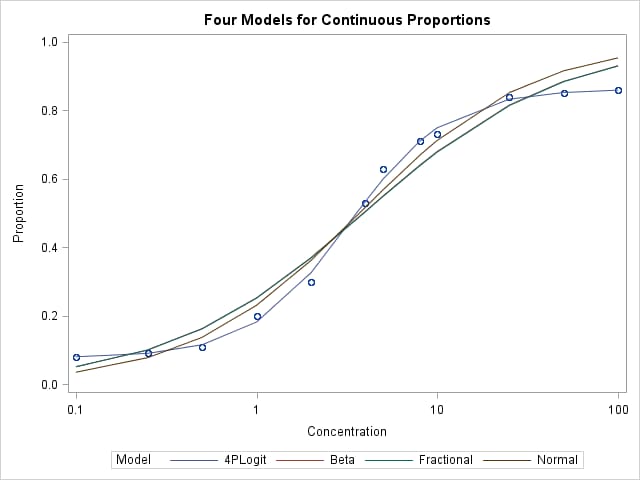
Using the predicted values saved from fitting the normal, OLS model and beta model discussed in SAS Note 57480, the following statements can be used to produce a plot showing the fits of all four models. Note that the beta and fractional logistic models are nearly identical in their fit to these data.
data fourmodels;
set fplout (in=fpl) gmxout (in=beta rename=(gpredy=pred))
fracout (in=frac) nlinout (in=norm rename=(npredy=pred));
length Model $10;
if norm then Model="Normal";
else if fpl then Model="4PLogit";
else if beta then Model="Beta";
else if frac then Model="Fractional";
run;
proc sgplot data=fourmodels;
scatter y=y x=conc;
series y=pred x=conc / group=Model;
xaxis type=log label="Concentration";
yaxis label="Proportion";
title "Four Models for Continuous Proportions";
run;
 |
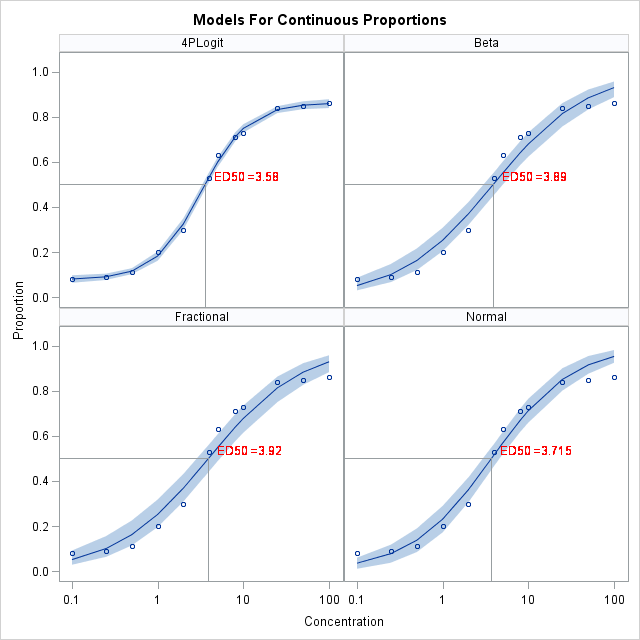
The following panel of plots shows the fits of the four models along with 95% confidence bands for the mean values. Also shown in each plot is the estimated concentration producing a 50% response (y=0.5) under each model. The normal, beta, and fractional models are all linear in the parameters, and the response function is the logit. They all have the form:
log( y 1-y) = β0 + β1log10(conc)
For y=0.5, the logit is log(1)=0. Solving for concentration, the estimate of the ED50 is 10-β0/β1. A confidence interval for the ED50 could be obtained using the methods discussed in SAS Note 56476. For the 4-parameter model, the ED50 parameter that is directly estimated by PROC NLMIXED is the estimated concentration that yields 50% of the effect from the lower to upper asymptote. For these data, that means that the ED50 estimate (3.25) yields a (0.8625+0.0769)/2 = 0.47 tissue damage proportion. Using the form of the 4-parameter model, the estimator for the concentration yielding a y=0.5 proportion is
β50( βL-βU 0.5-βU -1)1/βS
From the fitted model, the estimated concentration yielding 50% tissue damage is 3.58.
 |
__________
References
McCullagh, P. and Nelder, J.A. (1989), Generalized Linear Models 2d ed., London: Chapman & Hall/CRC.
Papke, L.E. and Wooldridge, J.M. (1996), "Econometric methods for fractional response variables with an application to 401(k) plan participation rates," J. Applied Econometrics, 11, 619-632.
Liu, W. and Xin, J. (2014), "Modeling fractional outcomes with SAS," Proceedings of the SAS Global Forum 2014 Conference, Cary, NC: SAS Institute Inc.
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | z/OS | ||
| z/OS 64-bit | ||||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> NLMIXED Analytics ==> Regression |
| Date Modified: | 2023-10-18 09:03:32 |
| Date Created: | 2015-11-02 15:47:12 |