The SURVEYSELECT Procedure

Bernoulli Sampling

Bernoulli sampling, which you request by specifying the METHOD=BERNOULLI option, is an equal probability selection method for which the total sample size is not fixed. PROC SURVEYSELECT performs an independent random selection trial for each of the N sampling units in the input data set by using the constant inclusion probability (sampling rate) that you specify. 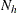You can specify a single value of the inclusion probability $\pi $ to use for all N sampling units, or you can specify separate stratum-level values of $\pi _ h$ to use for the $N_ h$ units in each stratum.

You provide the inclusion probability (or probabilities) by specifying the SAMPRATE= option. For stratified sampling (which you request by using the STRATA statement), you can specify the same sampling rate for each stratum in the SAMPRATE=value option. Or you can specify different sampling rates for different strata by using the SAMPRATE=(values) or SAMPRATE=SAS-data-set option.

In Bernoulli sampling, the sample size n (number of units selected) is not fixed; it is a random variable that has a binomial distribution with parameters N and $\pi $. The possible values of n range from 0 to N. The expected value of the sample size is $\pi N$ (or $\pi _ h N_ h$ for stratified sampling), and the variance of the sample size is $\pi (1-\pi ) N$.

For Bernoulli sampling, the selection probability is the inclusion probability that you specify in the SAMPRATE= option. PROC SURVEYSELECT computes the sampling weight as the inverse of the selection probability, which is $1 / \pi $. For Bernoulli sampling, the procedure also computes an adjusted sampling weight as the ratio of the total number of sampling units to the actual sample size, $N / n$ (or $N_ h / n_ h$ for stratified sampling). The joint selection probability for any two distinct units is $\pi ^2$. For more information, see Särndal, Swensson, and Wretman (1992).

You can specify the STATS option to include the following information in the OUT= output data set for METHOD=BERNOULLI: total number of sampling units, selection probability, expected sample size, actual sample size, sampling weight, and adjusted sampling weight.