The SURVEYIMPUTE Procedure
Replication Variance Estimation
Replication methods are useful for estimating variances that account for both the sampling variability and the imputation variability. If you specify the METHOD=FEFI option in the PROC SURVEYIMPUTE statement, then, by default, the procedure creates imputation-adjusted jackknife replicate weights unless you also specify the VARMETHOD=NONE option in the same statement. If you specify your own replicate weights by using the REPWEIGHTS statement and if you specify the METHOD=FEFI option in the PROC SURVEYIMPUTE statement, then the procedure creates new replicate weights by adjusting the replicate weights that you provide for imputation. It does not create imputation-adjusted replicate weights when you specify the METHOD=HOTDECK option in the PROC SURVEYIMPUTE statement.
The SURVEYIMPUTE procedure does not compute any variances. The replicate weights that are created can be used in any SAS/STAT survey procedure for variance computation. For an example, see the section Getting Started: SURVEYIMPUTE Procedure.
Replication methods draw multiple replicates (also called subsamples) from a full sample according to a specific resampling scheme. The most commonly used resampling schemes are the balanced repeated replication (BRR) method and the jackknife method. For each replicate, the original weights are modified for the primary sampling units (PSUs) in the replicates to create replicate weights. The parameters of interest are estimated by using the replicate weights for each replicate. These estimates are also known as replicate estimates. Then the variances of parameters of interest are estimated by estimating variability among the replicate estimates. The SURVEYIMPUTE procedure automatically creates replicate weights based on the replication method that you specify; alternatively you can use the REPWEIGHTS statement to provide your own replicate weights.
The following subsections provide details about how the replication weights are created for each variance estimation method.
Balanced Repeated Replication (BRR) Method
The balanced repeated replication (BRR) method requires that the full sample be drawn by using a stratified sample design with two primary sampling units (PSUs) per stratum. The BRR method constructs half-sample replicates by deleting one PSU per stratum according to a Hadamard matrix and doubling the original weight of the other PSU in that stratum. If you use the FEFI method, then the unadjusted BRR weights are adjusted for the imputation to create the imputation-adjusted replicate weights. The sections Unadjusted BRR Replicate Weights and Unadjusted Fay’s BRR Replicate Weights describe how the unadjusted replicate weights are created, and the section Imputation-Adjusted Replicate Weights describes how the imputation-adjusted replicate weights are created.
Unadjusted BRR Replicate Weights
Let H be the total number of strata. The total number of replicates, R, is the smallest multiple of 4 that is greater than H. However, if you prefer a larger number of replicates, you can specify the REPS=n
method-option. If an 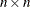 Hadamard matrix
cannot be constructed, the number of replicates is increased until a Hadamard matrix becomes available.
Hadamard matrix
cannot be constructed, the number of replicates is increased until a Hadamard matrix becomes available.
Each replicate is obtained by deleting one PSU per stratum according to a corresponding Hadamard matrix and adjusting the original weights for the remaining PSUs. The new weights are called replicate weights.
Replicates are constructed by using the first H columns of the 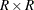 Hadamard matrix
. The rth (
Hadamard matrix
. The rth (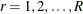 ) replicate is drawn from the full sample according to the rth row of the Hadamard matrix as follows:
) replicate is drawn from the full sample according to the rth row of the Hadamard matrix as follows:
-
If the
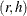 element of the Hadamard matrix is 1, then the first PSU of stratum h is included in the rth replicate and the second PSU of stratum h is excluded.
element of the Hadamard matrix is 1, then the first PSU of stratum h is included in the rth replicate and the second PSU of stratum h is excluded.
-
If the
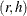 element of the Hadamard matrix is –1, then the second PSU of stratum h is included in the rth replicate and the first PSU of stratum h is excluded.
element of the Hadamard matrix is –1, then the second PSU of stratum h is included in the rth replicate and the first PSU of stratum h is excluded.
The replicate weights of the remaining PSUs in each half sample are then doubled to their original weights. For more information about the BRR method, see Wolter (2007) and Lohr (2010).
By default, PROC SURVEYIMPUTE generates an appropriate Hadamard matrix automatically to create the replicates. You can display the Hadamard matrix by specifying the VARMETHOD=BRR(PRINTH) method-option. If you provide a Hadamard matrix by specifying the VARMETHOD=BRR(HADAMARD=) method-option, then the replicates are generated according to the provided Hadamard matrix.
For more information about how the BRR variance estimators are computed for related statistics, see the section "Balanced Repeated Replication (BRR) Method" in each of the following chapters: Chapter 109: The SURVEYFREQ Procedure, Chapter 111: The SURVEYLOGISTIC Procedure, Chapter 112: The SURVEYMEANS Procedure, Chapter 113: The SURVEYPHREG Procedure, and Chapter 114: The SURVEYREG Procedure.
Unadjusted Fay’s BRR Replicate Weights
The traditional BRR method constructs half-sample replicates by deleting one PSU per stratum according to a Hadamard matrix
and doubling the original weight of the other PSU. Fay’s BRR method uses the Fay coefficient, 
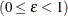 , and instead of deleting one PSU per stratum, it multiplies the original weight by the coefficient
, and instead of deleting one PSU per stratum, it multiplies the original weight by the coefficient  . The original weight of the remaining PSU in that stratum is multiplied by
. The original weight of the remaining PSU in that stratum is multiplied by 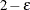 . PROC SURVEYIMPUTE uses
. PROC SURVEYIMPUTE uses 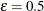 as the default value; alternatively, you can specify a value for
as the default value; alternatively, you can specify a value for  by using the FAY=
method-option. When
by using the FAY=
method-option. When 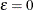 , Fay’s method becomes the traditional BRR
method. For more information, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); Judkins (1990). Because the traditional BRR method uses only half of the total sample in every replicate, some observed levels of the analysis
variables might not be available in the replicate samples. Fay’s BRR method is especially useful in this situation because
it uses all the sampled units in every replicate.
, Fay’s method becomes the traditional BRR
method. For more information, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); Judkins (1990). Because the traditional BRR method uses only half of the total sample in every replicate, some observed levels of the analysis
variables might not be available in the replicate samples. Fay’s BRR method is especially useful in this situation because
it uses all the sampled units in every replicate.
For more information about how Fay’s BRR variance estimators are computed for related statistics, see the section "Balanced Repeated Replication (BRR) Method" in each of the following chapters: Chapter 109: The SURVEYFREQ Procedure, Chapter 111: The SURVEYLOGISTIC Procedure, Chapter 112: The SURVEYMEANS Procedure, Chapter 113: The SURVEYPHREG Procedure, and Chapter 114: The SURVEYREG Procedure.
Hadamard Matrix
PROC SURVEYIMPUTE uses a Hadamard matrix to construct replicates for BRR variance estimation. You can provide a Hadamard matrix for replicate construction by using the HADAMARD= method-option for VARMETHOD=BRR . Otherwise, PROC SURVEYIMPUTE generates an appropriate Hadamard matrix. You can display the Hadamard matrix by specifying the PRINTH method-option.
A Hadamard matrix 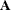 of dimension R is a square matrix that has all elements equal to 1 or –1 such that
of dimension R is a square matrix that has all elements equal to 1 or –1 such that 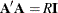 , where
, where 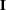 is an identity matrix of appropriate order. The dimension of a Hadamard matrix must equal 1, 2, or a multiple of 4.
is an identity matrix of appropriate order. The dimension of a Hadamard matrix must equal 1, 2, or a multiple of 4.
For example, the following matrix is a Hadamard matrix of dimension k = 8:
![\[ \begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{array} \]](images/statug_surveyimpute0055.png)
For BRR replicate construction, the dimension of the Hadamard matrix must be at least H, where H denotes the number of first-stage strata in your design. If a Hadamard matrix of a particular dimension exists, it is not necessarily unique. Therefore, if you want to use a specific Hadamard matrix, you must provide the matrix as a SAS data set in the HADAMARD= method-option. You must ensure that the matrix that you provide is actually a Hadamard matrix; PROC SURVEYIMPUTE does not check the validity of your Hadamard matrix.
For more information about how the Hadamard matrix is used to construct replicates for BRR variance estimation, see the section Unadjusted BRR Replicate Weights.
Jackknife Method
The jackknife method of variance estimation deletes one PSU at a time from the full sample to create replicates. This method
is also known as the delete-1 jackknife method because it deletes exactly one PSU in every replicate. The total number of
replicates R is the same as the total number of PSUs. In each replicate, the sampling weights of the remaining PSUs are modified by the
jackknife coefficient 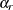 . The modified weights are called replicate weights. If you use the FEFI method, then the unadjusted replicate weights are adjusted for the imputation to create the imputation-adjusted replicate weights. The section Unadjusted Jackknife Replicate Weights describes how the unadjusted replicate weights are created, and the section Imputation-Adjusted Replicate Weights describes how the imputation-adjusted replicate weights are created.
. The modified weights are called replicate weights. If you use the FEFI method, then the unadjusted replicate weights are adjusted for the imputation to create the imputation-adjusted replicate weights. The section Unadjusted Jackknife Replicate Weights describes how the unadjusted replicate weights are created, and the section Imputation-Adjusted Replicate Weights describes how the imputation-adjusted replicate weights are created.
Unadjusted Jackknife Replicate Weights
Let PSU i in stratum 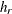 be omitted for the rth replicate. Then the jackknife coefficient,
be omitted for the rth replicate. Then the jackknife coefficient, 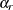 , and replicate weights,
, and replicate weights, 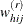 , are computed as
, are computed as
![\[ \alpha _ r = \left\{ \begin{array}{ll} \frac{ n_{h_ r} -1 }{n_{h_ r}} & \text {for a stratified design} \\[0.1in] \frac{R-1}{R} & \text {for designs without stratification} \end{array} \right. \]](images/statug_surveyimpute0059.png)
![\[ w_{hij}^{(r)} = \left\{ \begin{array}{ll} w_{hij} & \text {if observation unit } j \text { is not in donor stratum } h_ r \\ 0 & \text {if observation unit } j \text { is in PSU } i \text { of donor stratum } h_ r \\ w_{hij} / \alpha _ r & \text {if observation unit } j \text { is not in PSU } i \text { but is in donor stratum } h_ r \end{array} \right. \]](images/statug_surveyimpute0060.png)
If you use the hot-deck imputation method, then you can use the OUTPUT statement in PROC SURVEYIMPUTE to store the unadjusted replicate weights. The unadjusted replicate weights are not saved for the FEFI method. You should use the imputation-adjusted replicate weights for variance estimation from a fractionally imputed data set. Use the OUTJKCOEFS= option in the OUTPUT statement to store the jackknife coefficients in a SAS data set.
For more information about how the jackknife variance estimators are computed for related statistics, see the section "Jackknife Method" in each of the following chapters: Chapter 109: The SURVEYFREQ Procedure, Chapter 111: The SURVEYLOGISTIC Procedure, Chapter 112: The SURVEYMEANS Procedure, Chapter 113: The SURVEYPHREG Procedure, and Chapter 114: The SURVEYREG Procedure.
Imputation-Adjusted Replicate Weights
If you use the hot-deck imputation technique by specifying the METHOD=HOTDECK option in the PROC SURVEYIMPUTE statement, the procedure does not create imputation-adjusted replicate weights. Naive variance estimators that do not use imputation-adjusted replicate weights and assume the imputed data as the observed data might underestimate the true variance. For more information, see Haziza (2009); Särndal and Lundström (2005); Rao and Shao (1992).
If you use the FEFI method by specifying the METHOD=FEFI option in the PROC SURVEYIMPUTE statement, the procedure adjusts the replicate weights for imputation. The imputation-adjusted replicate weights should be used with other SAS/STAT survey procedures to estimate the variance of an estimator that uses the imputed data. For more information, see Fuller (2009, Section 5.2.2) and Kim and Shao (2014, Section 4.6).
Let 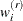 be the unadjusted replicate weight for observation unit i. To facilitate discussion, separate subscripts for strata, clusters, and imputation cells are omitted. The unadjusted replicate
weights can come from a jackknife method as described in the section Unadjusted Jackknife Replicate Weights or from a BRR method as described in the section Unadjusted BRR Replicate Weights, or they can be specified by using the REPWEIGHTS
statement. The adjustment follows the similar EM-by-weighting algorithm that is described in the section Fully Efficient Fractional Imputation but uses the replicate weights,
be the unadjusted replicate weight for observation unit i. To facilitate discussion, separate subscripts for strata, clusters, and imputation cells are omitted. The unadjusted replicate
weights can come from a jackknife method as described in the section Unadjusted Jackknife Replicate Weights or from a BRR method as described in the section Unadjusted BRR Replicate Weights, or they can be specified by using the REPWEIGHTS
statement. The adjustment follows the similar EM-by-weighting algorithm that is described in the section Fully Efficient Fractional Imputation but uses the replicate weights, 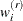 , instead of the full sample weight,
, instead of the full sample weight, 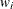 .
.
In particular, the joint probabilities for the tth M-step and the rth replicate weight are computed by
![\[ \tilde\pi _{(t)}^{(r)} (\kappa _1,\ldots ,\kappa _ P) = \left\{ \sum _ i \sum _ l w_ i^{(r)} w_{il(t-1)}^{(r)} \right\} ^{-1} \sum _ i \sum _ l w_ i^{(r)} w_{il(t-1)}^{(r)} I(Z_{i1}=\kappa _1,\ldots ,Z_{iP}=\kappa _ P) \]](images/statug_surveyimpute0062.png)
for all i, l, and 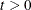 .
.
The rth replicate fractional weights for the tth E-step is computed by
![\[ w_{il(t)}^{(r)} = \left\{ \sum _{k=1}^{M_ l} \tilde\pi _{(t)}^{(r)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[k]}) \right\} ^{-1} \tilde\pi _{(t)}^{(r)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[l]}) \]](images/statug_surveyimpute0063.png)
where 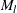 is the number of donor cells.
is the number of donor cells.
