The SURVEYIMPUTE Procedure
Hot-Deck Imputation
Imputation techniques that use observed values from the sample to impute (fill in) missing values are known as hot-deck imputation. For more information, see Fellegi and Holt (1976), Lohr (2010, Section 8.6.3), Andridge and Little (2010), Fuller (2009, Section 5.2.1), Särndal and Lundström (2005), and Bethlehem (2009, Section 8.3). The observation unit that contains the missing values is known as the recipient unit, and the observation unit that provides the value for imputation is known as the donor unit. It is common to group similar observation units in one imputation cell and then select the donor units from the same imputation cell as the recipient unit. This imputation technique is also known as hot-deck imputation within classes (Särndal, Swensson, and Wretman 1992, p. 593). If the donor unit is selected randomly for a recipient unit, then the imputation technique is called random hot-deck imputation.
PROC SURVEYIMPUTE implements cell-based random hot-deck imputation methods. You identify imputation cells by using the CELLS statement and specify a random selection method by using the SELECTION= suboption for METHOD=HOTDECK in the PROC SURVEYIMPUTE statement. If an observation unit does not contain any missing values in the analysis variables, then the observation unit is considered as a donor unit. If an observation unit contains at least one missing value in the analysis variables, then the observation unit is treated as a recipient unit. You specify the analysis variables in the VAR statement. If no donors are found for an observation unit in the imputation cell, then the missing items are not imputed for that observation unit.
To illustrate the technique, consider the data set in Figure 110.11. Assume these six units are in the same imputation cell and you want to use the hot-deck imputation to impute the missing values in units 3, 4, and 6.
Figure 110.11: Units in an Imputation Cell
The following SAS statements use units 1, 2, and 5, which contain no missing values as the donor units for all recipient units 3, 4, and 6. For every recipient unit, PROC SURVEYIMPUTE selects a donor unit at random from all available donor units and replaces the missing values in the recipient unit with the observed values from the selected donor unit.
Both Age and Pregnancy are missing for unit 6, and PROC SURVEYIMPUTE uses the same donor to impute both items. Using the same donor unit to impute
multiple items helps preserve the observed multivariate relationship.
However, it is possible to generate impossible responses. For example, if observation unit 1 is randomly selected as the donor
unit for observation unit 3, then observation unit 3 will have Gender=Male but Pregnancy=2—a biological impossibility! To deal with such situations, consider filling the deterministic values before using imputation.
For example, unit 3 is reported to be pregnant twice, and thus must be a female respondent. So you assign Gender=Female for unit 3 before using PROC SURVEYIMPUTE.
proc surveyimpute method=hotdeck(selection=srswr); var Age Gender Pregnancy; output out=JointHotDeck; run;
If you do not want to preserve the multivariate relationship among the items, then you can impute the items marginally. The
following SAS statements impute Age marginally. The recipient unit is 4, and the possible donor units are 1, 2, 3, 5, and 6.
proc surveyimpute method=hotdeck(selection=srswr); var Age; output out=MarginalHotDeck; run;
The random selection of donors preserves the expectations within the imputation cells, but the random selection process increases the variance (Fuller 2009, p. 289). The variance estimator must include both the sampling variability and the imputation variability (Särndal and Lundström 2005).
PROC SURVEYIMPUTE implements the random selection methods that are described in the following subsections.
Approximate Bayesian Bootstrap
Suppose there are m recipient units and r donor units in an imputation cell. The approximate Bayesian bootstrap technique uses the following two steps for donor selection:
-
Select a sample of size r from the r donor units by using a simple random sample with replacement. The selected set is called the donor set for this imputation cell.
-
Select m donor units from the donor set by using a simple random sample with replacement.
To account for the imputation variance, you must select multiple donor units for every recipient unit. You can use the NDONORS= option in the PROC SURVEYIMPUTE statement to select multiple donor units. The procedure repeats the preceding two steps independently to select multiple donor units for every recipient unit. If you have a stratified design, Little and Rubin (2002, p. 89) suggest defining the imputation cells that are nested within strata. By default, the procedure does not assume that the cells are nested within the strata. You must specify the STRATA variables in the CELLS statement to define the imputation cells that are nested within the strata. For more information about the approximate Bayesian bootstrap method, see Rubin and Schenker (1986), Little and Rubin (2002, p. 89), and Kim (2002).
Simple Random Samples without Replacement
Suppose there are m recipient units and r donor units in an imputation cell. PROC SURVEYIMPUTE selects a simple random sample without replacement of size m from the r donors. One requirement for this selection method is that the number of donor units must be greater than or equal to the number of the recipient units. PROC SURVEYIMPUTE uses the selection-rejection method described in Tillé (2006, p. 48). If you select multiple (d) donor units for each recipient unit (by using the NDONORS= option in the PROC SURVEYIMPUTE statement), then the procedure selects d simple random samples independently.
Simple Random Samples with Replacement
Suppose there are m recipient units and r donor units in an imputation cell. PROC SURVEYIMPUTE selects a simple random sample with replacement of size m from the r donors. If you select multiple (d) donor units for each recipient unit (by using the NDONORS= option in the PROC SURVEYIMPUTE statement), then the procedure selects d simple random samples independently.
Weighted Selection
Suppose there are m recipient units and r donor units in an imputation cell. Let 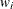 be the weight of the donor unit i. PROC SURVEYIMPUTE selects a probability proportional to donor weight,
be the weight of the donor unit i. PROC SURVEYIMPUTE selects a probability proportional to donor weight, 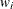 , with replacement sample of size m from the r donors. The procedure uses the probability proportional to size sampling algorithm described in Särndal, Swensson, and Wretman
(1992, p. 97). For more information about the weighted hot-deck method, see Shao and Tu (1995, p. 271), and Rao and Shao (1992).
, with replacement sample of size m from the r donors. The procedure uses the probability proportional to size sampling algorithm described in Särndal, Swensson, and Wretman
(1992, p. 97). For more information about the weighted hot-deck method, see Shao and Tu (1995, p. 271), and Rao and Shao (1992).
