The SURVEYIMPUTE Procedure

Fully Efficient Fractional Imputation

Subsections:

FEFI Algorithm
Example of FEFI

The fully efficient fractional imputation (FEFI) method uses multiple donor units for a recipient unit. The observation unit that contains the missing values is known as the recipient unit, and the observation unit that provides the value for imputation is known as the donor unit. The number of donor units for a recipient unit is equal to the number of observed levels for the missing items, given the observed levels for the nonmissing items of the recipient unit. Each donor donates a fraction of the original weight of the recipient unit such that the sum of the fractional weights from all the donors is equal to the original weight of the recipient. The fraction of the recipient weight that a donor unit contributes to the recipient unit is known as the fractional weight. The method is called fully efficient because it does not introduce additional variability that is caused by the selection of donor units (Kim and Fuller 2004). One disadvantage of the FEFI method is that it can greatly increase the size of the imputed data set. For more information, see Kalton and Kish (1984), Fuller (2009, Section 5.2.2), and Kim and Shao (2014, Section 4.6).

FEFI Algorithm

Suppose you want to impute P items jointly (by using the IMPJOINT statement in PROC SURVEYIMPUTE). Let 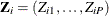$\bZ _ i=(Z_{i1},\ldots ,Z_{iP})$ be the true response for the P items for unit i. 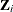$\bZ _ i$ is completely known if all P items are observed for unit i. However, the true response might not be known for some units because of item nonresponse. Let 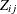$Z_{ij}$ be categorical and have J levels for item j. Denote 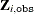$\bZ _{i,\mt {obs}}$ as the observed part and 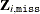$\bZ _{i,\mt {miss}}$ as the missing part of 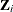$\bZ _ i$ . 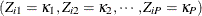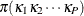Let the population proportion that falls in category $(Z_{i1}=\kappa _1,Z_{i2}=\kappa _2, \cdots , Z_{iP}=\kappa _ P)$ be $\pi (\kappa _1\kappa _2 \cdots \kappa _ P)$ . Assume that it is possible to estimate the population proportion from the observed sample. 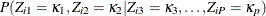That is, for example, the conditional probability, $P(Z_{i1}=\kappa _1,Z_{i2}=\kappa _2|Z_{i3}=\kappa _3,\ldots ,Z_{iP}=\kappa _ p)$ , in the observed data is the same as the conditional probability in the data where 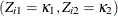$(Z_{i1}=\kappa _1,Z_{i2}=\kappa _2)$ are missing. The conditional probabilities are estimated by

$\hat P(Z_{i1}=\kappa _1,Z_{i2}=\kappa _2|Z_{i3}=\kappa _3,\ldots ,Z_{iP}=\kappa _ p) = \left\{ \sum _{\kappa _1 \kappa _2} \hat\pi (\kappa _1\kappa _2 \cdots \kappa _ P) \right\} ^{-1} \hat\pi (\kappa _1\kappa _2 \cdots \kappa _ P)$

where

$\hat\pi (\kappa _1\kappa _2 \cdots \kappa _ P) = \left\{ \sum _ i w_ i \right\} ^{-1} \sum _ i w_ i I(Z_{i1}=\kappa _1,\ldots ,Z_{iP}=\kappa _ P)$

is the estimated joint probability, 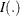$I(.)$ is an indicator function, and 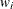$w_ i$ is the observation weight for unit i.

The FEFI method uses an EM-by-weighting algorithm similar to that of Ibrahim (1990). The detailed algorithm is described in Kim and Fuller (2013). The following steps describe the imputation technique. If you do not specify imputation cells by using the CELLS statement, PROC SURVEYIMPUTE uses the entire data set as one imputation cell. If you specify imputation cells, then all the probabilities in these steps are computed by using observations from the same imputation cell as the recipient unit. To simplify notation, subscripts are not used for imputation cells in the following description.

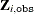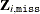For given i, let $\bZ _{i,\mt {obs}}$ and $\bZ _{i,\mt {miss}}$ be the observed part and the missing part, respectively, of unit i. Let 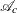$\mathcal{A}_ c$ be the index set for the complete respondents. Suppose you want to impute the missing part of 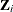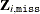$\bZ _ i$ , $\bZ _{i,\mt {miss}}$ . The index set 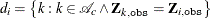$d_ i =\left\{ k: k \in \mathcal{A}_ c \wedge \bZ _{k,\mt {obs}}=\bZ _{i,\mt {obs}} \right\}$ contains the indexes for the all possible donor units for 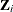$\bZ _ i$ . 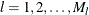Let $l=1,2,\ldots ,M_ l$ be all the observed combinations of 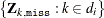$\left\{ \bZ _{k,\mt {miss}}: k \in d_ i \right\}$ . The set of all observed combinations for unit i defines the donor cells (all possible realizations) for unit i. 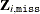Let $\bZ _{i,\mt {miss}[l]}$ be the lth imputed value of $\bZ _{i,\mt {miss}}$ . You must assume that at least one imputed value is available; otherwise the observation is not imputed.

Initialization: For each observation that has missing items, determine the number of donor cells by using the number of unique combinations of observed levels for the missing items for the responding units in the imputation cell. Compute the initial fractional weight from donor cell l to unit i, 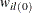$w_{il(0)}$ , by

$w_{il(0)} = \left\{ \sum _{k=1}^{M_ l} \tilde\pi _{(0)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[k]}) \right\} ^{-1} \tilde\pi _{(0)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[l]})$

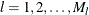where $l=1,2,\ldots ,M_ l$ is the number of donor cells, and

$\tilde\pi _{(0)} (\kappa _1,\ldots ,\kappa _ P) = \left\{ \sum _{i \in \mathcal{A}_ c} w_ i \right\} ^{-1} \sum _{i \in \mathcal{A}_ c} w_ i I(Z_{i1}=\kappa _1,\ldots ,Z_{iP}=\kappa _ P)$

The sum of the fractional weights over all the donor cells is 1 for every observation unit; that is, 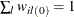$\sum _ l w_{il(0)}=1$ , for all i. The lth imputed row for unit i is created by keeping the observed items unchanged, replacing the missing items with the observed levels from the lth donor cell, and computing the fractional weight by 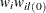$w_ i w_{il(0)}$ . Only the complete respondents are used to compute the fractional weights in this step. If unit i has no missing items, then 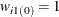$w_{i1(0)}=1$ . The initial FEFI data set contains all the observed units, the imputed rows for observation that had missing items, and the corresponding fractional weights.
M-step: The tth M-step computes the joint probabilities by using the fractional weights from the (t–1)th E-step,

$\tilde\pi _{(t)} (\kappa _1,\ldots ,\kappa _ P) = \left\{ \sum _ i \sum _ l w_ i w_{il(t-1)} \right\} ^{-1} \sum _ i \sum _ l w_ i w_{il(t-1)} I(Z_{i1}=\kappa _1,\ldots ,Z_{iP}=\kappa _ P)$

for all i, all l, and 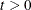$t>0$ . Note that for 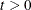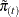$t>0$ , $\tilde\pi _{(t)}$ uses all observation units including observations that have missing items that are imputed in the initialization step.
E-step: The tth E-step computes the fractional weights by using the joint probabilities 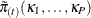$\tilde\pi _{(t)} (\kappa _1,\ldots ,\kappa _ P)$ from the tth M-step. The tth fractional weight for unit i and donor cell l is given by

$w_{il(t)} = \left\{ \sum _{k=1}^{M_ l} \tilde\pi _{(t)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[k]}) \right\} ^{-1} \tilde\pi _{(t)} (\bZ _{i,\mt {obs}},\bZ _{i,\mt {miss}[l]})$
Repetition: The EM steps are repeated for 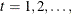$t=1,2,\ldots ,$ until the changes in fractional weights over all observation units between two successive EM steps are negligible or the maximum number of EM repetitions is reached.

The maximum absolute difference convergence criterion, 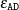$\epsilon _{\mt {AD}}$ , at step t is defined as

$\max _{i,l} \lvert {w_{il(t)}-w_{il(t-1)}} \rvert / {w_{il}} \leq \epsilon _{\mt {AD}}$

The maximum absolute relative difference convergence criterion, 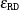$\epsilon _{\mt {RD}}$ , at step t is defined as

$\max _{i,l} \lvert {w_{il(t)}-w_{il(t-1)}} \rvert /{w_{il(t-1)}} \leq \epsilon _{\mt {RD}}$

where $w_{il(t-1)}>0$ .

The replicate weights are created by computing a replicated version of 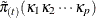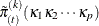$\tilde\pi _{(t)}(\kappa _1\kappa _2\cdots \kappa _ p)$ , $\tilde\pi _{(t)}^{(k)}(\kappa _1\kappa _2\cdots \kappa _ p)$ , and by repeating the EM-by-weighting algorithm as described earlier. For the kth replicate sample, 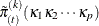$\tilde\pi _{(t)}^{(k)}(\kappa _1\kappa _2\cdots \kappa _ p)$ is computed by

$\tilde\pi _{(t)}^{(k)} (\kappa _1,\ldots ,\kappa _ P) = \left\{ \sum _ i \sum _ l w_ i^{(k)} w_{il(t-1)}^{(k)} \right\} ^{-1} \sum _ i \sum _ l w_ i^{(k)} w_{il(t-1)}^{(k)} I(Z_{i1}=\kappa _1,\ldots ,Z_{iP}=\kappa _ P)$

Example of FEFI

The small data set shown in Figure 110.8 is used to illustrate the imputation technique. The data set contains nine observation units, and each unit has two items (X and Y). The variable Unit contains the observation identification. In this example, X is missing for units 5 and 9, and Y is missing for units 2 and 9.

Figure 110.8: Sample Data with Missing Items

Unit	X	Y
1	0	0
2	0	.
3	0	1
4	0	0
5	.	1
6	1	0
7	1	1
8	1	1
9	.	.

The following SAS statements request joint imputation of X and Y by using the FEFI method. These statements also request imputation-adjusted replicate weights for the jackknife replication method. The CLASS statement specifies that both X and Y are CLASS variables. The OUTPUT statement stores the imputed values in the data set Imputed and stores the jackknife coefficients in the data set Ojkc. The FRACTIONALWEIGHTS= option in the OUTPUT statement saves the fractional weights in the Imputed data set.

proc surveyimpute data=test varmethod=jackknife;
   class x y;
   var x y;
   id Unit;
   output out=Imputed fractionalweights=FracWgt outjkcoefs=Ojkc;
run;

The initial fractional weights, FracWgt, after the initialization step are displayed in Figure 110.9.

Observation unit 1 has no missing value. Therefore, the Recipient value is 0, the FracWgt value is 1, and the values of X and Y are the same as the observed values for observation unit 1 in Figure 110.9. Because all observation units have a weight of 1, the fractional weights, FracWgt, and the imputation-adjusted weights, ImpWt, are the same for all rows.
Observation unit 2 has a missing Y. The observed level for X for unit 2 is 0. For X = 0, two levels for Y are observed: Y = 0, which has a proportion (FracWgt) of 0.67, and Y = 1, which has a proportion of 0.33. Therefore, observation unit 2 receives two donor cells (Recipient = 1 and Recipient = 2), whose initial fractional weights are 0.67 and 0.33, respectively. Because X is observed, the X values in both rows for unit 2 are the same as the observed value. However, the first recipient row for unit 2 has an imputed Y value of 0, the second recipient row for unit 2 has an imputed Y value of 1, and each has a corresponding initial fractional weight.
Observation unit 5 has a missing X. The observed level for Y for unit 5 is 1. To impute X, note that two levels of X are observed when Y = 1: X = 0 with a proportion of 0.33 and X = 1 with a proportion of 0.67. The two recipient rows for observation unit 5 contain the initial fractional weights in the FracWgt column and the imputed X values.
Observation unit 9 has missing values for both X and Y. From the observed data, X and Y can take the following values: (X = 0, Y = 0) with probability 0.33, (X = 0, Y = 1) with probability 0.17, (X = 1, Y = 0) with probability 0.17, and (X = 1, Y = 1) with probability 0.33. The four imputed rows (Recipient 1, Recipient 2, Recipient 3, and Recipient 4) for observation unit 9 represent the four observed combinations for X and Y along with their initial fractional weights.

The resulting data set contains 14 rows. There are six rows for fully observed units (Recipient = 0), two rows for unit 2, two rows for unit 5, and four rows for unit 9. The sum of initial fractional weights is 1 for all units.

Figure 110.9: Fractional Imputation after Initialization

Unit	Recipient	ImpWt	FracWgt	X	Y
1	0	1.00000	1.00000	0	0
2	1	0.66667	0.66667	0	0
2	2	0.33333	0.33333	0	1
3	0	1.00000	1.00000	0	1
4	0	1.00000	1.00000	0	0
5	1	0.33333	0.33333	0	1
5	2	0.66667	0.66667	1	1
6	0	1.00000	1.00000	1	0
7	0	1.00000	1.00000	1	1
8	0	1.00000	1.00000	1	1
9	1	0.33333	0.33333	0	0
9	2	0.16667	0.16667	0	1
9	3	0.16667	0.16667	1	0
9	4	0.33333	0.33333	1	1

The EM algorithm repeats the computation of the joint probabilities and the fractional weights until convergence. The fractional weights, FracWgt, after the EM step and the imputation-adjusted replicate weights (ImpRepWt_1, …, ImpRepWt_9) are displayed in Figure 110.10.

Figure 110.10: Fractional Imputation after the EM

Unit	Recipient	ImpWt	FracWgt	X	Y	ImpRepWt_1	ImpRepWt_2	ImpRepWt_3	ImpRepWt_4	ImpRepWt_5	ImpRepWt_6	ImpRepWt_7	ImpRepWt_8	ImpRepWt_9
1	0	1.00000	1.00000	0	0	0.00000	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500
2	1	0.58601	0.58601	0	0	0.46072	0.00000	1.12498	0.46072	0.75009	0.65906	0.62682	0.62682	0.65877
2	2	0.41399	0.41399	0	1	0.66428	0.00000	0.00002	0.66428	0.37491	0.46594	0.49818	0.49818	0.46623
3	0	1.00000	1.00000	0	1	1.12500	1.12500	0.00000	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500
4	0	1.00000	1.00000	0	0	1.12500	1.12500	1.12500	0.00000	1.12500	1.12500	1.12500	1.12500	1.12500
5	1	0.41399	0.41399	0	1	0.49821	0.37510	0.00002	0.49821	0.00000	0.46601	0.66443	0.66443	0.46623
5	2	0.58601	0.58601	1	1	0.62679	0.74990	1.12498	0.62679	0.00000	0.65899	0.46057	0.46057	0.65877
6	0	1.00000	1.00000	1	0	1.12500	1.12500	1.12500	1.12500	1.12500	0.00000	1.12500	1.12500	1.12500
7	0	1.00000	1.00000	1	1	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500	0.00000	1.12500	1.12500
8	0	1.00000	1.00000	1	1	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500	1.12500	0.00000	1.12500
9	1	0.32330	0.32330	0	0	0.22659	0.32143	0.48214	0.22659	0.42862	0.41563	0.41109	0.41109	0.00000
9	2	0.22840	0.22840	0	1	0.32669	0.21434	0.00001	0.32669	0.21424	0.29384	0.32672	0.32672	0.00000
9	3	0.12500	0.12500	1	0	0.16071	0.16071	0.16071	0.16071	0.16071	0.00000	0.16071	0.16071	0.00000
9	4	0.32330	0.32330	1	1	0.41101	0.42851	0.48214	0.41101	0.32143	0.41553	0.22648	0.22648	0.00000