The SEQTEST Procedure

Repeated Confidence Intervals

Subsections:

In a group sequential test, repeated confidence intervals for a parameter 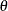$\theta $ are defined as a sequence of intervals 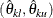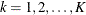$(\hat{\theta }_{kl}, \hat{\theta }_{ku})$, $k=1, 2, \ldots , K$, for which a simultaneous coverage probability is maintained (Jennison and Turnbull 2000, p. 189). That is, a 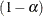$(1-\alpha )$ sequence of repeated confidence intervals has

\[ \mr{Prob} (\, \hat{\theta }_{kl} \leq \theta \leq \hat{\theta }_{ku} ) = 1 - \alpha \]

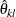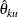These confidence limits $\hat{\theta }_{kl}$ and $\hat{\theta }_{ku}$ can be created from observed statistic and boundary values at each stage.

Two-Sided Repeated Confidence Intervals

Two sequences of repeated confidence intervals can be derived for a two-sided test. 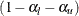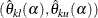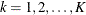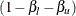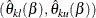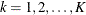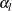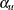One is a $(1-\alpha _{l}-\alpha _{u})$ rejection repeated confidence intervals $(\hat{\theta }_{kl}(\alpha ), \hat{\theta }_{ku}(\alpha ))$, $k=1, 2, \ldots , K$, and the other is a $(1-\beta _{l}-\beta _{u})$ acceptance repeated confidence intervals $(\hat{\theta }_{kl}(\beta ), \hat{\theta }_{ku}(\beta ))$, $k=1, 2, \ldots , K$, where $\alpha _{l}$ and $\alpha _{u}$ are the lower and upper Type I error probabilities for the test and 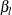$\beta _{l}$ and $\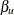beta _{u}$ are the lower and upper Type II error probabilities for the test (Jennison and Turnbull 2000, p. 196).

The rejection lower and upper repeated confidence limits at stage k are

\[ \hat{\theta }_{kl}(\alpha ) = \hat{\theta }_{k} - \frac{a_{k}}{\sqrt {I_{k}}} \, \, \, \, \, \, \, \, \, \, \, \, \hat{\theta }_{ku}(\alpha ) = \hat{\theta }_{k} - \frac{a_{\_ k}}{\sqrt {I_{k}}} \]

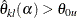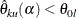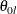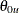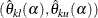The hypothesis is rejected for upper alternative if the lower limit $\hat{\theta }_{kl}(\alpha ) > \theta _{0u}$ and is rejected for lower alternative if the upper limit $\hat{\theta }_{ku}(\alpha ) < \theta _{0l}$. That is, the hypothesis is rejected if both $\theta _{0l}$ and $\theta _{0u}$ are not in a rejection repeated confidence interval $(\hat{\theta }_{kl}(\alpha ), \hat{\theta }_{ku}(\alpha ))$.

The acceptance lower and upper repeated confidence limits at stage k are

\[ \hat{\theta }_{kl}(\beta ) = \hat{\theta }_{k} + \left( \theta _{1l} - \frac{b_{\_ k}}{\sqrt {I_{k}}} \right) \, \, \, \, \, \, \, \, \, \, \, \, \hat{\theta }_{ku}(\beta ) = \hat{\theta }_{k} + \left( \theta _{1u} - \frac{b_{k}}{\sqrt {I_{k}}} \right) \]

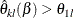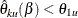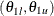The hypothesis is accepted if the lower limit $\hat{\theta }_{kl}(\beta ) > \theta _{1l}$ and the upper limit $\hat{\theta }_{ku}(\beta ) < \theta _{1u}$. That is, a repeated confidence interval is contained in the interval $(\theta _{1l}, \theta _{1u})$.

One-Sided Repeated Confidence Intervals

Like the two-sided repeated confidence intervals, two sequences of repeated confidence intervals can be derived for a one-sided test. Suppose the one-sided test has an upper alternative $\theta _{1u}$. 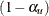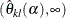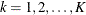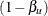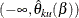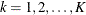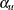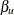Then one sequence of repeated confidence intervals is a $(1-\alpha _{u})$ rejection repeated confidence intervals $(\hat{\theta }_{kl}(\alpha ), \infty )$, $k=1, 2, \ldots , K$, and the other is a $(1-\beta _{u})$ acceptance repeated confidence intervals $(-\infty , \hat{\theta }_{ku}(\beta ))$, $k=1, 2, \ldots , K$, where $\alpha _{u}$ and $\beta _{u}$ are the upper Type I and Type II error probabilities for the test. 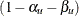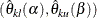Thus, a sequence of repeated confidence intervals with confidence level greater than or equal to $(1-\alpha _{u}-\beta _{u})$ is given by $(\hat{\theta }_{kl}(\alpha ), \hat{\theta }_{ku}(\beta ))$.

The rejection lower repeated confidence limit and the acceptance upper repeated confidence limit at stage k are

\[ \hat{\theta }_{kl}(\alpha ) = \hat{\theta }_{k} - \left( \frac{a_{k}}{\sqrt {I_{k}}} - \theta _{0u} \right) \, \, \, \, \, \, \, \, \, \, \, \, \hat{\theta }_{ku}(\beta ) = \hat{\theta }_{k} + \left( \theta _{1u} - \frac{b_{k}}{\sqrt {I_{k}}} \right) \]

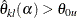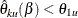The hypothesis is rejected if the lower limit $\hat{\theta }_{kl}(\alpha ) > \theta _{0u}$. and it is accepted if the upper limit $\hat{\theta }_{ku}(\beta ) < \theta _{1u}$.