The LIFETEST Procedure
Simultaneous Confidence Intervals for Kaplan-Meier Curves
The pointwise confidence interval for the survivor function 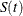 is valid for a single fixed time at which the inference is to be made. In some applications, it is of interest to find the
upper and lower confidence bands that guarantee, with a given confidence level, that the survivor function falls within the
band for all t in some interval. Hall and Wellner (1980) and Nair (1984) provide two different approaches for deriving the confidence bands.
An excellent review can be found in Klein and Moeschberger (1997). You can use the CONFBAND= option in the PROC LIFETEST statement to select the confidence bands. The EP confidence band
provides confidence bounds that are proportional to the pointwise confidence interval, while those of the HW band are not
proportional to the pointwise confidence bounds. The maximum time,
is valid for a single fixed time at which the inference is to be made. In some applications, it is of interest to find the
upper and lower confidence bands that guarantee, with a given confidence level, that the survivor function falls within the
band for all t in some interval. Hall and Wellner (1980) and Nair (1984) provide two different approaches for deriving the confidence bands.
An excellent review can be found in Klein and Moeschberger (1997). You can use the CONFBAND= option in the PROC LIFETEST statement to select the confidence bands. The EP confidence band
provides confidence bounds that are proportional to the pointwise confidence interval, while those of the HW band are not
proportional to the pointwise confidence bounds. The maximum time, 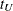 , for the bands can be specified by the BANDMAX= option; the minimum time,
, for the bands can be specified by the BANDMAX= option; the minimum time, 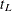 , can be specified by the BANDMIN= option. Transformations that are used to improve the pointwise confidence intervals can
be applied to improve the confidence bands. It might turn out that the upper and lower bounds of the confidence bands are
not decreasing in
, can be specified by the BANDMIN= option. Transformations that are used to improve the pointwise confidence intervals can
be applied to improve the confidence bands. It might turn out that the upper and lower bounds of the confidence bands are
not decreasing in 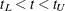 , which is contrary to the nonincreasing characteristic of survivor function. Meeker and escobar (1998) suggest making an adjustment so that the bounds do not increase: if the upper bound is increasing on the right, it is made
flat from the minimum to
, which is contrary to the nonincreasing characteristic of survivor function. Meeker and escobar (1998) suggest making an adjustment so that the bounds do not increase: if the upper bound is increasing on the right, it is made
flat from the minimum to 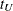 ; if the lower bound is increasing from the right, it is made flat from
; if the lower bound is increasing from the right, it is made flat from 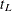 to the maximum. PROC LIFETEST does not make any adjustment for the nondecreasing behavior of the confidence bands in the
OUTSURV= data set. However, the adjustment was made in the display of the confidence bands by using ODS Graphics.
to the maximum. PROC LIFETEST does not make any adjustment for the nondecreasing behavior of the confidence bands in the
OUTSURV= data set. However, the adjustment was made in the display of the confidence bands by using ODS Graphics.
For Kaplan-Meier estimation, let 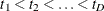 be the D distinct events times, and at time
be the D distinct events times, and at time 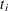 , there are
, there are 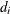 events. Let
events. Let 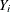 be the number of individuals who are at risk at time
be the number of individuals who are at risk at time 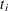 . The variance of
. The variance of 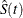 , given by the Greenwood formula, is
, given by the Greenwood formula, is ![$\hat{\sigma }^2[\hat{S}(t)] = \sigma _ S^2(t)\hat{S}^2(t)$](images/statug_lifetest0145.png) , where
, where
![\[ \sigma _ S^2(t) = \sum _{t_ i \le t} \frac{d_ i}{Y_ i(Y_ i-d_ i)} \]](images/statug_lifetest0146.png)
Let 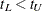 be the time range for the confidence band so that
be the time range for the confidence band so that 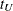 is less than or equal to the largest event time. For the Hall-Wellner band,
is less than or equal to the largest event time. For the Hall-Wellner band, 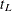 can be zero, but for the equal-precision band,
can be zero, but for the equal-precision band, 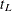 is greater than or equal to the smallest event time. Let
is greater than or equal to the smallest event time. Let
![\[ a_ L = \frac{n\sigma _ S^2(t_ L)}{1+n\sigma _ S^2(t_ L)} ~ ~ \mr{and}~ ~ a_ U = \frac{n\sigma _ S^2(t_ U)}{1+n\sigma _ S^2(t_ U)} \]](images/statug_lifetest0148.png)
Let 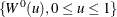 be a Brownian bridge.
be a Brownian bridge.
Hall-Wellner Band
The 100(1– )% HW band of Hall and Wellner (1980) is
)% HW band of Hall and Wellner (1980) is
![\[ \hat{S}(t) - h_\alpha (a_ L,a_ U) n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)]\hat{S}(t) \le S(t) \le \hat{S}(t) + h_\alpha (a_ L,a_ U) n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)]\hat{S}(t) \]](images/statug_lifetest0150.png)
for all 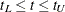 , where the critical value
, where the critical value 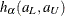 is given by
is given by
![\[ \alpha = \mr{Pr}\{ \sup _{a_ L \le u \le a_ U}|W^0(u)| > h_\alpha (a_ L,a_ U)\} \]](images/statug_lifetest0153.png)
The critical values are computed from the results in Chung (1986).
Note that the given confidence band has a formula similar to that of the (linear) pointwise confidence interval, where 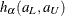 and
and ![$n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)] \hat{S}(t)$](images/statug_lifetest0155.png) in the former correspond to
in the former correspond to 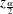 and
and 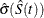 in the latter, respectively. You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for
the confidence bands by replacing
in the latter, respectively. You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for
the confidence bands by replacing 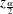 and
and 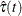 in the corresponding pointwise confidence interval formula by
in the corresponding pointwise confidence interval formula by 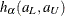 and the following
and the following 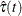 , respectively:
, respectively:
Equal-Precision Band
The 100(1– )% EP band of Nair (1984) is
)% EP band of Nair (1984) is
![\[ \hat{S}(t) - e_\alpha (a_ L,a_ U) \hat{S}(t) \sigma _ S(t) \le S(t) \le \hat{S}(t) +e_\alpha (a_ L,a_ U) \hat{S}(t) \sigma _ S(t) \]](images/statug_lifetest0162.png)
for all 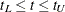 , where
, where 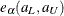 is given by
is given by
![\[ \alpha = \mr{Pr}\{ \sup _{a_ L \le u \le a_ U} \frac{|W^0(u)|}{[u(1-u)]^{\frac{1}{2}}} > e_\alpha (a_ L,a_ U)\} \]](images/statug_lifetest0165.png)
PROC LIFETEST uses the approximation of Miller and Siegmund (1982, Equation 8) to approximate the tail probability in which 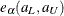 is obtained by solving x in
is obtained by solving x in
![\[ \frac{4x\phi (x)}{x} + \phi (x)\left(x-\frac{1}{x}\right)\log \left[ \frac{a_ U(1-a_ L)}{a_ L(1-a_ U)}\right] = \alpha \]](images/statug_lifetest0166.png)
where 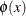 is the standard normal density function evaluated at x. Note that the confidence bounds given are proportional to the pointwise confidence intervals. As a matter of fact, this
confidence band and the (linear) pointwise confidence interval have the same formula except for the critical values (
is the standard normal density function evaluated at x. Note that the confidence bounds given are proportional to the pointwise confidence intervals. As a matter of fact, this
confidence band and the (linear) pointwise confidence interval have the same formula except for the critical values (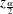 for the pointwise confidence interval and
for the pointwise confidence interval and 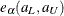 for the band). You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for the confidence
bands by replacing
for the band). You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for the confidence
bands by replacing 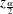 by
by 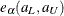 in the formula of the pointwise confidence intervals.
in the formula of the pointwise confidence intervals.

![\[ \hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{2} \sqrt {\frac{S(t)}{n[1-S(t)]}} \]](images/statug_lifetest0158.png)
![\[ \hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}} \]](images/statug_lifetest0159.png)
![\[ \hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}|\log [\hat{S}(t)]|} \]](images/statug_lifetest0160.png)
![\[ \hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}[1-\hat{S}(t)]} \]](images/statug_lifetest0161.png)