The LIFETEST Procedure

Pointwise Confidence Limits in the OUTSURV= Data Set

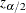Pointwise confidence limits are computed for the survivor function, and for the density function and hazard function when the life-table method is used. Let $\alpha $ be specified by the ALPHA= option. Let $z_{\alpha / 2}$ be the critical value for the standard normal distribution. That is, 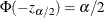$\Phi (-z_{\alpha / 2}) = \alpha / 2$, where 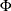$\Phi $ is the cumulative distribution function of the standard normal random variable.

Survivor Function

When the computation of confidence limits for the survivor function 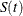$S(t)$ is based on the asymptotic normality of the survival estimator 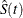$\hat{S}(t)$, the approximate confidence interval might include impossible values outside the range [0,1] at extreme values of t. This problem can be avoided by applying the asymptotic normality to a transformation of 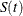$S(t)$ for which the range is unrestricted. In addition, certain transformed confidence intervals for 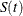$S(t)$ perform better than the usual linear confidence intervals (Borgan and Liestøl 1990). The CONFTYPE= option enables you to pick one of the following transformations: the log-log function (Kalbfleisch and Prentice 1980), the arcsine-square root function (Nair 1984), the logit function (Meeker and Escobar 1998), the log function, and the linear function.

Let g be the transformation that is being applied to the survivor function 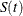$S(t)$. By the delta method, the standard error of 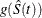$g(\hat{S}(t))$ is estimated by

\[ \tau (t) = \hat{\sigma }\left[g(\hat{S}(t))\right] = g’\left(\hat{S}(t)\right)\hat{\sigma }[\hat{S}(t)] \]

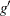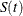where $g’$ is the first derivative of the function g. The 100(1–$\alpha $)% confidence interval for $S(t)$ is given by

\[ g^{-1}\left\{ g[\hat{S}(t)] \pm z_{\frac{\alpha }{2}} g’[\hat{S}(t)]\hat{\sigma }[\hat{S}(t)] \right\} \]

where $g^{-1}$ is the inverse function of g. That choices of the transformation g are as follows:

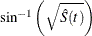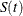  • arcsine-square root transformation: The estimated variance of $\sin ^{-1}\left(\sqrt {\hat{S}(t)}\right)$ is $ \hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{4\hat{S}(t)[1- \hat{S}(t)] }. $ The 100(1–$\alpha $)% confidence interval for $S(t)$ is given by

    \[ \sin ^2\left\{ \max \left[0,\sin ^{-1}(\sqrt {\hat{S}(t)}) - z_{\frac{\alpha }{2}} \hat{\tau }(t)\right]\right\} \le S(t) \le \sin ^2\left\{ \min \left[\frac{\pi }{2},\sin ^{-1}(\sqrt {\hat{S}(t)}) + z_{\frac{\alpha }{2}} \hat{\tau }(t)\right]\right\} \]

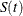  • linear transformation: This is the same as having no transformation in which g is the identity. The 100(1–$\alpha $)% confidence interval for $S(t)$ is given by

    \[ \hat{S}(t) - z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \le S(t) \le \hat{S}(t) + z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \]

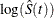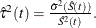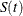  • log transformation: The estimated variance of $\log (\hat{S}(t))$ is $ \hat{\tau }^2(t) = \frac{\hat{\sigma }^2(\hat{S}(t))}{\hat{S}^2(t)}. $ The 100(1–$\alpha $)% confidence interval for $S(t)$ is given by

    \[ \hat{S}(t)\exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \le S(t) \le \hat{S}(t)\exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \]

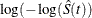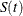  • log-log transformation: The estimated variance of $\log (-\log (\hat{S}(t))$ is $ \hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{ [\hat{S}(t)\log (\hat{S}(t))]^2 }. $ The 100(1–$\alpha $)% confidence interval for $S(t)$ is given by

    \[ \left[\hat{S}(t)\right]^{\exp \left( z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \le S(t) \le \left[\hat{S}(t)\right]^{\exp \left(-z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \]

  • logit transformation: The estimated variance of 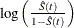$\log \left(\frac{\hat{S}(t)}{1-\hat{S}(t)}\right)$ is

    \[ \hat{\tau }^2(t) = \frac{\hat{\sigma }^2(\hat{S}(t))}{\hat{S}^2(t)[1- \hat{S}(t)]^2}. \]

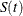    The 100(1–$\alpha $)% confidence limits for $S(t)$ are given by

    \[ \frac{\hat{S}(t)}{\hat{S}(t) + \left[1 -\hat{S}(t) \right] \exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)} \le S(t) \le \frac{\hat{S}(t)}{\hat{S}(t) + \left[1 -\hat{S}(t) \right] \exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)} \]
Density and Hazard Functions

For the life-table method, a 100(1–$\alpha $)% confidence interval for hazard function or density function at time t is computed as

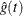\[ \hat{g}(t) \pm z_{\alpha / 2} \hat{\sigma }[\hat{g}(t)] \]

where $\hat{g}(t)$ is the estimate of either the hazard function or the density function at time t, and $\hat{\sigma }[\hat{g}(t)]$ is the corresponding standard error estimate.