The LIFETEST Procedure

Life-Table Method

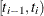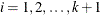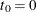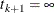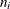The life-table estimates are computed by counting the numbers of censored and uncensored observations that fall into each of the time intervals $[t_{i-1},t_ i)$, $i=1,2,\ldots ,k+1$, where $t_0=0$ and $t_{k+1}=\infty $. Let $n_ i$ be the number of units that enter the interval 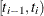$[t_{i-1},t_ i)$, and let 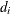$d_ i$ be the number of events that occur in the interval. Let 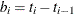$b_ i=t_ i-t_{i-1}$, and let 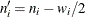$n_ i^{\prime }=n_ i - w_ i/2$, where 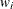$w_ i$ is the number of units censored in the interval. The effective sample size of the interval 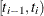$[t_{i-1},t_ i)$ is denoted by 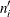$n_ i^{\prime }$. 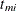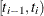Let $t_{mi}$ denote the midpoint of $[t_{i-1},t_ i)$.

The conditional probability of an event in 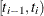$[t_{i-1},t_ i)$ is estimated by

\[ \hat{q}_ i = \frac{d_ i}{n_ i^{\prime }} \]

and its estimated standard error is

\[ \hat{\sigma } \left( \hat{q}_ i \right) = \sqrt { \frac{ \hat{q}_ i \hat{p}_ i }{ n_ i^{\prime } } } \]

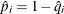where $\hat{p}_ i = 1 - \hat{q}_ i$.

The estimate of the survival function at 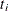$t_ i$ is

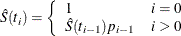
\begin{eqnarray*} \hat{S}(t_ i) = \left\{ \begin{array}{ll} 1 & i=0 \\ \hat{S}(t_{i-1})p_{i-1} & i>0 \end{array} \right. \end{eqnarray*}

and its estimated standard error is

\[ \hat{\sigma } \left( \hat{S}(t_ i) \right) = \hat{S}(t_ i) \sqrt { \sum _{j=1}^{i-1} \frac{ \hat{q}_ j }{ n_ j^{\prime } \hat{p}_ j } } \]

The density function at 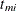$t_{mi}$ is estimated by

\[ \hat{f}(t_{mi}) = \frac{ \hat{S}(t_{i}) \hat{q}_ i }{b_ i} \]

and its estimated standard error is

\[ \hat{\sigma } \left( \hat{f}(t_{mi}) \right) = \hat{f}(t_{mi}) \sqrt { \sum _{j=1}^{i-1} \frac{ \hat{q}_ j }{ n_ j^{\prime } \hat{p}_ j } + \frac{ \hat{p}_ i }{ n_ i^{\prime } \hat{q}_ i } } \]

The estimated hazard function at 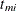$t_{mi}$ is

\[ \hat{h}(t_{mi}) = \frac{ 2 \hat{q}_ i }{ b_ i(1 + \hat{p}_ i) } \]

and its estimated standard error is

\[ \hat{\sigma } \left( \hat{h}(t_{mi}) \right) = \hat{h}(t_{mi}) \sqrt { \frac{ 1 - ( b_ i \hat{h}(t_{mi})/2 )^2 }{ n_ i^{\prime } \hat{q}_ i } } \]

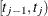Let $[t_{j-1},t_ j)$ be the interval in which 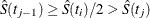$\hat{S}(t_{j-1}) \geq \hat{S}(t_ i)/2 > \hat{S}(t_ j)$. The median residual lifetime at 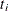$t_ i$ is estimated by

\[ \hat{M}_ i = t_{j-1} - t_ i + b_ j \frac{ \hat{S}(t_{j-1}) - \hat{S}(t_ i)/2}{ \hat{S}(t_{j-1}) - \hat{S}(t_ j) } \]

and the corresponding standard error is estimated by

\[ \hat{\sigma }(\hat{M}_ i) = \frac{ \hat{S}(t_ i) }{ 2 \hat{f}(t_{mj}) \sqrt {n_ i^{\prime }} } \]
Interval Determination

If you want to determine the intervals exactly, use the INTERVALS= option in the PROC LIFETEST statement to specify the interval endpoints. Use the WIDTH= option to specify the width of the intervals, thus indirectly determining the number of intervals. If neither the INTERVALS= option nor the WIDTH= option is specified in the life-table estimation, the number of intervals is determined by the NINTERVAL= option. The width of the time intervals is 2, 5, or 10 times an integer (possibly a negative integer) power of 10. Let 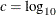$c=\log _{10}$(maximum observed time/number of intervals), and let b be the largest integer not exceeding c. Let 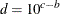$d=10^{c-b}$ and let

\[ a = 2 \times I(d \leq 2) + 5 \times I(2 < d \leq 5) + 10 \times I(d > 5) \]

with I being the indicator function. The width is then given by

\[ \mbox{width} = a \times 10^{b} \]

By default, NINTERVAL=10.