The LIFETEST Procedure
Overview: LIFETEST Procedure
A common feature of lifetime or survival data is the presence of right-censored observations due either to withdrawal of experimental units or to termination of the experiment. For such observations, you know only that the lifetime exceeded a given value; the exact lifetime remains unknown. Such data cannot be analyzed by ignoring the censored observations because, among other considerations, the longer-lived units are generally more likely to be censored. The analysis methodology must correctly use the censored observations in addition to the uncensored observations.
Texts that discuss the survival analysis methodology include Collett (1994), Cox and Oakes (1984); Kalbfleisch and Prentice (1980); Klein and Moeschberger (1997); Lawless (1982); Lee (1992). Users interested in the theory should consult Fleming and Harrington (1991); Andersen et al. (1992).
Usually, a first step in the analysis of survival data is the estimation of the distribution of the survival times. Survival times are often called failure times, and event times are uncensored survival times. The survival distribution function (SDF), also known as the survivor function, is used to describe the lifetimes of the population of interest. The SDF evaluated at t is the probability that an experimental unit from the population will have a lifetime that exceeds t—that is,
![\[ S(t) = \Pr (T > t) \]](images/statug_lifetest0001.png)
where 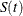 denotes the survivor function and T is the lifetime of a randomly selected experimental unit. The LIFETEST procedure can be used to compute nonparametric estimates
of the
survivor function either by the product-limit method (also called the Kaplan-Meier method) or by the life-table method (also
called the actuarial method). The life-table estimator is a grouped-data analog of the Kaplan-Meier estimator. The procedure
can also compute the Breslow estimator or the Fleming-Harrington estimator, which are asymptotic equivalent alternatives to
the Kaplan-Meier estimator.
denotes the survivor function and T is the lifetime of a randomly selected experimental unit. The LIFETEST procedure can be used to compute nonparametric estimates
of the
survivor function either by the product-limit method (also called the Kaplan-Meier method) or by the life-table method (also
called the actuarial method). The life-table estimator is a grouped-data analog of the Kaplan-Meier estimator. The procedure
can also compute the Breslow estimator or the Fleming-Harrington estimator, which are asymptotic equivalent alternatives to
the Kaplan-Meier estimator.
Some functions closely related to the SDF are the cumulative distribution function (CDF),
the probability density function (PDF),
and the hazard function.
The CDF, denoted 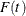 , is defined as
, is defined as 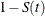 and is the probability that a lifetime does not exceed t. The PDF, denoted
and is the probability that a lifetime does not exceed t. The PDF, denoted 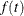 , is defined as the derivative of
, is defined as the derivative of 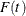 , and the hazard function, denoted
, and the hazard function, denoted 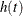 , is defined as
, is defined as 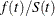 . If the life-table method is chosen, the estimates of the probability density function can also be computed. Plots of these
estimates can be produced with ODS Graphics.
. If the life-table method is chosen, the estimates of the probability density function can also be computed. Plots of these
estimates can be produced with ODS Graphics.
An important task in the analysis of survival data is the comparison of survival curves.
It is of interest to determine whether the underlying populations of k (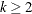 ) samples have identical survivor functions. PROC LIFETEST provides nonparametric k-sample tests based on weighted comparisons of the estimated hazard rate of the individual population under the null and alternative
hypotheses. Corresponding to various weight functions, a variety of tests can be specified, which include the log-rank test,
Wilcoxon test,
Tarone-Ware test,
Peto-Peto test,
modified Peto-Peto test,
and Fleming-Harrington
) samples have identical survivor functions. PROC LIFETEST provides nonparametric k-sample tests based on weighted comparisons of the estimated hazard rate of the individual population under the null and alternative
hypotheses. Corresponding to various weight functions, a variety of tests can be specified, which include the log-rank test,
Wilcoxon test,
Tarone-Ware test,
Peto-Peto test,
modified Peto-Peto test,
and Fleming-Harrington 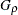 family of tests.
PROC LIFETEST also provides corresponding trend tests to detect ordered alternatives.
Stratified tests can be specified to adjust for prognostic factors that affect the events rates in the various populations.
A likelihood ratio test,
based on an underlying exponential model, is also included to compare the survival curves of the samples.
family of tests.
PROC LIFETEST also provides corresponding trend tests to detect ordered alternatives.
Stratified tests can be specified to adjust for prognostic factors that affect the events rates in the various populations.
A likelihood ratio test,
based on an underlying exponential model, is also included to compare the survival curves of the samples.
There are other prognostic variables, called covariates, that are thought to be related to the failure time. These covariates can also be used to construct statistics to test for association between the covariates and the lifetime variable. PROC LIFETEST can compute two such test statistics: censored data linear rank statistics based on the exponential scores and the Wilcoxon scores. The corresponding tests are known as the log-rank test and the Wilcoxon test, respectively. These tests are computed by pooling over any defined strata, thus adjusting for the stratum variables.
One change in SAS 9.2 and later is that the calculation of confidence limits for the quartiles of survival time is based on the transformation specified by the CONFTYPE= option. Another change is that the SURVIVAL statement in SAS 9.1 is folded into the PROC LIFETEST statement; that is, options that were in the SURVIVAL statement can now be specified in the PROC LIFETEST statement. The SURVIVAL statement is no longer needed and it is not documented.
Starting in SAS/STAT 14.1, you can use PROC LIFETEST to carry out nonparametric analysis of competing-risks data. Competing risks arise in studies in which individuals are subject to a number of potential failure events and the occurrence of one event might impede the occurrence of other events. You can use PROC LIFETEST to estimate the cumulative incidence function (CIF), which is the probability subdistribution of failure of a specific cause. If you have more than one sample of competing-risks data, you can use PROC LIFETEST to perform Gray’s test (Gray 1988) to compare the CIFs of the samples.
