The HPGENSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesExponential Family DistributionsResponse DistributionsResponse Probability Distribution FunctionsLog-Likelihood FunctionsThe LASSO Method of Model SelectionUsing Validation and Test DataComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names
Missing ValuesExponential Family DistributionsResponse DistributionsResponse Probability Distribution FunctionsLog-Likelihood FunctionsThe LASSO Method of Model SelectionUsing Validation and Test DataComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names -
Examples

- References
Example 52.3 Tweedie Model
The following HPGENSELECT statements examine the data set getStarted used in the section Getting Started: HPGENSELECT Procedure, but they request that a Tweedie model be fit by using the continuous variable Total as the response instead of the count variable Y. The following statements fit a log-linked Tweedie model to these data by using classification effects for variables C1–C5. In an insurance underwriting context, Y represents the total number of claims in each category that is defined by C1–C5, and Total represents the total cost of the claims (that is, the sum of costs for individual claims). The CODE
statement requests that a text file named "Scoring Parameters.txt" be created. This file contains a SAS program that contains
information from the model that allows scoring of a new data set based on the parameter estimates from the current model.
proc hpgenselect data=getStarted; class C1-C5; model Total = C1-C5 / Distribution=Tweedie Link=Log; code File='ScoringParameters.txt'; run;
The "Optimizations Stage Details" table in Output 52.3.1 shows the stages used in computing the maximum likelihood estimates of the parameters of the Tweedie model. Stage 1 uses quasi-likelihood and all of the data to compute starting values for stage 2, which uses all of the data and the Tweedie log likelihood to compute the final estimates.
Output 52.3.1: Optimization Stage Details
The "Parameter Estimates" table in Output 52.3.2 shows the resulting regression model parameter estimates, the estimated Tweedie dispersion parameter, and the estimated Tweedie power.
Output 52.3.2: Parameter Estimates
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Chi-Square | Pr > ChiSq |
| Intercept | 1 | 3.888904 | 0.435325 | 79.8044 | <.0001 |
| C1 0 | 1 | -0.072400 | 0.240613 | 0.0905 | 0.7635 |
| C1 1 | 1 | -1.358456 | 0.324363 | 17.5400 | <.0001 |
| C1 2 | 1 | 0.154711 | 0.237394 | 0.4247 | 0.5146 |
| C1 3 | 0 | 0 | . | . | . |
| C2 0 | 1 | 1.350591 | 0.289897 | 21.7050 | <.0001 |
| C2 1 | 1 | 1.159242 | 0.275459 | 17.7106 | <.0001 |
| C2 2 | 1 | 0.033921 | 0.303204 | 0.0125 | 0.9109 |
| C2 3 | 0 | 0 | . | . | . |
| C3 0 | 1 | -0.217763 | 0.272474 | 0.6387 | 0.4242 |
| C3 1 | 1 | -0.289425 | 0.259751 | 1.2415 | 0.2652 |
| C3 2 | 1 | -0.131961 | 0.276723 | 0.2274 | 0.6335 |
| C3 3 | 0 | 0 | . | . | . |
| C4 0 | 1 | -0.258069 | 0.288840 | 0.7983 | 0.3716 |
| C4 1 | 1 | -0.057042 | 0.287566 | 0.0393 | 0.8428 |
| C4 2 | 1 | 0.219697 | 0.272064 | 0.6521 | 0.4194 |
| C4 3 | 0 | 0 | . | . | . |
| C5 0 | 1 | -1.314657 | 0.257806 | 26.0038 | <.0001 |
| C5 1 | 1 | -0.996980 | 0.236881 | 17.7138 | <.0001 |
| C5 2 | 1 | -0.481185 | 0.235614 | 4.1708 | 0.0411 |
| C5 3 | 0 | 0 | . | . | . |
| Dispersion | 1 | 5.296966 | 0.773401 | . | . |
| Power | 1 | 1.425625 | 0.048981 | . | . |
Now suppose you want to compute predicted values for some different data. If  is a vector of explanatory variables that might not be in the original data and
is a vector of explanatory variables that might not be in the original data and 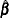 is the vector of estimated regression parameters from the model, then
is the vector of estimated regression parameters from the model, then 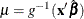 is the predicted value of the mean, where g is the log link function in this case. The following data contain new values of the regression variables
is the predicted value of the mean, where g is the log link function in this case. The following data contain new values of the regression variables C1–C5, from which you can compute predicted values based on information in the SAS program that is created by the CODE
statement. This is called scoring the new data set.
data ScoringData; input C1-C5; datalines; 3 3 1 0 2 1 1 2 2 0 3 2 2 2 0 1 1 2 3 2 1 1 2 3 3 3 1 1 0 1 0 2 1 0 0 2 1 3 1 3 3 2 3 2 0 3 0 2 0 1 ;
The following SAS DATA step creates the new data set Scores, which contains a variable P_Total that represents the predicted values of Total, along with the variables C1–C5. The resulting data are shown in Output 52.3.3.
data Scores; set ScoringData; %inc 'ScoringParameters.txt'; run; proc print data=Scores; run;
Output 52.3.3: Predicted Values for Scoring Data