The HPGENSELECT Procedure

If 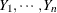are independent binary (Bernoulli) random variables that have common success probability , then their sum is a binomial random variable. In other words, a binomial random variable that has parameters n and can be generated as the sum of n Bernoulli() random experiments. The HPGENSELECT procedure uses a special syntax to express data in binomial form: the events/trials syntax.

Consider the following data, taken from Cox and Snell (1989, pp. 10–11), of the number, r, of ingots not ready for rolling, out of n tested, for a number of combinations of heating time and soaking time.

data Ingots;
   input Heat Soak r n @@;
   Obsnum= _n_;
   datalines;
7 1.0 0 10  14 1.0 0 31  27 1.0 1 56  51 1.0 3 13
7 1.7 0 17  14 1.7 0 43  27 1.7 4 44  51 1.7 0  1
7 2.2 0  7  14 2.2 2 33  27 2.2 0 21  51 2.2 0  1
7 2.8 0 12  14 2.8 0 31  27 2.8 1 22  51 4.0 0  1
7 4.0 0  9  14 4.0 0 19  27 4.0 1 16
;

If each test is carried out independently and if for a particular combination of heating and soaking time there is a constant probability that the tested ingot is not ready for rolling, then the random variable r follows a Binomial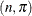 distribution, where the success probability is a function of heating and soaking time.

The following statements show the use of the events/trials syntax to model the binomial response. The events variable in this situation is r (the number of ingots not ready for rolling), and the trials variable is n (the number of ingots tested). The dependency of the probability of not being ready for rolling is modeled as a function of heating time, soaking time, and their interaction. The OUTPUT statement stores the linear predictors and the predicted probabilities in the Out data set along with the ID variable.

proc hpgenselect data=Ingots;
   model r/n = Heat Soak Heat*Soak / dist=Binomial;
   id Obsnum;
   output out=Out xbeta predicted=Pred;
run;

The "Performance Information" table in Output 52.2.1 shows that the procedure executes in single-machine mode.

The "Model Information" table shows that the data are modeled as binomially distributed with a logit link function (Output 52.2.2). This is the default link function in the HPGENSELECT procedure for binary and binomial data. The procedure uses a ridged Newton-Raphson algorithm to estimate the parameters of the model.

The second table in Output 52.2.2 shows that all 19 observations in the data set were used in the analysis and that the total number of events and trials equal 12 and 387, respectively. These are the sums of the variables r and n across all observations.

Output 52.2.3 displays the "Dimensions" table for the model. There are four columns in the design matrix of the model (the 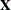matrix); they correspond to the intercept, the Heat effect, the Soak effect, and the interaction of the Heat and Soak effects. The model is nonsingular, because the rank of the crossproducts matrix equals the number of columns in 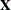. All parameters are estimable and participate in the optimization.

Output 52.2.4 displays the "Fit Statistics" table for this run. Evaluated at the converged estimates, –2 times the value of the log-likelihood function equals 27.9569. Further fit statistics are also given, all of them in "smaller is better" form. The AIC, AICC, and BIC criteria are used to compare non-nested models and to penalize the model fit for the number of observations and parameters. The –2 log-likelihood value can be used to compare nested models by way of a likelihood ratio test.

The "Parameter Estimates" table in Output 52.2.5 displays the estimates and standard errors of the model effects.

You can construct the prediction equation of the model from the "Parameter Estimates" table. For example, an observation with Heat equal to 14 and Soak equal to 1.7 has linear predictor

The probability that an ingot with these characteristics is not ready for rolling is

The OUTPUT statement computes these linear predictors and probabilities and stores them in the Out data set. This data set also contains the ID variable, which is used by the following statements to attach the covariates to these statistics. Output 52.2.6 shows the probability that an ingot with Heat equal to 14 and Soak equal to 1.7 is not ready for rolling.

data Out;
   merge Out Ingots;
   by Obsnum;
proc print data=Out;
   where Heat=14 & Soak=1.7;
run;

Binomial data are a form of grouped binary data where "successes" in the underlying Bernoulli trials are totaled. You can thus expand data for which you use the events/trials syntax and fit them with techniques for binary data.

The following DATA step expands the Ingots data set (which has 12 events in 387 trials) into a binary data set that has 387 observations.

data Ingots_binary;
   set Ingots;
   do i=1 to n;
     if i <= r then Y=1; else Y = 0;
     output;
   end;
run;

The following HPGENSELECT statements fit the model by using Heat effect, Soak effect, and their interaction to the binary data set. The event=’1’ response-variable option in the MODEL statement ensures that the HPGENSELECT procedure models the probability that the variable Y takes on the value '1'.

proc hpgenselect data=Ingots_binary;
   model Y(event='1') = Heat Soak Heat*Soak / dist=Binary;
run;

Output 52.2.7 displays the "Performance Information," "Model Information," "Number of Observations," and the "Response Profile" tables. The data are now modeled as binary (Bernoulli distributed) by using a logit link function. The "Response Profile" table shows that the binary response breaks down into 375 observations where Y equals 0 and 12 observations where Y equals 1.

Output 52.2.8 displays the parameter estimates. These results match those in Output 52.2.5.