The HPGENSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesExponential Family DistributionsResponse DistributionsResponse Probability Distribution FunctionsLog-Likelihood FunctionsThe LASSO Method of Model SelectionUsing Validation and Test DataComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names
Missing ValuesExponential Family DistributionsResponse DistributionsResponse Probability Distribution FunctionsLog-Likelihood FunctionsThe LASSO Method of Model SelectionUsing Validation and Test DataComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names -
Examples

- References
Exponential Family Distributions
Many of the probability distributions that the HPGENSELECT procedure fits are members of an exponential family of distributions, which have probability distributions that are expressed as follows for some functions b and c that determine the specific distribution:
![\[ f(y) = \exp \left\{ \frac{y\theta - b(\theta )}{\phi } + c(y,\phi ) \right\} \]](images/statug_hpgenselect0057.png)
For fixed  , this is a one-parameter exponential family of distributions. The response variable can be discrete or continuous, so
, this is a one-parameter exponential family of distributions. The response variable can be discrete or continuous, so 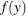 represents either a probability mass function or a probability density function. A more useful parameterization of generalized
linear models is by the mean and variance of the distribution:
represents either a probability mass function or a probability density function. A more useful parameterization of generalized
linear models is by the mean and variance of the distribution:
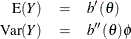
In generalized linear models, the mean 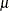 of the response distribution is related to linear regression parameters through a link function,
of the response distribution is related to linear regression parameters through a link function,
![\[ g(\mu _ i) = \mb{x}_ i^\prime \bbeta \]](images/statug_hpgenselect0060.png)
for the ith observation, where 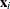 is a fixed known vector of explanatory variables and
is a fixed known vector of explanatory variables and 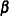 is a vector of regression parameters. The HPGENSELECT procedure parameterizes models in terms of the regression parameters
is a vector of regression parameters. The HPGENSELECT procedure parameterizes models in terms of the regression parameters
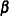 and either the dispersion parameter
and either the dispersion parameter  or a parameter that is related to
or a parameter that is related to  , depending on the model. For exponential family models, the distribution variance is
, depending on the model. For exponential family models, the distribution variance is 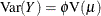 where
where 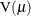 is a variance function that depends only on
is a variance function that depends only on 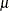 .
.
The zero-inflated models and the multinomial models are not exponential family models, but they are closely related models that are useful and are included in the HPGENSELECT procedure.