The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design - References
Example 46.3 Unbalanced ANOVA for Two-Way Design with Interaction
This example uses data from Kutner (1974, p. 98) to illustrate a two-way analysis of variance. The original data source is Afifi and Azen (1972, p. 166). These statements produce Output 46.3.1 and Output 46.3.2.
title 'Unbalanced Two-Way Analysis of Variance';
data a;
input drug disease @;
do i=1 to 6;
input y @;
output;
end;
datalines;
1 1 42 44 36 13 19 22
1 2 33 . 26 . 33 21
1 3 31 -3 . 25 25 24
2 1 28 . 23 34 42 13
2 2 . 34 33 31 . 36
2 3 3 26 28 32 4 16
3 1 . . 1 29 . 19
3 2 . 11 9 7 1 -6
3 3 21 1 . 9 3 .
4 1 24 . 9 22 -2 15
4 2 27 12 12 -5 16 15
4 3 22 7 25 5 12 .
;
proc glm; class drug disease; model y=drug disease drug*disease / ss1 ss2 ss3 ss4; run;
Output 46.3.1: Classes and Levels for Unbalanced Two-Way Design
Output 46.3.2: Analysis of Variance for Unbalanced Two-Way Design
Note the differences among the four types of sums of squares.
The Type I sum of squares for drug essentially tests for differences between the expected values of the arithmetic mean response for different drugs, unadjusted
for the effect of disease. By contrast, the Type II sum of squares for drug measures the differences between arithmetic means for each drug after adjusting for disease. The Type III sum of squares measures the differences between predicted drug means over a balanced drug disease population—that is, between the LS-means for
disease population—that is, between the LS-means for drug. Finally, the Type IV sum of squares is the same as the Type III sum of squares in this case, since there are data for every
drug-by-disease combination.
No matter which sum of squares you prefer to use, this analysis shows a significant difference among the four drugs, while
the disease effect and the drug-by-disease interaction are not significant. As the previous discussion indicates, Type III
sums of squares correspond to differences between LS-means, so you can follow up the Type III tests with a multiple-comparison
analysis of the drug LS-means.
Since the GLM procedure is interactive, you can accomplish this by submitting the following statements after the previous
ones that performed the ANOVA.
lsmeans drug / pdiff=all adjust=tukey; run;
Both the LS-means themselves and a matrix of adjusted p-values for pairwise differences between them are displayed; see Output 46.3.3 and Output 46.3.4.
Output 46.3.3: LS-Means for Unbalanced ANOVA
Output 46.3.4: Adjusted p-Values for Pairwise LS-Mean Differences
The multiple-comparison analysis shows that drugs 1 and 2 have very similar effects, and that drugs 3 and 4 are also insignificantly different from each other. Evidently, the main contribution to the significant drug effect is the difference between the 1/2 pair and the 3/4 pair.
If ODS Graphics is enabled for the previous analysis, GLM also displays three additional plots by default:
-
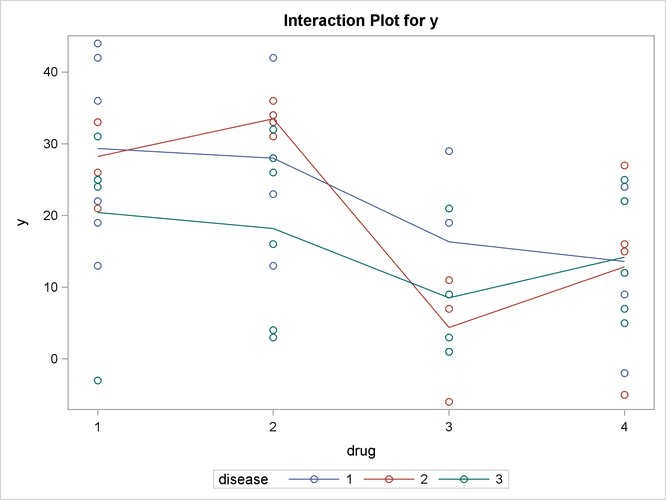
an interaction plot for the effects of disease and drug
-
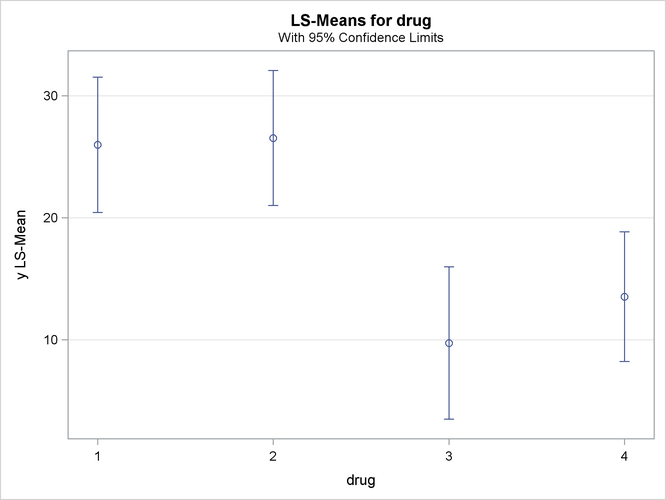
a mean plot of the drug LS-means
-
a plot of the adjusted pairwise differences and their significance levels
The following statements reproduce the previous analysis with ODS Graphics enabled. Additionally, the PLOTS= MEANPLOT(CL) option specifies that confidence limits for the LS-means should also be displayed in the mean plot. The graphical results are shown in Output 46.3.5 through Output 46.3.7.
ods graphics on; proc glm plot=meanplot(cl); class drug disease; model y=drug disease drug*disease; lsmeans drug / pdiff=all adjust=tukey; run; ods graphics off;
Output 46.3.5: Plot of Response by Drug and Disease
Output 46.3.6: Plot of Response LS-Means for Drug
Output 46.3.7: Plot of Response LS-Mean Differences for Drug
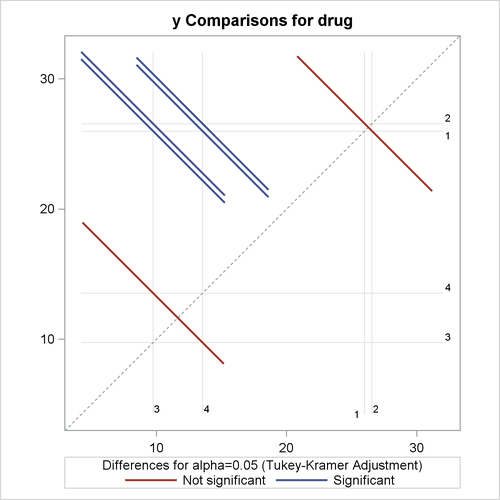
The significance of the drug differences is difficult to discern in the original data, as displayed in Output 46.3.5, but the plot of just the LS-means and their individual confidence limits in Output 46.3.6 makes it clearer. Finally, Output 46.3.7 indicates conclusively that the significance of the effect of drug is due to the difference between the two drug pairs (1, 2) and (3, 4).