The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design - References
Computational Method
Let 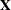 represent the
represent the 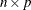 design matrix and
design matrix and 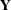 the
the 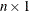 vector of dependent variables. (See the section Parameterization of PROC GLM Models for information about how
vector of dependent variables. (See the section Parameterization of PROC GLM Models for information about how 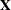 is formed from your model specification.)
is formed from your model specification.)
The normal equations 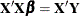 are solved using a modified sweep routine that produces a generalized inverse
are solved using a modified sweep routine that produces a generalized inverse 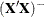 and a solution
and a solution 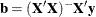 . The modification is that rows and columns corresponding to diagonal elements that are found during sweeping to be zero (or
within the expected level of numerical error of zero) are zeroed out. The
. The modification is that rows and columns corresponding to diagonal elements that are found during sweeping to be zero (or
within the expected level of numerical error of zero) are zeroed out. The 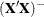 produced by this procedure satisfies the following two equations:
produced by this procedure satisfies the following two equations:
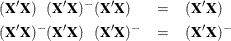
Pringle and Rayner (1971) call a generalized inverse with these characteristics a 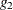 -inverse, and this is the term usually used in SAS documentation and output. Urquhart (1968) uses the term reflexive g-inverse to emphasize that
-inverse, and this is the term usually used in SAS documentation and output. Urquhart (1968) uses the term reflexive g-inverse to emphasize that 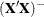 is a generalized inverse of
is a generalized inverse of 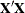 in the same way that
in the same way that 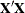 is a generalized inverse of
is a generalized inverse of 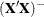 . Note that a
. Note that a 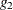 -inverse is not necessarily unique: if
-inverse is not necessarily unique: if 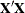 is singular, then sweeping the matrix in a different order will result in a different
is singular, then sweeping the matrix in a different order will result in a different 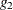 -inverse that also satisfies the two preceding equations.
-inverse that also satisfies the two preceding equations.
For each effect in the model, a matrix  is computed such that the rows of
is computed such that the rows of  are estimable. Tests of the hypothesis
are estimable. Tests of the hypothesis 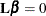 are then made by first computing
are then made by first computing
![\[ \mbox{SS}(\mb{L} \bbeta = 0) = (\mb{Lb})’ (\mb{L}(\mb{X'X})^{-}\mb{L}’)^{-1}(\mb{Lb}) \]](images/statug_glm0360.png)
and then computing the associated F value by using the mean squared error.