The ADAPTIVEREG Procedure

The multivariate adaptive regression splines algorithm is computationally intensive and requires a significant amount of memory for large data sets. However, the core algorithm is fairly scalable, so you might expect performance improvement if you use multicore machines. You can even further improve the fitting speed by carefully tuning the parameters of the FAST option in the MODEL statement.

A general formula does not exist for predicting amount of memory that is required for PROC ADAPTIVEREG. The procedure uses logical utility files to store values that are associated with observations. If sufficient random access memory (RAM) is available, the utility files reside in RAM to allow fast access. Otherwise, the utility files are stored on hard drives, which have slower read/write speed.

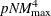Because of the model selection nature, the multivariate adaptive regression splines algorithm essentially fits a large number of candidate models with different sets of basis functions. The original prototype requires computation that is proportional to . The implemented algorithm takes advantage of the special structure of linear truncated power functions to reduce the computation to be proportional to 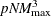. With the fast algorithm, the computations can be reduced even further.

To provide a feel for how the number of variables and the number of observations affect the fitting performance, a series of simulations are carried out on a server with a 12-way 2.6GHz AMD Opteron processor and 32GB of RAM. Data sets are created in different sizes with the number of variables ranging from 10 to 50 and the number of observations ranging from 100 to 5,000. For each data set, the true model is the same as the one used in Example 25.1. At each data size, the experiment is repeated three times to measure minimum running times and corresponding memory consumption. PROC ADAPTIVEREG sets the maximum number of basis function to 50 and uses all other default options. Figure 25.11 displays the results of the simulations.

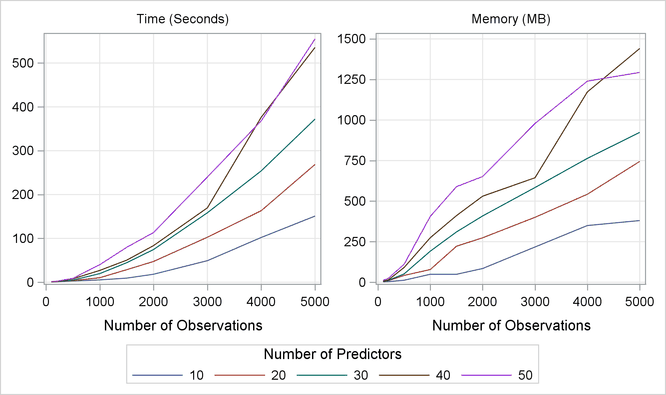
The graphs in Figure 25.11 show that computational times grow with respect to the number of observations at a speed that is slightly faster than linear. The growth of the memory consumption is close to linear. Also, the increment with respect to number of variables is approximately in fixed ratios.

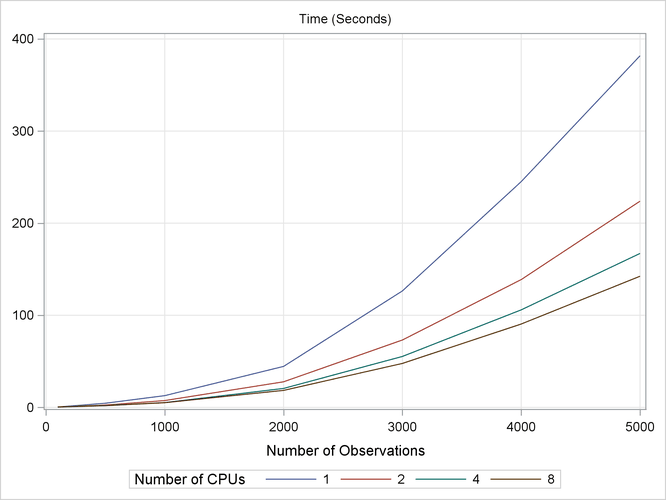
To show how PROC ADAPTIVEREG scales as the number of CPUs grows, another series of experiments is performed with the following settings. SAS DATA steps use the same mechanism as in previous simulations to generate data sets. The number of observations range from 100 to 5,000, and the number of variables is 10. PROC ADAPTIVEREG fits models to these data sets with the maximum number of basis functions set to 50. Each fitting uses four threading settings with 1, 2, 4, and 8 CPUs.

Figure 25.12 displays the simulation results. The computation times scale well with the number of CPUs. The more CPUs you have, the less time you need to fit a model by using PROC ADAPTIVEREG.