The ADAPTIVEREG Procedure
ANOVA Decomposition
The model that is produced by the multivariate adaptive regression splines algorithm can be formed as
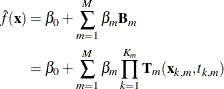
Here 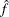 is the nonparametric estimate of the response variable in linear models and of the linked response variable in generalized
linear models. M is the number of nonconstant bases. For each formed basis,
is the nonparametric estimate of the response variable in linear models and of the linked response variable in generalized
linear models. M is the number of nonconstant bases. For each formed basis, 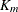 is the order of interaction,
is the order of interaction, 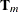 is the variable transformation function that depends on the variable type,
is the variable transformation function that depends on the variable type, 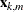 is variable for the kth component of the basis, and
is variable for the kth component of the basis, and 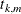 is the corresponding knot value or subset categories for the variable.
is the corresponding knot value or subset categories for the variable.
The function estimate can be recast into the form
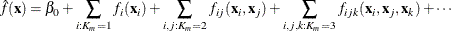
where 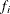 represents the sum of bases that involve a single variable
represents the sum of bases that involve a single variable 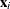 ,
, 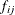 represents the sum of bases that involve two-way interactions between transformations of two variables, and so on. The univariate
function
represents the sum of bases that involve two-way interactions between transformations of two variables, and so on. The univariate
function 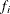 is a linear regression spline for variable
is a linear regression spline for variable 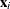 , which represent the univariate contribution of
, which represent the univariate contribution of 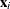 to the model. Let
to the model. Let
![\[ f_{ij}^*=f_ i(\mb{x}_ i)+f_ j(\mb{x}_ j)+f_{ij}(\mb{x}_ i,\mb{x}_ j) \]](images/statug_adaptivereg0113.png)
Then this bivariate function is a tensor product regression spline that represents the joint contribution by both 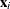 and
and 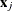 . Multivariate functions can be formed similarly if higher-order interaction terms are present in the model. Because of its
similarity to the analysis of variance for contingency tables, this is referred as the ANOVA decomposition of the multivariate
adaptive regression splines model.
. Multivariate functions can be formed similarly if higher-order interaction terms are present in the model. Because of its
similarity to the analysis of variance for contingency tables, this is referred as the ANOVA decomposition of the multivariate
adaptive regression splines model.
