Example 29.22 Testing Equality of Covariance and Mean Matrices between Independent Groups
To make the specification of some standard MSTRUCT models for covariance and mean patterns more efficient, PROC CALIS defines
these standard models internally. You can use two options to invoke these built-in covariance and mean patterns easily. For
example, with the COVPATTERN= option, you can define the compound symmetry (COMPSYM) pattern for the covariance matrix or the equality of covariance matrices
between groups (EQCOVMAT). With the MEANPATTERN= option, you can define uniform means (UNIFORM) for the mean vector or the equality of mean vectors between groups (EQMEANVEC).
See the COVPATTERN= and the MEANPATTERN= options for details about the supported built-in covariance and mean patterns.
In Example 29.21, you test of the equality of covariance matrices between two groups. This example extends the application to the test of
equality of mean vectors between three independent groups by using the COVPATTERN= and MEANPATTERN= options together. The
“best” fit model for the data is explored. The following DATA steps define the covariance and mean matrices for the three independent
groups, respectively:
data g1(type=corr);
Input _type_ $ 1-8 _name_ $ 9-11 x1-x9;
datalines;
corr x1 1. . . . . . . . .
corr x2 .721 1. . . . . . . .
corr x3 .676 .379 1. . . . . . .
corr x4 .149 .403 .450 1. . . . . .
corr x5 .422 .384 .445 .411 1. . . . .
corr x6 .343 .456 .243 .308 .531 1. . . .
corr x7 .115 .225 .201 .481 .373 .198 1. . .
corr x8 .213 .237 .434 .503 .267 .333 .355 1. .
corr x9 .236 .257 .159 .246 .126 .235 .601 .512 1.
mean . 21.3 22.3 17.2 23.4 22.1 15.6 18.7 20.1 19.7
std . 1.2 1.4 .87 1.33 2.2 1.4 2.3 2.1 1.8
n . 21 21 21 21 21 21 21 21 21
;
data g2(type=corr);
Input _type_ $ 1-8 _name_ $ 9-11 x1-x9;
datalines;
corr x1 1. . . . . . . . .
corr x2 .733 1. . . . . . . .
corr x3 .576 .388 1. . . . . . .
corr x4 .209 .414 .425 1. . . . . .
corr x5 .412 .286 .461 .398 1. . . . .
corr x6 .323 .399 .212 .302 .522 1. . . .
corr x7 .215 .295 .188 .467 .334 .232 1. . .
corr x8 .204 .257 .462 .522 .298 .355 .372 1. .
corr x9 .245 .272 .177 .301 .156 .246 .578 .422 1.
mean . 22.1 19.8 16.9 23.3 21.9 17.3 17.9 19.1 19.8
std . 1.3 1.3 .99 1.25 2.1 1.3 2.2 2.0 1.5
n . 22 22 22 22 22 22 22 22 22
;
data g3(type=corr);
Input _type_ $ 1-8 _name_ $ 9-11 x1-x9;
datalines;
corr x1 1. . . . . . . . .
corr x2 .699 1. . . . . . . .
corr x3 .488 .328 1. . . . . . .
corr x4 .235 .398 .413 1. . . . . .
corr x5 .377 .265 .471 .376 1. . . . .
corr x6 .335 .412 .265 .314 .503 1. . . .
corr x7 .243 .216 .192 .423 .369 .212 1. . .
corr x8 .217 .292 .423 .525 .219 .317 .376 1. .
corr x9 .211 .283 .152 .285 .147 .135 .633 .579 1.
mean . 22.2 20.9 15.4 25.1 22.6 16.3 19.3 20.2 19.5
std . 1.5 1.0 1.04 1.5 1.9 1.6 2.4 2.2 1.6
n . 20 20 20 20 20 20 20 20 20
;
Each of these data sets contains the information about the correlations, means, standard deviations, and sample sizes. Even
though these data sets contain correlations, by default PROC CALIS analyzes the covariances and means.
The first hypothesis to test is the equality of covariance matrices and mean vectors:
where 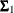 ,
, 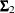 , and
, and 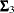 are the population covariance matrices for the three independent groups, respectively, and
are the population covariance matrices for the three independent groups, respectively, and 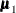 ,
, 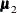 , and
, and 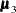 are the population mean vectors for the three independent groups, respectively.
are the population mean vectors for the three independent groups, respectively.
The following statements specify this test:
proc calis covpattern=eqcovmat meanpattern=eqmeanvec;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
In the PROC CALIS statement, the COVPATTERN=EQCOVMAT option specifies the same covariance matrix for the three groups and
the MEANPATTERN=EQMEANVEC option specifies the same mean vector for the three groups. The VAR statement specifies that x1–9 are the variables in the hypothesis test. Next, the GROUP statements specify the data sets for the three independent groups.
You use the FITINDEX statement to limit the amount of output fit statistics to the quantities specified: the chi-square test
(CHISQ), the degrees of freedom (DF), the significance value of the test statistic (PROBCHI), the root mean square error of
approximation (RMSEA), Akaike’s information criterion (AIC), consistent Akaike’s information criterion (CAIC), and Schwarz’s
Bayesian criterion (SBC). The first three quantities are useful for the chi-square model fit test, while the rest of the fit
indices are useful for comparing competing models for the data. Because there are not many quantities in this customized fit
summary table, the NOINDEXTYPE option is used to suppress the printing of the fit index types.
Output 29.22.1 shows the general modeling information, including the sample sizes, the models for the groups, the model types, and the analysis
types.
Output 29.22.1: Modeling Information for Testing Equality of Covariance and Mean Matrices
| WORK.G1 |
21 |
Model 1 |
MSTRUCT |
Means and Covariances |
| WORK.G2 |
22 |
Model 2 |
MSTRUCT |
Means and Covariances |
| WORK.G3 |
20 |
Model 3 |
MSTRUCT |
Means and Covariances |
Output 29.22.2 shows the initial mean vector and the initial covariance matrix specifications for Model 1, which fits to Group 1. PROC CALIS
generates the mean parameter names _mean_1, _mean_2, …, and _mean_9 for the nine elements in the mean vector. It also generates the covariance parameter names _cov_1_1, _cov_2_1, …, and _cov_9_9 for the 45 nonredundant elements in the covariance matrix.
Output 29.22.2: Initial Mean Vector and Covariance Matrix for Model 1
| _mean_1 |
. |
| _mean_2 |
. |
| _mean_3 |
. |
| _mean_4 |
. |
| _mean_5 |
. |
| _mean_6 |
. |
| _mean_7 |
. |
| _mean_8 |
. |
| _mean_9 |
. |
Although not shown here, the initial mean vector and covariance matrices for Models 2 and 3 are exactly the same as those
shown in Output 29.22.2, as required by the equality of covariance and mean matrices in the null hypothesis 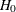 .
.
Output 29.22.3 shows the customized fit summary table. The chi-square test statistic is 203.2605. The degrees of freedom is 108 and the
p-value is less than 0.0001. Therefore, the hypothesis 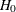 of equality in covariance and mean matrices is rejected for the three independent groups. The RMSEA index is much greater
than 0.05, which does not indicate a good model fit. Other fit indices such as AIC, CAIC, and SBC are not interpreted for
the fit of the model itself, but are useful for comparing competing models in the later discussion.
of equality in covariance and mean matrices is rejected for the three independent groups. The RMSEA index is much greater
than 0.05, which does not indicate a good model fit. Other fit indices such as AIC, CAIC, and SBC are not interpreted for
the fit of the model itself, but are useful for comparing competing models in the later discussion.
Output 29.22.3: Fit Summary for Testing 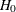 : Equality of Covariance and Mean Matrices
: Equality of Covariance and Mean Matrices
| 203.2605 |
| 108 |
| <.0001 |
| 0.2100 |
| 311.2605 |
| 480.9897 |
| 426.9897 |
A less restrictive hypothesis is now considered. This hypothesis states the equality of covariance matrices only:
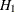 differs from
differs from 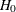 in that the population means in
in that the population means in 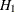 are not constrained. To test this hypothesis, you need to change the MEANPATTERN= option to use the SATURATED keyword, as
shown in the following statements:
are not constrained. To test this hypothesis, you need to change the MEANPATTERN= option to use the SATURATED keyword, as
shown in the following statements:
proc calis covpattern=eqcovmat meanpattern=saturated;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
Output 29.22.4 shows the results of the testing 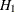 .
.
Output 29.22.4: Fit Summary for Testing 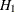 : Equality of Covariance Matrices but Unconstrained Means
: Equality of Covariance Matrices but Unconstrained Means
| 26.7897 |
| 90 |
| 1.0000 |
| 0.0000 |
| 170.7897 |
| 397.0954 |
| 325.0954 |
The chi-square test statistic is 26.7897 (df = 90, p = 1.000). You cannot reject this null hypothesis about the equality of the population covariance matrices. The RMSEA value
is virtually zero, which indicates a perfect fit. Comparing the models under 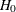 and
and 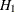 , it is clear that the three groups are significantly different with regard to their mean vectors. By relaxing all the equality
constraints on the means in
, it is clear that the three groups are significantly different with regard to their mean vectors. By relaxing all the equality
constraints on the means in 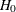 ,
, 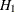 is derived and is supported by the chi-square test. In addition, the RMSEA value for the model under
is derived and is supported by the chi-square test. In addition, the RMSEA value for the model under 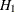 is perfect. Because lower values of AIC, CAIC, and SBC values indicate better model fit (with the model complexity taken
into account), these indices in Output 29.22.3 and Output 29.22.4 support that the model under
is perfect. Because lower values of AIC, CAIC, and SBC values indicate better model fit (with the model complexity taken
into account), these indices in Output 29.22.3 and Output 29.22.4 support that the model under 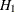 is better than
is better than 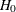 .
.
However, in getting a superior model fit, 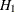 might have relaxed more constraints than absolutely necessary for an optimal fit. That is, it might be possible to impose
equality constraints on only some (but not all, as in
might have relaxed more constraints than absolutely necessary for an optimal fit. That is, it might be possible to impose
equality constraints on only some (but not all, as in 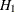 ) of the means to reach the same or even better model fit (by the RMSEA, AIC, CAIC, or SBC criterion) than the model under
) of the means to reach the same or even better model fit (by the RMSEA, AIC, CAIC, or SBC criterion) than the model under
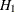 . But how can you determine this set of constrained means?
. But how can you determine this set of constrained means?
To answer this question, you conduct an exploratory analysis of the data by using some model modification techniques. Models
established from exploratory analysis should be validated by external data in the future. However, this example demonstrates
the exploratory part only.
Beginning with the model under 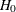 , you can manually take away some particular constraints on the means and explore whether the revised model improves the fit.
If the revised model fits better, you can repeat the process until you cannot improve more. Ultimately, you might be able
to find the “best” model between the models specified under
, you can manually take away some particular constraints on the means and explore whether the revised model improves the fit.
If the revised model fits better, you can repeat the process until you cannot improve more. Ultimately, you might be able
to find the “best” model between the models specified under 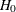 and
and 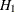 . Such an exploratory analysis is laborious, considering the vast possibilities of constraints on the nine variable means
in three independent groups that you could attempt to release. Fortunately, PROC CALIS provides some model modification statistics,
called the LM (Lagrange multiplier) statistics, to assist this kind of exploratory analysis.
. Such an exploratory analysis is laborious, considering the vast possibilities of constraints on the nine variable means
in three independent groups that you could attempt to release. Fortunately, PROC CALIS provides some model modification statistics,
called the LM (Lagrange multiplier) statistics, to assist this kind of exploratory analysis.
The following statements specify the model under 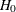 , but now with the MODIFICATION option added to the PROC CALIS statement:
, but now with the MODIFICATION option added to the PROC CALIS statement:
proc calis covpattern=eqcovmat meanpattern=eqmeanvec modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
The MODIFICATION option requests the so-called LM (Lagrange multiplier) statistics for releasing the parameter constraints.
These constraints include the cross-group or within-group constraints and the fixed values in the model. For the model under
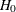 , the covariances and the means are all constrained across groups. These are the equality constraints that you would like
to release to obtain a better model fit. Output 29.22.5 shows the results of the LM statistics for releasing these equality constraints in variances, covariances, and means.
, the covariances and the means are all constrained across groups. These are the equality constraints that you would like
to release to obtain a better model fit. Output 29.22.5 shows the results of the LM statistics for releasing these equality constraints in variances, covariances, and means.
Output 29.22.5: Lagrange Multiplier Statistics for Releasing the Equality Constraints
| 0.01137 |
0.9151 |
0.0178 |
-0.0355 |
| 1.00150 |
0.3169 |
0.1729 |
-0.3212 |
| 1.28632 |
0.2567 |
-0.1818 |
0.3923 |
| 2.19353 |
0.1386 |
0.2038 |
-0.4076 |
| 0.77014 |
0.3802 |
-0.1253 |
0.2327 |
| 0.36128 |
0.5478 |
-0.0796 |
0.1718 |
| 3.12065 |
0.0773 |
-0.4344 |
0.8687 |
| 0.05704 |
0.8112 |
-0.0609 |
0.1132 |
| 4.14151 |
0.0418 |
0.4817 |
-1.0395 |
| 0.00672 |
0.9347 |
0.00888 |
-0.0178 |
| 2.23758 |
0.1347 |
-0.1681 |
0.3122 |
| 2.10455 |
0.1469 |
0.1512 |
-0.3264 |
| 2.18538 |
0.1393 |
-0.1940 |
0.3881 |
| 3.14532 |
0.0761 |
0.2416 |
-0.4487 |
| 0.10264 |
0.7487 |
-0.0405 |
0.0874 |
| 1.56813 |
0.2105 |
0.1815 |
-0.3630 |
| 0.66118 |
0.4161 |
0.1223 |
-0.2272 |
| 4.42160 |
0.0355 |
-0.2934 |
0.6332 |
| 0.31691 |
0.5735 |
-0.0667 |
0.1333 |
| 0.32615 |
0.5679 |
0.0702 |
-0.1304 |
| 0.0002277 |
0.9880 |
-0.00172 |
0.00371 |
| 0.73377 |
0.3917 |
0.1242 |
-0.2484 |
| 0.53196 |
0.4658 |
-0.1097 |
0.2038 |
| 0.01445 |
0.9043 |
-0.0168 |
0.0362 |
| 0.0000258 |
0.9959 |
0.000547 |
-0.00109 |
| 0.24892 |
0.6178 |
-0.0558 |
0.1036 |
| 0.25646 |
0.6126 |
0.0525 |
-0.1134 |
| 0.04412 |
0.8336 |
0.0361 |
-0.0722 |
| 0.52198 |
0.4700 |
0.1288 |
-0.2392 |
| 0.90948 |
0.3403 |
-0.1577 |
0.3403 |
| 0.0008607 |
0.9766 |
-0.00477 |
0.00953 |
| 0.01238 |
0.9114 |
0.0188 |
-0.0348 |
| 0.00712 |
0.9328 |
-0.0132 |
0.0285 |
| 0.10637 |
0.7443 |
-0.0649 |
0.1297 |
| 0.00631 |
0.9367 |
-0.0164 |
0.0304 |
| 0.16971 |
0.6804 |
0.0789 |
-0.1702 |
| 0.06645 |
0.7966 |
-0.0385 |
0.0771 |
| 0.0008275 |
0.9771 |
0.00446 |
-0.00829 |
| 0.05370 |
0.8167 |
0.0334 |
-0.0720 |
| 0.24212 |
0.6227 |
0.0809 |
-0.1617 |
| 0.04459 |
0.8328 |
-0.0360 |
0.0669 |
| 0.07959 |
0.7779 |
-0.0446 |
0.0963 |
| 0.01778 |
0.8939 |
-0.0431 |
0.0862 |
| 0.08223 |
0.7743 |
-0.0962 |
0.1787 |
| 0.18417 |
0.6678 |
0.1336 |
-0.2883 |
| 0.29558 |
0.5867 |
-0.0721 |
0.1442 |
| 0.26589 |
0.6061 |
-0.0710 |
0.1318 |
| 1.16570 |
0.2803 |
0.1378 |
-0.2974 |
| 0.00228 |
0.9619 |
-0.00780 |
0.0156 |
| 1.00319 |
0.3165 |
0.1697 |
-0.3152 |
| 0.95767 |
0.3278 |
-0.1538 |
0.3320 |
| 1.39116 |
0.2382 |
0.1513 |
-0.3027 |
| 0.08741 |
0.7675 |
-0.0394 |
0.0731 |
| 0.79586 |
0.3723 |
-0.1102 |
0.2378 |
| 0.46031 |
0.4975 |
-0.0947 |
0.1894 |
| 0.04254 |
0.8366 |
0.0299 |
-0.0555 |
| 0.22665 |
0.6340 |
0.0640 |
-0.1381 |
| 0.14991 |
0.6986 |
-0.0700 |
0.1399 |
| 0.04723 |
0.8280 |
0.0408 |
-0.0757 |
| 0.02874 |
0.8654 |
0.0295 |
-0.0636 |
| 0.22550 |
0.6349 |
0.1079 |
-0.2158 |
| 0.04390 |
0.8340 |
0.0494 |
-0.0918 |
| 0.48451 |
0.4864 |
-0.1523 |
0.3286 |
| 0.50774 |
0.4761 |
0.1203 |
-0.2406 |
| 0.01246 |
0.9111 |
-0.0196 |
0.0363 |
| 0.36926 |
0.5434 |
-0.0988 |
0.2131 |
| 0.01235 |
0.9115 |
0.0228 |
-0.0455 |
| 0.16400 |
0.6855 |
-0.0861 |
0.1598 |
| 0.09159 |
0.7622 |
0.0597 |
-0.1288 |
| 0.16844 |
0.6815 |
-0.0644 |
0.1288 |
| 0.15095 |
0.6976 |
0.0633 |
-0.1175 |
| 0.0003079 |
0.9860 |
0.00265 |
-0.00572 |
| 0.22542 |
0.6349 |
-0.0776 |
0.1551 |
| 0.00754 |
0.9308 |
0.0147 |
-0.0273 |
| 0.15376 |
0.6950 |
0.0617 |
-0.1331 |
| 0.07831 |
0.7796 |
-0.0631 |
0.1262 |
| 0.07552 |
0.7835 |
0.0643 |
-0.1195 |
| 3.293E-6 |
0.9986 |
0.000394 |
-0.00085 |
| 0.13810 |
0.7102 |
0.0726 |
-0.1452 |
| 0.0001086 |
0.9917 |
0.00211 |
-0.00392 |
| 0.14999 |
0.6985 |
-0.0729 |
0.1572 |
| 0.09334 |
0.7600 |
0.1051 |
-0.2101 |
| 0.00128 |
0.9714 |
0.0128 |
-0.0237 |
| 0.11994 |
0.7291 |
-0.1147 |
0.2474 |
| 0.04800 |
0.8266 |
0.0353 |
-0.0706 |
| 0.19725 |
0.6569 |
0.0743 |
-0.1379 |
| 0.45888 |
0.4981 |
-0.1051 |
0.2268 |
| 0.13689 |
0.7114 |
0.0727 |
-0.1453 |
| 0.31671 |
0.5736 |
-0.1147 |
0.2130 |
| 0.04084 |
0.8398 |
0.0382 |
-0.0825 |
| 0.37615 |
0.5397 |
-0.0904 |
0.1808 |
| 0.00452 |
0.9464 |
-0.0103 |
0.0191 |
| 0.47678 |
0.4899 |
0.0980 |
-0.2114 |
| 0.00989 |
0.9208 |
0.0150 |
-0.0300 |
| 0.01001 |
0.9203 |
0.0157 |
-0.0291 |
| 0.04138 |
0.8388 |
-0.0296 |
0.0638 |
| 0.01378 |
0.9066 |
-0.0267 |
0.0533 |
| 0.03154 |
0.8590 |
-0.0419 |
0.0778 |
| 0.09063 |
0.7634 |
0.0659 |
-0.1421 |
| 0.0007193 |
0.9786 |
0.00510 |
-0.0102 |
| 0.01293 |
0.9095 |
0.0224 |
-0.0417 |
| 0.02067 |
0.8857 |
-0.0263 |
0.0568 |
| 0.16543 |
0.6842 |
0.0952 |
-0.1904 |
| 0.29902 |
0.5845 |
-0.1328 |
0.2467 |
| 0.02206 |
0.8819 |
0.0335 |
-0.0722 |
| 0.00581 |
0.9392 |
0.0244 |
-0.0487 |
| 0.00694 |
0.9336 |
-0.0276 |
0.0513 |
| 0.0000660 |
0.9935 |
0.00250 |
-0.00539 |
| 0.19272 |
0.6607 |
-0.0532 |
0.1063 |
| 0.01910 |
0.8901 |
-0.0174 |
0.0323 |
| 0.34408 |
0.5575 |
0.0684 |
-0.1476 |
| 0.09017 |
0.7640 |
-0.0446 |
0.0892 |
| 0.26496 |
0.6067 |
0.0794 |
-0.1474 |
| 0.04994 |
0.8232 |
-0.0320 |
0.0690 |
| 0.44236 |
0.5060 |
0.0758 |
-0.1516 |
| 0.12761 |
0.7209 |
-0.0422 |
0.0784 |
| 0.09470 |
0.7583 |
-0.0338 |
0.0728 |
| 0.04619 |
0.8298 |
0.0260 |
-0.0520 |
| 0.22996 |
0.6316 |
-0.0602 |
0.1117 |
| 0.07502 |
0.7842 |
0.0319 |
-0.0688 |
| 0.02807 |
0.8669 |
0.0279 |
-0.0557 |
| 0.0006585 |
0.9795 |
-0.00443 |
0.00823 |
| 0.02058 |
0.8859 |
-0.0230 |
0.0496 |
| 0.03989 |
0.8417 |
-0.0282 |
0.0563 |
| 0.15069 |
0.6979 |
-0.0568 |
0.1055 |
| 0.36051 |
0.5482 |
0.0815 |
-0.1759 |
| 0.03398 |
0.8537 |
-0.0284 |
0.0567 |
| 0.05802 |
0.8097 |
0.0385 |
-0.0714 |
| 0.00362 |
0.9520 |
-0.00891 |
0.0192 |
| 0.06050 |
0.8057 |
-0.0391 |
0.0781 |
| 0.56151 |
0.4537 |
0.1235 |
-0.2294 |
| 0.26945 |
0.6037 |
-0.0794 |
0.1713 |
| 0.13296 |
0.7154 |
-0.0655 |
0.1310 |
| 0.00130 |
0.9712 |
-0.00673 |
0.0125 |
| 0.16526 |
0.6844 |
0.0703 |
-0.1517 |
| 11.09173 |
0.0009 |
0.3453 |
-0.6906 |
| 1.21196 |
0.2709 |
-0.1184 |
0.2200 |
| 5.04550 |
0.0247 |
-0.2242 |
0.4838 |
| 21.46921 |
<.0001 |
-0.5837 |
1.1675 |
| 15.27776 |
<.0001 |
0.5110 |
-0.9490 |
| 0.47301 |
0.4916 |
0.0834 |
-0.1800 |
| 4.41967 |
0.0355 |
-0.2034 |
0.4067 |
| 6.37770 |
0.0116 |
-0.2535 |
0.4708 |
| 22.27732 |
<.0001 |
0.4395 |
-0.9485 |
| 3.26860 |
0.0706 |
0.1904 |
-0.3807 |
| 0.03260 |
0.8567 |
0.0197 |
-0.0366 |
| 4.06935 |
0.0437 |
-0.2045 |
0.4413 |
| 0.22210 |
0.6374 |
-0.0681 |
0.1362 |
| 1.50172 |
0.2204 |
0.1837 |
-0.3412 |
| 0.60673 |
0.4360 |
-0.1083 |
0.2338 |
| 1.61486 |
0.2038 |
0.1539 |
-0.3078 |
| 6.72912 |
0.0095 |
-0.3260 |
0.6055 |
| 1.88248 |
0.1701 |
0.1600 |
-0.3452 |
| 0.14035 |
0.7079 |
-0.0558 |
0.1116 |
| 0.11034 |
0.7398 |
0.0514 |
-0.0954 |
| 0.00153 |
0.9688 |
0.00560 |
-0.0121 |
| 0.12603 |
0.7226 |
-0.0510 |
0.1019 |
| 1.96607 |
0.1609 |
0.2089 |
-0.3880 |
| 1.16200 |
0.2811 |
-0.1490 |
0.3215 |
| 0.05301 |
0.8179 |
0.0248 |
-0.0496 |
| 0.97965 |
0.3223 |
-0.1106 |
0.2054 |
| 0.61083 |
0.4345 |
0.0810 |
-0.1748 |
To use the results of this table, you look for parameters that have large LM statistics (in the LM Stat column). Equivalently,
you can look for parameters that have small p-values (in the Pr > ChiSq column). Loosely speaking, an LM statistic estimates the reduction of model fit chi-square statistic
if you release the constraint on the corresponding parameter. The p-value indicates whether the improvement would be significant. Therefore, releasing those parameters with a high LM statistic
and small p-value would be the key to model improvements. Bear in mind that the LM statistics are linear approximations and they might
not be very accurate as estimates of the actual model improvement, which could only be accessed when you refit the model with
the particular constraint released. Nonetheless, the LM statistics could still be very useful because they show which constraints
could potentially improve the model the most.
Output 29.22.5 shows the results from releasing the constraints on the variances and covariances first. Each constrained element of the
covariance matrix has three rows, respectively, for the three models (or groups). For example, the first parameter is _cov_1_1, which is the same variance parameter for x1 in the three models. The first row shows that if you release the variance of x1 in Model 1 from the constraint (while keeping the variances of x1 being constrained between Models 2 and 3), the LM statistic is 0.01127, and the corresponding p-value is 0.9155. This means that the model fit improvement would be very small and so you do not expect a significant model
fit improvement by releasing this constraint. The columns entitled “Changes” show the estimated parameter changes in the original parameters (that is, _cov_1_1 for Models 2 and 3) and in the released parameter (that is, the new parameter for the variance of x1 in Model 1) if you release the corresponding equality constraint. These two “Changes” columns are not very useful for the present purpose.
Looking through the results for the variance and covariance constraints, you can see that almost all the associated p-values are large (that is, as compared with the conventional 0.05 level for significance). Therefore, all these constraints
on variances and covariances would not improve the model fit significantly. In contrast, the constraints on the means show
that several of them could be released for a sizable model fit improvement. The largest LM statistic in the table is the one
for _mean_3 in Model 3. The LM statistic is 22.27678 and its corresponding p-value is less than 0.0001. This means that if the mean of x3 in Model 3 were not constrained with the means of x3 in Models 1 and 2, you would have expected a reduction in the model fit chi-square statistic that is estimated at 22.27678.
Other notable LM statistics are those for _mean_1 in Model 1, _mean_2 in Model 1 or 2, and _mean_6 in Model 2.
Two important points are noted about the use of the LM statistics. First, the LM statistics are not additive. You cannot expect
that the total reduction in model fit chi-square for releasing a particular set of parameter constraints is the sum of the
corresponding LM statistics. Second, once you release a particular constraint and refit the model, the LM statistics in the
revised model might not follow the same pattern as those LM statistics in the original model. Basically, these are due to
the nonlinearity of the fit function and the dependence of the parameter estimates. Therefore, in order to find the best model
for the data, it would be more sensible to adopt a one-at-a-time approach to release the constraints. That is, you release
one constraint at a time and refit the model to see if you can release more constraints to improve the model fit.
According to the results of LM statistics in Output 29.22.5, you first release the constraint on the _mean_3 parameter, which is for the mean of x3 in Model 3. The following statements fit such a model:
proc calis modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
model 1 / group = 1;
mstruct;
matrix _cov_ = cov01-cov45;
matrix _mean_ = mean1-mean9;
model 2 / group = 2;
refmodel 1;
model 3 / group = 3;
refmodel 1;
renameparm mean3=mean3_mdl3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
Because the revised model is no longer a supported built-in MSTRUCT model, you cannot use the MEANPATTERN= or the COVPATTERN=
options any more. Instead, you now use the MSTRUCT modeling language to specify the covariance and mean patterns. Model 1,
which fits to Group 1, is an MSTRUCT model with variance and covariance parameters cov01–cov45 and mean parameters mean1–mean9. Model 2, which fits to Group 2, refers to the specifications of Model 1, as indicated in a REFMODEL statement. Hence, Model
1 and Model 2 are completely constrained in variances, covariances, and means. Model 3, which fits to Group 3, also refers
to the specifications of Model 1, as indicated in another REFMODEL statement. However, the RENAMEPARM statement renames the
parameter mean3 in the reference model (that is, Model 1) to a new name mean3_mdl3. As a results, all variance, covariance, and mean parameters except one in Model 3 are constrained to be the same as those
in Model 1. The mean of x3 in Model 3 is the only parameter that is not constrained with any other parameters. This forms the first revised model from
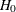 . The MODIFICATION option is specified again to determine whether a further model fit improvement is possible.
. The MODIFICATION option is specified again to determine whether a further model fit improvement is possible.
Output 29.22.6 shows the modeling information of the first revised model. It shows that Models 2 and 3 make references to Model 1. Therefore,
parameters between models are constrained by referencing.
Output 29.22.6: Modeling Information for The First Revised Model
| WORK.G1 |
21 |
Model 1 |
MSTRUCT |
|
Means and Covariances |
| WORK.G2 |
22 |
Model 2 |
MSTRUCT |
Model 1 |
Means and Covariances |
| WORK.G3 |
20 |
Model 3 |
MSTRUCT |
Model 1 |
Means and Covariances |
Output 29.22.7 shows the initial specifications of the means, variances, and covariances in Model 1.
Output 29.22.7: Initial Mean Vector and Covariance Matrix for Model 1 in the First Revised Model
| mean1 |
. |
| mean2 |
. |
| mean3 |
. |
| mean4 |
. |
| mean5 |
. |
| mean6 |
. |
| mean7 |
. |
| mean8 |
. |
| mean9 |
. |
Output 29.22.8 shows the initial specifications of the means in Model 2. The mean parameters in Model 2 are exactly the same as those in
Model 1, as shown in Output 29.22.7. The variance and covariance parameters in Model 2 are also exactly the same as those in Model 1, but are not shown here
to conserve space.
Output 29.22.8: Initial Mean Vector for Model 2 in the First Revised Model
| mean1 |
. |
| mean2 |
. |
| mean3 |
. |
| mean4 |
. |
| mean5 |
. |
| mean6 |
. |
| mean7 |
. |
| mean8 |
. |
| mean9 |
. |
Output 29.22.9 shows the initial specifications of the means in Model 3. All but one mean parameter in Model 3 are exactly the same as those
in Models 1 and 2, as shown in Output 29.22.7 and Output 29.22.8, respectively. The mean for x3 in Model 3 is mean3_mdl3, which is now a distinct parameter, and therefore it is not constrained with any other parameters in the first or the second
models for Groups 1 or 2. However, the variance and covariance parameters in Model 3 are exactly the same as those in Model
1. They are not shown here to conserve space.
Output 29.22.9: Initial Mean Vector for Model 3 in the First Revised Model
| mean1 |
. |
| mean2 |
. |
| mean3_mdl3 |
. |
| mean4 |
. |
| mean5 |
. |
| mean6 |
. |
| mean7 |
. |
| mean8 |
. |
| mean9 |
. |
Output 29.22.10 shows the fit summary of the first revised model. The model fit chi-square is 148.8865, which drops quite a bit from the
original model under 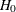 . The p-value of the model fit chi-square is 0.0046, which is statistically significant. The RMSEA value is 0.1399, which is also
a sizable improvement. All the AIC, CAIC, and SBC values are reduced, indicating better model fit than the model under
. The p-value of the model fit chi-square is 0.0046, which is statistically significant. The RMSEA value is 0.1399, which is also
a sizable improvement. All the AIC, CAIC, and SBC values are reduced, indicating better model fit than the model under 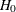 .
.
Output 29.22.10: Fit Summary for the First Revised Model
| 148.8865 |
| 107 |
| 0.0046 |
| 0.1399 |
| 258.8865 |
| 431.7589 |
| 376.7589 |
Output 29.22.11 shows the LM statistics for releasing the equality constraints in the first revised model. Almost all of the results for
the variance and covariance constraints are omitted because their LM statistics are not significant. However, Output 29.22.11 shows all the LM statistics for releasing the constraints in means. The mean of x2 in Model 2 has the largest LM statistic at 26.25044.
Output 29.22.11: LM Statistics for Releasing the Equality Constraints in the First Revised Model
| 0.64999 |
0.4201 |
0.1050 |
-0.2100 |
| 0.41758 |
0.5181 |
0.0874 |
-0.1622 |
| 2.18923 |
0.1390 |
-0.1855 |
0.4004 |
| . |
|
|
|
| . |
|
|
|
| . |
|
|
|
| 9.26674 |
0.0023 |
0.2872 |
-0.5745 |
| 3.00599 |
0.0830 |
-0.1702 |
0.3160 |
| 2.13787 |
0.1437 |
-0.1481 |
0.3196 |
| 26.25115 |
<.0001 |
-0.6568 |
1.3135 |
| 12.34638 |
0.0004 |
0.4674 |
-0.8680 |
| 2.52683 |
0.1119 |
0.1962 |
-0.4234 |
| 0.58891 |
0.4428 |
-0.0787 |
0.0827 |
| 0.58891 |
0.4428 |
0.0827 |
-0.0787 |
| 6.59009 |
0.0103 |
0.2746 |
-0.5493 |
| 0.51343 |
0.4737 |
0.0796 |
-0.1478 |
| 11.61610 |
0.0007 |
-0.3586 |
0.7739 |
| 0.52967 |
0.4667 |
-0.1042 |
0.2084 |
| 0.22294 |
0.6368 |
0.0702 |
-0.1304 |
| 0.06889 |
0.7930 |
0.0374 |
-0.0807 |
| 1.16656 |
0.2801 |
0.1270 |
-0.2540 |
| 5.29599 |
0.0214 |
-0.2810 |
0.5218 |
| 1.69412 |
0.1931 |
0.1518 |
-0.3275 |
| 0.03791 |
0.8456 |
-0.0291 |
0.0582 |
| 0.44510 |
0.5047 |
0.1036 |
-0.1923 |
| 0.23804 |
0.6256 |
-0.0704 |
0.1520 |
| 0.39420 |
0.5301 |
-0.0883 |
0.1765 |
| 0.24231 |
0.6225 |
0.0719 |
-0.1335 |
| 0.01951 |
0.8889 |
0.0200 |
-0.0431 |
| 0.00156 |
0.9685 |
0.00423 |
-0.00846 |
| 1.06866 |
0.3012 |
-0.1150 |
0.2136 |
| 1.05210 |
0.3050 |
0.1065 |
-0.2297 |
You now modify the preceding statements to specify the second revised model, as shown in the following statements:
proc calis modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
model 1 / group = 1;
mstruct;
matrix _cov_ = cov01-cov45;
matrix _mean_ = mean1-mean9;
model 2 / group = 2;
refmodel 1;
renameparm mean2=mean2_new; /* constraint a */
model 3 / group = 3;
refmodel 1;
renameparm mean2=mean2_new, /* constraint a */
mean3=mean3_mdl3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
This second revised model must not constrain the mean of x2 in Model 1 with any parameters. A straightforward way to do this is to rename the mean2 parameter to a unique name in Model 1. However, for the current specification it is more convenient to rename the mean2 parameter in Models 2 and 3 to another name. In the specification of the second revised model, Models 2 and 3 still make
references to Model 1. However, in the respective RENAMEPARM statements, both Model 2 and 3 rename the mean2 parameter that is referenced from Model 1 to the new name mean2_new. This way the mean for x2 in Model 1 is not constrained with the means of x2 in Models 2 and 3. But the means for x2 in Models 2 and 3 are still constrained to be equal by the same parameter mean2_new. Output 29.22.12 shows the fit summary of the second revised model.
Output 29.22.12: Fit Summary for the Second Revised Model
| 86.3927 |
| 106 |
| 0.9183 |
| 0.0000 |
| 198.3927 |
| 374.4083 |
| 318.4083 |
Again, a sizable improvement over the first revised model is shown in the second revised model. The model fit chi-square statistic
is no longer significant (p = 0.9183), and the RMSEA value is perfect at 0. Large drops in the AIC, CAIC, and SBC values are also observed.
Output 29.22.13 suggests that the mean of x6 in Model 2 (which has the largest LM statistic at 11.41243) could be released from the equality constraints to achieve the
largest model improvement over the current model.
Output 29.22.13: LM Statistics for Releasing the Equality Constraints in the Second Revised Model
| 2.77024 |
0.0960 |
0.1384 |
-0.2770 |
| 0.28728 |
0.5920 |
0.0462 |
-0.0860 |
| 5.00087 |
0.0253 |
-0.1791 |
0.3864 |
| . |
|
|
|
| . |
|
|
|
| . |
|
|
|
| 2.75437 |
0.0970 |
0.1646 |
-0.3292 |
| 3.21093 |
0.0731 |
-0.1511 |
0.2806 |
| 0.24923 |
0.6176 |
0.0424 |
-0.0915 |
| 0.74338 |
0.3886 |
-0.0877 |
0.0934 |
| 0.74338 |
0.3886 |
0.0934 |
-0.0877 |
| 6.17449 |
0.0130 |
0.2672 |
-0.5343 |
| 0.02087 |
0.8851 |
-0.0146 |
0.0272 |
| 4.71344 |
0.0299 |
-0.2072 |
0.4470 |
| 1.65517 |
0.1983 |
-0.1853 |
0.3706 |
| 1.16118 |
0.2812 |
0.1606 |
-0.2982 |
| 0.04040 |
0.8407 |
0.0287 |
-0.0618 |
| 5.03834 |
0.0248 |
0.2712 |
-0.5423 |
| 11.41247 |
0.0007 |
-0.4217 |
0.7831 |
| 1.51175 |
0.2189 |
0.1460 |
-0.3150 |
| 0.32382 |
0.5693 |
-0.0853 |
0.1706 |
| 0.82184 |
0.3646 |
0.1410 |
-0.2619 |
| 0.12513 |
0.7235 |
-0.0512 |
0.1104 |
| 2.39207 |
0.1220 |
-0.2210 |
0.4420 |
| 1.58292 |
0.2083 |
0.1867 |
-0.3467 |
| 0.08641 |
0.7688 |
0.0427 |
-0.0922 |
| 0.00682 |
0.9342 |
0.00886 |
-0.0177 |
| 1.20949 |
0.2714 |
-0.1225 |
0.2274 |
| 1.10016 |
0.2942 |
0.1089 |
-0.2349 |
| 4.47814 |
0.0343 |
0.2983 |
-0.2661 |
| 4.47814 |
0.0343 |
-0.2661 |
0.2983 |
The process of model refitting should now become familiar. You modify the previous model to release the constraint on the
mean of x6 in Model 2. As a result, the third revised model is specified by the following statements:
proc calis modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
model 1 / group = 1;
mstruct;
matrix _cov_ = cov01-cov45;
matrix _mean_ = mean1-mean9;
model 2 / group = 2;
refmodel 1;
renameparm mean2=mean2_new, /* constraint a */
mean6=mean6_mdl2;
model 3 / group = 3;
refmodel 1;
renameparm mean2=mean2_new, /* constraint a */
mean3=mean3_mdl3;
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
The only modification from the previous specification is to rename mean6 to mean6_mdl2 in the RENAMEPARM statement of Model 2. Output 29.22.14 shows the model fit summary of the third revised model.
Output 29.22.14: Fit Summary for the Third Revised Model
| 68.7869 |
| 105 |
| 0.9976 |
| 0.0000 |
| 182.7869 |
| 361.9456 |
| 304.9456 |
The model improvement over the second revised model is still notable in the third revised model. The chi-square value drops
about 20 points in the third revised model. The AIC, CAIC, and the SBC values are reduced notably, though not as impressively
as with the previous improvements.
Output 29.22.15 suggests that the mean of x4 in Model 1 (which has the largest LM statistic at 7.01946) could be released from the equality constraint to improve model
fit further.
Output 29.22.15: LM Statistics for Releasing the Equality Constraints in the Third Revised Model
| 2.43374 |
0.1187 |
0.1342 |
-0.2684 |
| 0.19037 |
0.6626 |
0.0390 |
-0.0723 |
| 4.11402 |
0.0425 |
-0.1679 |
0.3625 |
| . |
|
|
|
| . |
|
|
|
| . |
|
|
|
| 6.15722 |
0.0131 |
0.2550 |
-0.5101 |
| 6.05791 |
0.0138 |
-0.2109 |
0.3917 |
| 0.29302 |
0.5883 |
0.0463 |
-0.0999 |
| 2.89780 |
0.0887 |
-0.1796 |
0.1889 |
| 2.89780 |
0.0887 |
0.1889 |
-0.1796 |
| 7.01915 |
0.0081 |
0.2850 |
-0.5701 |
| 0.04916 |
0.8245 |
-0.0226 |
0.0419 |
| 5.05102 |
0.0246 |
-0.2148 |
0.4635 |
| 0.21231 |
0.6450 |
-0.0672 |
0.1345 |
| 0.07502 |
0.7842 |
-0.0443 |
0.0822 |
| 0.55031 |
0.4582 |
0.1059 |
-0.2285 |
| 0.07013 |
0.7911 |
0.0503 |
-0.0486 |
| 0.07013 |
0.7911 |
-0.0486 |
0.0503 |
| 0.98902 |
0.3200 |
-0.1513 |
0.3025 |
| 2.42355 |
0.1195 |
0.2463 |
-0.4575 |
| 0.34231 |
0.5585 |
-0.0858 |
0.1850 |
| 1.58481 |
0.2081 |
-0.1786 |
0.3572 |
| 0.81634 |
0.3663 |
0.1347 |
-0.2502 |
| 0.14503 |
0.7033 |
0.0549 |
-0.1184 |
| 0.13504 |
0.7133 |
0.0399 |
-0.0797 |
| 2.54369 |
0.1107 |
-0.1796 |
0.3335 |
| 1.61681 |
0.2035 |
0.1337 |
-0.2885 |
| 3.21203 |
0.0731 |
0.2484 |
-0.2280 |
| 3.21203 |
0.0731 |
-0.2280 |
0.2484 |
To make the mean parameter for x4 in Model 1 unique, the mean parameters for x4 in Models 2 and 3 are renamed from mean4 to mean4_new, as shown in the following statements:
proc calis modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
model 1 / group = 1;
mstruct;
matrix _cov_ = cov01-cov45;
matrix _mean_ = mean1-mean9;
model 2 / group = 2;
refmodel 1;
renameparm mean2=mean2_new, /* constraint a */
mean4=mean4_new, /* constraint b */
mean6=mean6_mdl2;
model 3 / group = 3;
refmodel 1;
renameparm mean2=mean2_new, /* constraint a */
mean3=mean3_mdl3,
mean4=mean4_new; /* constraint b */
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
This forms the fourth revised model. Output 29.22.16 shows the fit summary of this revised model. Again, the chi-square, AIC, CAIC, and SBC values all show improvements, as compared
with the third revised model. However, the improvements do seem to slow down. For example, the CAIC value drops from 361.95
to the current value at 358.43—a mere 3 points reduction. The SBC value drops from 304.95 to the current value at 300.43—a
mere 4 points reduction. These small reductions indicate that you might soon reach the point that no more model fit improvement
would be possible with additional release of parameter constraints.
Output 29.22.16: Fit Summary for the Fourth Revised Model
| 60.1265 |
| 104 |
| 0.9998 |
| 0.0000 |
| 176.1265 |
| 358.4283 |
| 300.4283 |
Output 29.22.17 suggests that the mean of x1 in Model 1 (which has the largest LM statistic at 6.45785) could be released from the equality constraint to achieve the
largest model improvement over the current model.
Output 29.22.17: LM Statistics for Releasing the Equality Constraints in the Fourth Revised Model
| 2.60531 |
0.1065 |
0.1376 |
-0.2751 |
| 0.28122 |
0.5959 |
0.0469 |
-0.0871 |
| 4.75001 |
0.0293 |
-0.1788 |
0.3859 |
| . |
|
|
|
| . |
|
|
|
| . |
|
|
|
| 6.45761 |
0.0110 |
0.2616 |
-0.5232 |
| 5.00991 |
0.0252 |
-0.1921 |
0.3568 |
| 0.05931 |
0.8076 |
0.0209 |
-0.0452 |
| 1.53300 |
0.2157 |
-0.1298 |
0.1406 |
| 1.53300 |
0.2157 |
0.1406 |
-0.1298 |
| 0.09749 |
0.7549 |
-0.0457 |
0.0913 |
| 0.19688 |
0.6572 |
-0.0716 |
0.1330 |
| 0.56583 |
0.4519 |
0.1071 |
-0.2310 |
| 0.35800 |
0.5496 |
0.1141 |
-0.1113 |
| 0.35800 |
0.5496 |
-0.1113 |
0.1141 |
| 4.53367E-6 |
0.9983 |
0.000350 |
-0.00070 |
| 0.96363 |
0.3263 |
0.1572 |
-0.2920 |
| 1.00890 |
0.3152 |
-0.1486 |
0.3208 |
| 0.20289 |
0.6524 |
-0.0676 |
0.1351 |
| 0.12445 |
0.7243 |
0.0525 |
-0.0974 |
| 0.00590 |
0.9388 |
0.0110 |
-0.0237 |
| 0.05893 |
0.8082 |
-0.0271 |
0.0542 |
| 1.63723 |
0.2007 |
-0.1448 |
0.2689 |
| 2.44241 |
0.1181 |
0.1652 |
-0.3565 |
| 3.05068 |
0.0807 |
0.2396 |
-0.2246 |
| 3.05068 |
0.0807 |
-0.2246 |
0.2396 |
| 1.81983 |
0.1773 |
0.2306 |
-0.2003 |
| 1.81983 |
0.1773 |
-0.2003 |
0.2306 |
To make the mean parameter for x1 in Model 1 unique, the mean parameters for x1 in Models 2 and 3 are renamed from mean1 to mean1_new, as shown in the following statements:
proc calis modification;
var x1-x9;
group 1 / data=g1;
group 2 / data=g2;
group 3 / data=g3;
model 1 / group = 1;
mstruct;
matrix _cov_ = cov01-cov45;
matrix _mean_ = mean1-mean9;
model 2 / group = 2;
refmodel 1;
renameparm mean1=mean1_new, /* constraint c */
mean2=mean2_new, /* constraint a */
mean4=mean4_new, /* constraint b */
mean6=mean6_mdl2;
model 3 / group = 3;
refmodel 1;
renameparm mean1=mean1_new, /* constraint c */
mean2=mean2_new, /* constraint a */
mean3=mean3_mdl3,
mean4=mean4_new; /* constraint b */
fitindex NoIndexType On(only)=[chisq df probchi rmsea aic caic sbc];
run;
This forms the fifth revised model. Output 29.22.18 shows the fit summary of the fifth revised model. Again, the chi-square, AIC, CAIC, and SBC values all show improvements,
as compared with the fourth revised model. However, the improvements slow down even more. For example, the CAIC value drops
from 358.43 to the current value at 356.32. The SBC value drops from 300.43 to the current value at 297.32. Because the model
fit does not improve much, this is the point where you would cease to release more equality constraints for improving the
model fit.
Output 29.22.18: Fit Summary for the Fifth Revised Model
| 52.8821 |
| 103 |
| 1.0000 |
| 0.0000 |
| 170.8821 |
| 356.3270 |
| 297.3270 |
Output 29.22.19 does not suggest the release of any equality constraints on the means, because all the p-values for the LM statistics are not significant (that is, all are greater than 0.05). Therefore, the same suggestion from
examining the model fit improvements of the fifth revised model echoes here: this is the point that the “best” model for the data is found.
Output 29.22.19: LM Statistics for Releasing the Equality Constraints in the Fifth Revised Model
| 4.06279 |
0.0438 |
0.1590 |
-0.3180 |
| 0.48735 |
0.4851 |
0.0571 |
-0.1061 |
| 7.60892 |
0.0058 |
-0.2095 |
0.4520 |
| . |
|
|
|
| . |
|
|
|
| . |
|
|
|
| 0.08363 |
0.7724 |
-0.0312 |
0.0382 |
| 0.08363 |
0.7724 |
0.0382 |
-0.0312 |
| 0.02394 |
0.8770 |
0.0229 |
-0.0458 |
| 0.47076 |
0.4926 |
-0.1113 |
0.2067 |
| 0.26015 |
0.6100 |
0.0728 |
-0.1571 |
| 0.97521 |
0.3234 |
0.1893 |
-0.1892 |
| 0.97521 |
0.3234 |
-0.1892 |
0.1893 |
| 0.03746 |
0.8465 |
-0.0319 |
0.0638 |
| 1.10428 |
0.2933 |
0.1683 |
-0.3126 |
| 0.79474 |
0.3727 |
-0.1321 |
0.2851 |
| 0.86792 |
0.3515 |
-0.1426 |
0.2852 |
| 0.47493 |
0.4907 |
0.1038 |
-0.1928 |
| 0.03722 |
0.8470 |
0.0276 |
-0.0595 |
| 0.12190 |
0.7270 |
0.0401 |
-0.0801 |
| 2.66768 |
0.1024 |
-0.1869 |
0.3472 |
| 1.78114 |
0.1820 |
0.1417 |
-0.3058 |
| 1.28034 |
0.2578 |
-0.1794 |
0.1359 |
| 1.28034 |
0.2578 |
0.1359 |
-0.1794 |
| 2.53131 |
0.1116 |
0.2117 |
-0.2112 |
| 2.53131 |
0.1116 |
-0.2112 |
0.2117 |
| 2.25832 |
0.1329 |
0.2558 |
-0.2253 |
| 2.25832 |
0.1329 |
-0.2253 |
0.2558 |
To see where the fifth revised model (equality in the covariance matrix and partial equality in the means) stands between
the models under 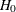 (equality in the covariance and mean matrices) and
(equality in the covariance and mean matrices) and 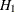 (equality in the covariance matrix only), the following table shows the fit statistics of these three models:
(equality in the covariance matrix only), the following table shows the fit statistics of these three models:
| |
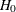
|
“Fifth”
|
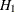
|
|
Chi-square
|
203.2605
|
52.8821
|
26.7897
|
|
Chi-square DF
|
108
|
103
|
90
|
|
Pr > chi-square
|
<0.0001
|
1.0000
|
1.0000
|
|
RMSEA estimate
|
0.2100
|
0.0000
|
0.0000
|
|
Akaike information criterion
|
311.2605
|
170.8821
|
170.7897
|
|
Bozdogan CAIC
|
480.9898
|
356.3270
|
397.0954
|
|
Schwarz Bayesian criterion
|
426.9898
|
297.3270
|
325.0954
|
The fifth revised model is labeled “Fifth” in the table. Compared with the model under 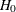 , the fifth revised model is clearly superior. It uses only five more parameters (or five fewer degrees of freedom), but the
improvement in the model fit chi-square and the RMSEA value are huge. The AIC, CAIC, and SBC are also much better.
, the fifth revised model is clearly superior. It uses only five more parameters (or five fewer degrees of freedom), but the
improvement in the model fit chi-square and the RMSEA value are huge. The AIC, CAIC, and SBC are also much better.
Compared with the model under 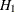 , the fifth revised model appears to be inferior in only the chi-square model fit statistic, although both models already
have the highest possible p-value at 1.000 and smallest possible RMSEA value at 0. However, the model under
, the fifth revised model appears to be inferior in only the chi-square model fit statistic, although both models already
have the highest possible p-value at 1.000 and smallest possible RMSEA value at 0. However, the model under 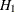 uses 13 more parameters (or it has 13 fewer degrees of freedom), and hence it is more complex. In fact, because the model
fit chi-square value does not take model complexity into account, it is often criticized as the basis for choosing competing
models for the data. In contrast, the AIC, CAIC, and SBC measures take model complexity into account, and they are more reasonable
as the basis for choosing competing models. Although the AIC values for the fifth revised model and the model under
uses 13 more parameters (or it has 13 fewer degrees of freedom), and hence it is more complex. In fact, because the model
fit chi-square value does not take model complexity into account, it is often criticized as the basis for choosing competing
models for the data. In contrast, the AIC, CAIC, and SBC measures take model complexity into account, and they are more reasonable
as the basis for choosing competing models. Although the AIC values for the fifth revised model and the model under 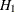 are very close, the CAIC and SBC values clearly favor the fifth revised model. Therefore, according to the CAIC and SBC criteria,
the fifth revised model, which is a model with partial equality constraints on the means, is actually better than the model
with all the means being unconstrained (that is, under
are very close, the CAIC and SBC values clearly favor the fifth revised model. Therefore, according to the CAIC and SBC criteria,
the fifth revised model, which is a model with partial equality constraints on the means, is actually better than the model
with all the means being unconstrained (that is, under 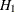 ) for the current data with three independent groups.
) for the current data with three independent groups.


 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis![]() ,
, ![]() , and
, and ![]() are the population covariance matrices for the three independent groups, respectively, and
are the population covariance matrices for the three independent groups, respectively, and ![]() ,
, ![]() , and
, and ![]() are the population mean vectors for the three independent groups, respectively.
are the population mean vectors for the three independent groups, respectively.
![]() .
.
![]() of equality in covariance and mean matrices is rejected for the three independent groups. The RMSEA index is much greater
than 0.05, which does not indicate a good model fit. Other fit indices such as AIC, CAIC, and SBC are not interpreted for
the fit of the model itself, but are useful for comparing competing models in the later discussion.
of equality in covariance and mean matrices is rejected for the three independent groups. The RMSEA index is much greater
than 0.05, which does not indicate a good model fit. Other fit indices such as AIC, CAIC, and SBC are not interpreted for
the fit of the model itself, but are useful for comparing competing models in the later discussion.
![]() : Equality of Covariance and Mean Matrices
: Equality of Covariance and Mean Matrices
![]() differs from
differs from ![]() in that the population means in
in that the population means in ![]() are not constrained. To test this hypothesis, you need to change the MEANPATTERN= option to use the SATURATED keyword, as
shown in the following statements:
are not constrained. To test this hypothesis, you need to change the MEANPATTERN= option to use the SATURATED keyword, as
shown in the following statements:
![]() .
.
![]() : Equality of Covariance Matrices but Unconstrained Means
: Equality of Covariance Matrices but Unconstrained Means
![]() and
and ![]() , it is clear that the three groups are significantly different with regard to their mean vectors. By relaxing all the equality
constraints on the means in
, it is clear that the three groups are significantly different with regard to their mean vectors. By relaxing all the equality
constraints on the means in ![]() ,
, ![]() is derived and is supported by the chi-square test. In addition, the RMSEA value for the model under
is derived and is supported by the chi-square test. In addition, the RMSEA value for the model under ![]() is perfect. Because lower values of AIC, CAIC, and SBC values indicate better model fit (with the model complexity taken
into account), these indices in Output 29.22.3 and Output 29.22.4 support that the model under
is perfect. Because lower values of AIC, CAIC, and SBC values indicate better model fit (with the model complexity taken
into account), these indices in Output 29.22.3 and Output 29.22.4 support that the model under ![]() is better than
is better than ![]() .
.
![]() might have relaxed more constraints than absolutely necessary for an optimal fit. That is, it might be possible to impose
equality constraints on only some (but not all, as in
might have relaxed more constraints than absolutely necessary for an optimal fit. That is, it might be possible to impose
equality constraints on only some (but not all, as in ![]() ) of the means to reach the same or even better model fit (by the RMSEA, AIC, CAIC, or SBC criterion) than the model under
) of the means to reach the same or even better model fit (by the RMSEA, AIC, CAIC, or SBC criterion) than the model under
![]() . But how can you determine this set of constrained means?
. But how can you determine this set of constrained means?
![]() , you can manually take away some particular constraints on the means and explore whether the revised model improves the fit.
If the revised model fits better, you can repeat the process until you cannot improve more. Ultimately, you might be able
to find the “best” model between the models specified under
, you can manually take away some particular constraints on the means and explore whether the revised model improves the fit.
If the revised model fits better, you can repeat the process until you cannot improve more. Ultimately, you might be able
to find the “best” model between the models specified under ![]() and
and ![]() . Such an exploratory analysis is laborious, considering the vast possibilities of constraints on the nine variable means
in three independent groups that you could attempt to release. Fortunately, PROC CALIS provides some model modification statistics,
called the LM (Lagrange multiplier) statistics, to assist this kind of exploratory analysis.
. Such an exploratory analysis is laborious, considering the vast possibilities of constraints on the nine variable means
in three independent groups that you could attempt to release. Fortunately, PROC CALIS provides some model modification statistics,
called the LM (Lagrange multiplier) statistics, to assist this kind of exploratory analysis.
![]() , but now with the MODIFICATION option added to the PROC CALIS statement:
, but now with the MODIFICATION option added to the PROC CALIS statement:
![]() , the covariances and the means are all constrained across groups. These are the equality constraints that you would like
to release to obtain a better model fit. Output 29.22.5 shows the results of the LM statistics for releasing these equality constraints in variances, covariances, and means.
, the covariances and the means are all constrained across groups. These are the equality constraints that you would like
to release to obtain a better model fit. Output 29.22.5 shows the results of the LM statistics for releasing these equality constraints in variances, covariances, and means.
![]() . The MODIFICATION option is specified again to determine whether a further model fit improvement is possible.
. The MODIFICATION option is specified again to determine whether a further model fit improvement is possible.
![]() . The p-value of the model fit chi-square is 0.0046, which is statistically significant. The RMSEA value is 0.1399, which is also
a sizable improvement. All the AIC, CAIC, and SBC values are reduced, indicating better model fit than the model under
. The p-value of the model fit chi-square is 0.0046, which is statistically significant. The RMSEA value is 0.1399, which is also
a sizable improvement. All the AIC, CAIC, and SBC values are reduced, indicating better model fit than the model under ![]() .
.
![]() (equality in the covariance and mean matrices) and
(equality in the covariance and mean matrices) and ![]() (equality in the covariance matrix only), the following table shows the fit statistics of these three models:
(equality in the covariance matrix only), the following table shows the fit statistics of these three models:
![]() , the fifth revised model is clearly superior. It uses only five more parameters (or five fewer degrees of freedom), but the
improvement in the model fit chi-square and the RMSEA value are huge. The AIC, CAIC, and SBC are also much better.
, the fifth revised model is clearly superior. It uses only five more parameters (or five fewer degrees of freedom), but the
improvement in the model fit chi-square and the RMSEA value are huge. The AIC, CAIC, and SBC are also much better.
![]() , the fifth revised model appears to be inferior in only the chi-square model fit statistic, although both models already
have the highest possible p-value at 1.000 and smallest possible RMSEA value at 0. However, the model under
, the fifth revised model appears to be inferior in only the chi-square model fit statistic, although both models already
have the highest possible p-value at 1.000 and smallest possible RMSEA value at 0. However, the model under ![]() uses 13 more parameters (or it has 13 fewer degrees of freedom), and hence it is more complex. In fact, because the model
fit chi-square value does not take model complexity into account, it is often criticized as the basis for choosing competing
models for the data. In contrast, the AIC, CAIC, and SBC measures take model complexity into account, and they are more reasonable
as the basis for choosing competing models. Although the AIC values for the fifth revised model and the model under
uses 13 more parameters (or it has 13 fewer degrees of freedom), and hence it is more complex. In fact, because the model
fit chi-square value does not take model complexity into account, it is often criticized as the basis for choosing competing
models for the data. In contrast, the AIC, CAIC, and SBC measures take model complexity into account, and they are more reasonable
as the basis for choosing competing models. Although the AIC values for the fifth revised model and the model under ![]() are very close, the CAIC and SBC values clearly favor the fifth revised model. Therefore, according to the CAIC and SBC criteria,
the fifth revised model, which is a model with partial equality constraints on the means, is actually better than the model
with all the means being unconstrained (that is, under
are very close, the CAIC and SBC values clearly favor the fifth revised model. Therefore, according to the CAIC and SBC criteria,
the fifth revised model, which is a model with partial equality constraints on the means, is actually better than the model
with all the means being unconstrained (that is, under ![]() ) for the current data with three independent groups.
) for the current data with three independent groups.