Analyses in the ONESAMPLEMEANS Statement :: SAS/STAT(R) 12.3 User's Guide

One-Sample t Test (TEST=T)

The hypotheses for the one-sample t test are

$\displaystyle H_{0}\colon$	$\displaystyle \mu =\mu _0$
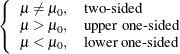$\displaystyle H_{1}\colon$	$\displaystyle \left\{ \begin{array}{ll} \mu \ne \mu _0, & \mbox{two-sided} \\ \mu > \mu _0, & \mbox{upper one-sided} \\ \mu < \mu _0, & \mbox{lower one-sided} \\ \end{array} \right.$

The test assumes normally distributed data and requires $N \ge 2$ . The test statistics are

$\displaystyle t$	$\displaystyle = N^\frac {1}{2} \left( \frac{\bar{x}-\mu _0}{s} \right) \quad \thicksim \; \; t(N-1, \delta )$
$\displaystyle t^2$	$\displaystyle \thicksim F(1, N-1, \delta ^2)$

where $\bar{x}$ is the sample mean, s is the sample standard deviation, and

$\delta = N^\frac {1}{2} \left( \frac{\mu -\mu _0}{\sigma } \right)$

The test is

$\mbox{Reject} \quad H_0 \quad \mbox{if} \left\{ \begin{array}{ll} t^2 \ge F_{1-\alpha }(1, N-1), & \mbox{two-sided} \\ t \ge t_{1-\alpha }(N-1), & \mbox{upper one-sided} \\ t \le t_{\alpha }(N-1), & \mbox{lower one-sided} \\ \end{array} \right.$

Exact power computations for t tests are discussed in O’Brien and Muller (1993, Section 8.2), although not specifically for the one-sample case. The power is based on the noncentral t and F distributions:

$\displaystyle \mr {power}$

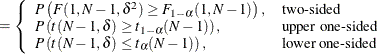$\displaystyle = \left\{ \begin{array}{ll} P\left(F(1, N-1, \delta ^2) \ge F_{1-\alpha }(1, N-1)\right), & \mbox{two-sided} \\ P\left(t(N-1, \delta ) \ge t_{1-\alpha }(N-1)\right), & \mbox{upper one-sided} \\ P\left(t(N-1, \delta ) \le t_{\alpha }(N-1)\right), & \mbox{lower one-sided} \\ \end{array} \right.$

Solutions for N, $\alpha$ , and $\delta$ are obtained by numerically inverting the power equation. Closed-form solutions for other parameters, in terms of $\delta$ , are as follows:

$\displaystyle \mu$	$\displaystyle = \delta \sigma N^{-\frac{1}{2}} + \mu _0$
$\displaystyle \sigma$	$\displaystyle = \left\{ \begin{array}{ll} \delta ^{-1} N^\frac {1}{2} (\mu - \mu _0), & \|\delta \| > 0 \\ \mbox{undefined}, & \mbox{otherwise} \\ \end{array} \right.$

One-Sample t Test with Lognormal Data (TEST=T DIST=LOGNORMAL)

The lognormal case is handled by reexpressing the analysis equivalently as a normality-based test on the log-transformed data, by using properties of the lognormal distribution as discussed in Johnson, Kotz, and Balakrishnan (1994, Chapter 14). The approaches in the section One-Sample t Test (TEST=T) then apply.

In contrast to the usual t test on normal data, the hypotheses with lognormal data are defined in terms of geometric means rather than arithmetic means. This is because the transformation of a null arithmetic mean of lognormal data to the normal scale depends on the unknown coefficient of variation, resulting in an ill-defined hypothesis on the log-transformed data. Geometric means transform cleanly and are more natural for lognormal data.

The hypotheses for the one-sample t test with lognormal data are

$\displaystyle H_{0}\colon$	$\displaystyle \frac{\gamma }{\gamma _0} = 1$
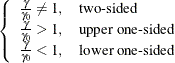$\displaystyle H_{1}\colon$	$\displaystyle \left\{ \begin{array}{ll} \frac{\gamma }{\gamma _0} \ne 1, & \mbox{two-sided} \\ \frac{\gamma }{\gamma _0} > 1, & \mbox{upper one-sided} \\ \frac{\gamma }{\gamma _0} < 1, & \mbox{lower one-sided} \\ \end{array} \right.$

Let $\mu ^\star$ and $\sigma ^\star$ be the (arithmetic) mean and standard deviation of the normal distribution of the log-transformed data. The hypotheses can be rewritten as follows:

$\displaystyle H_{0}\colon$	$\displaystyle \mu ^\star =\log (\gamma _0)$
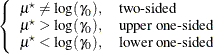$\displaystyle H_{1}\colon$	$\displaystyle \left\{ \begin{array}{ll} \mu ^\star \ne \log (\gamma _0), & \mbox{two-sided} \\ \mu ^\star > \log (\gamma _0), & \mbox{upper one-sided} \\ \mu ^\star < \log (\gamma _0), & \mbox{lower one-sided} \\ \end{array} \right.$

where $\mu ^\star = \log (\gamma )$ .

The test assumes lognormally distributed data and requires $N \ge 2$ .

The power is

$\mr {power} = \left\{ \begin{array}{ll} P\left(F(1, N-1, \delta ^2) \ge F_{1-\alpha }(1, N-1)\right), & \mbox{two-sided} \\ P\left(t(N-1, \delta ) \ge t_{1-\alpha }(N-1)\right), & \mbox{upper one-sided} \\ P\left(t(N-1, \delta ) \le t_{\alpha }(N-1)\right), & \mbox{lower one-sided} \\ \end{array} \right.$

where

$\displaystyle \delta$	$\displaystyle = N^\frac {1}{2} \left( \frac{\mu ^\star - \log (\gamma _0)}{\sigma ^\star } \right)$
$\displaystyle \sigma ^\star$	$\displaystyle = \left[ \log (\mr {CV}^2 + 1) \right]^\frac {1}{2}$

Equivalence Test for Mean of Normal Data (TEST=EQUIV DIST=NORMAL)

The hypotheses for the equivalence test are

$\displaystyle H_{0}\colon$	$\displaystyle \mu < \theta _ L \quad \mbox{or}\quad \mu > \theta _ U$
$\displaystyle H_{1}\colon$	$\displaystyle \theta _ L \le \mu \le \theta _ U$

The analysis is the two one-sided tests (TOST) procedure of Schuirmann (1987). The test assumes normally distributed data and requires $N \ge 2$ . Phillips (1990) derives an expression for the exact power assuming a two-sample balanced design; the results are easily adapted to a one-sample design:

$\displaystyle \mr {power}$	$\displaystyle = Q_{N-1}\left((-t_{1-\alpha }(N-1)),\frac{\mu -\theta _ U}{\sigma N^{-\frac{1}{2}}};0,\frac{(N-1)^\frac {1}{2}(\theta _ U-\theta _ L)}{2\sigma N^{-\frac{1}{2}}(t_{1-\alpha }(N-1))}\right) -$
$\displaystyle$	$\displaystyle \quad Q_{N-1}\left((t_{1-\alpha }(N-1)),\frac{\mu -\theta _ L}{\sigma N^{-\frac{1}{2}}};0,\frac{(N-1)^\frac {1}{2}(\theta _ U-\theta _ L)}{2\sigma N^{-\frac{1}{2}}(t_{1-\alpha }(N-1))}\right)$

where $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

Equivalence Test for Mean of Lognormal Data (TEST=EQUIV DIST=LOGNORMAL)

The lognormal case is handled by reexpressing the analysis equivalently as a normality-based test on the log-transformed data, by using properties of the lognormal distribution as discussed in Johnson, Kotz, and Balakrishnan (1994, Chapter 14). The approaches in the section Equivalence Test for Mean of Normal Data (TEST=EQUIV DIST=NORMAL) then apply.

In contrast to the additive equivalence test on normal data, the hypotheses with lognormal data are defined in terms of geometric means rather than arithmetic means. This is because the transformation of an arithmetic mean of lognormal data to the normal scale depends on the unknown coefficient of variation, resulting in an ill-defined hypothesis on the log-transformed data. Geometric means transform cleanly and are more natural for lognormal data.

The hypotheses for the equivalence test are

$\displaystyle H_{0}\colon$	$\displaystyle \gamma \le \theta _ L \quad \mbox{or}\quad \gamma \ge \theta _ U$
$\displaystyle H_{1}\colon$	$\displaystyle \theta _ L < \gamma < \theta _ U$

$\mbox{where}\quad 0 < \theta _ L < \theta _ U$

The analysis is the two one-sided tests (TOST) procedure of Schuirmann (1987) on the log-transformed data. The test assumes lognormally distributed data and requires $N \ge 2$ . Diletti, Hauschke, and Steinijans (1991) derive an expression for the exact power assuming a crossover design; the results are easily adapted to a one-sample design:

$\displaystyle \mr {power}$	$\displaystyle = Q_{N-1}\left((-t_{1-\alpha }(N-1)),\frac{\log \left(\gamma \right)-\log (\theta _ U)}{\sigma ^\star N^{-\frac{1}{2}}}; 0,\frac{(N-1)^\frac {1}{2}(\log (\theta _ U)-\log (\theta _ L))}{2\sigma ^\star N^{-\frac{1}{2}}(t_{1-\alpha }(N-1))}\right) -$
$\displaystyle$	$\displaystyle \quad Q_{N-1}\left((t_{1-\alpha }(N-1)),\frac{\log \left(\gamma \right)-\log (\theta _ L)}{\sigma ^\star N^{-\frac{1}{2}}}; 0,\frac{(N-1)^\frac {1}{2}(\log (\theta _ U)-\log (\theta _ L))}{2\sigma ^\star N^{-\frac{1}{2}}(t_{1-\alpha }(N-1))}\right)$

where

$\sigma ^\star = \left[ \log (\mr {CV}^2+1) \right]^\frac {1}{2}$

is the standard deviation of the log-transformed data, and $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

Confidence Interval for Mean (CI=T)

This analysis of precision applies to the standard t-based confidence interval:

$\begin{array}{ll} \left[ \bar{x} - t_{1-\frac{\alpha }{2}}(N-1) \frac{s}{\sqrt {N}}, \quad \bar{x} + t_{1-\frac{\alpha }{2}}(N-1) \frac{s}{\sqrt {N}} \right], & \mbox{two-sided} \\ \left[ \bar{x} - t_{1-\alpha }(N-1) \frac{s}{\sqrt {N}}, \quad \infty \right), & \mbox{upper one-sided} \\ \left( -\infty , \quad \bar{x} + t_{1-\alpha }(N-1) \frac{s}{\sqrt {N}} \right], & \mbox{lower one-sided} \\ \end{array}$

where $\bar{x}$ is the sample mean and s is the sample standard deviation. The “half-width” is defined as the distance from the point estimate $\bar{x}$ to a finite endpoint,

$\mbox{half-width} = \left\{ \begin{array}{ll} t_{1-\frac{\alpha }{2}}(N-1) \frac{s}{\sqrt {N}}, & \mbox{two-sided} \\ t_{1-\alpha }(N-1) \frac{s}{\sqrt {N}}, & \mbox{one-sided} \\ \end{array} \right.$

A “valid” conference interval captures the true mean. The exact probability of obtaining at most the target confidence interval half-width h, unconditional or conditional on validity, is given by Beal (1989):

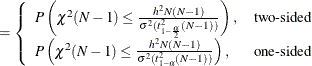$\displaystyle \mbox{Pr(half-width $\le h$)}$	$\displaystyle = \left\{ \begin{array}{ll} P\left( \chi ^2(N-1) \le \frac{h^2N(N-1)}{\sigma ^2 (t^2_{1-\frac{\alpha }{2}}(N-1))} \right), & \mbox{two-sided} \\ P\left( \chi ^2(N-1) \le \frac{h^2N(N-1)}{\sigma ^2 (t^2_{1-\alpha }(N-1))} \right), & \mbox{one-sided} \\ \end{array} \right.$
$\displaystyle \begin{array}{r} \mbox{Pr(half-width $\le h$ \|} \\ \mbox{validity)} \end{array}$	$\displaystyle = \left\{ \begin{array}{ll} \left(\frac{1}{1-\alpha }\right) 2 \left[ Q_{N-1}\left((t_{1-\frac{\alpha }{2}}(N-1)),0; \right. \right. \\ \quad \left. \left. 0,b_1\right) - Q_{N-1}(0,0;0,b_1)\right], & \mbox{two-sided} \\ \left(\frac{1}{1-\alpha }\right) Q_{N-1}\left((t_{1-\alpha }(N-1)),0;0,b_1\right), & \mbox{one-sided} \\ \end{array} \right.$

where

$\displaystyle b_1$	$\displaystyle = \frac{h(N-1)^\frac {1}{2}}{\sigma (t_{1-\frac{\alpha }{c}}(N-1))N^{-\frac{1}{2}}}$
$\displaystyle c$	$\displaystyle = \mbox{number of sides}$

and $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

A “quality” confidence interval is both sufficiently narrow (half-width $\le h$ ) and valid:

$\displaystyle \mbox{Pr(quality)}$	$\displaystyle = \mbox{Pr(half-width $\le h$ and validity)}$
$\displaystyle$	$\displaystyle = \mbox{Pr(half-width $\le h$ \| validity)($1-\alpha $)}$

The POWER Procedure

Analyses in the ONESAMPLEMEANS Statement

One-Sample t Test (TEST=T)

One-Sample t Test with Lognormal Data (TEST=T DIST=LOGNORMAL)

Equivalence Test for Mean of Normal Data (TEST=EQUIV DIST=NORMAL)

Equivalence Test for Mean of Lognormal Data (TEST=EQUIV DIST=LOGNORMAL)

Confidence Interval for Mean (CI=T)