The POWER Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test
One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test - References
Let X be distributed as ![]() . The hypotheses for the test of the proportion p are as follows:
. The hypotheses for the test of the proportion p are as follows:
|
|
|
|
|
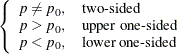 |
The exact test assumes binomially distributed data and requires ![]() and
and ![]() . The test statistic is
. The test statistic is
The significance probability ![]() is split symmetrically for two-sided tests, in the sense that each tail is filled with as much as possible up to
is split symmetrically for two-sided tests, in the sense that each tail is filled with as much as possible up to ![]() .
.
Exact power computations are based on the binomial distribution and computing formulas such as the following from Johnson, Kotz, and Kemp (1992, equation 3.20):
Let ![]() and
and ![]() denote lower and upper critical values, respectively. Let
denote lower and upper critical values, respectively. Let ![]() denote the achieved (actual) significance level, which for two-sided tests is the sum of the favorable major tail (
denote the achieved (actual) significance level, which for two-sided tests is the sum of the favorable major tail (![]() ) and the opposite minor tail (
) and the opposite minor tail (![]() ).
).
For the upper one-sided case,
|
|
|
|
|
|
|
|
|
|
|
|
For the lower one-sided case,
|
|
|
|
|
|
|
|
|
|
|
|
For the two-sided case,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For the normal approximation test, the test statistic is
For the METHOD=EXACT option, the computations are the same as described in the section Exact Test of a Binomial Proportion (TEST=EXACT) except for the definitions of the critical values.
For the upper one-sided case,
|
|
|
For the lower one-sided case,
|
|
|
For the two-sided case,
|
|
|
|
|
|
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
The approximate power is computed as
|
|
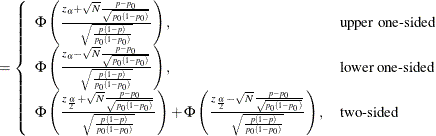 |
The approximate sample size is computed in closed form for the one-sided cases by inverting the power equation,
and by numerical inversion for the two-sided case.
For the normal approximation test using the sample variance, the test statistic is
where ![]() .
.
For the METHOD=EXACT option, the computations are the same as described in the section Exact Test of a Binomial Proportion (TEST=EXACT) except for the definitions of the critical values.
For the upper one-sided case,
|
|
|
For the lower one-sided case,
|
|
|
For the two-sided case,
|
|
|
|
|
|
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
(see Chow, Shao, and Wang (2003, p. 82)).
The approximate power is computed as
|
|
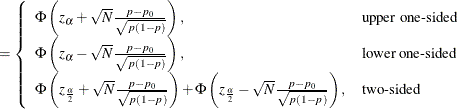 |
The approximate sample size is computed in closed form for the one-sided cases by inverting the power equation,
and by numerical inversion for the two-sided case.
For the normal approximation test with continuity adjustment, the test statistic is (Pagano and Gauvreau, 1993, p. 295):
For the METHOD=EXACT option, the computations are the same as described in the section Exact Test of a Binomial Proportion (TEST=EXACT) except for the definitions of the critical values.
For the upper one-sided case,
|
|
|
For the lower one-sided case,
|
|
|
For the two-sided case,
|
|
|
|
|
|
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , where
, where ![]() and
and ![]() are derived as follows.
are derived as follows.
For convenience of notation, define
Then
and
|
|
|
|
|
|
The probabilities ![]() ,
, ![]() , and
, and ![]() and the truncated expectations
and the truncated expectations ![]() and
and ![]() are approximated by assuming the normal-approximate distribution of X,
are approximated by assuming the normal-approximate distribution of X, ![]() . Letting
. Letting ![]() and
and ![]() denote the standard normal PDF and CDF, respectively, and defining d as
denote the standard normal PDF and CDF, respectively, and defining d as
the terms are computed as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The mean and variance of ![]() are thus approximated by
are thus approximated by
and
The approximate power is computed as
|
|
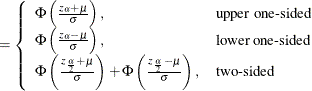 |
The approximate sample size is computed by numerical inversion.
For the normal approximation test with continuity adjustment using the sample variance, the test statistic is
where ![]() .
.
For the METHOD=EXACT option, the computations are the same as described in the section Exact Test of a Binomial Proportion (TEST=EXACT) except for the definitions of the critical values.
For the upper one-sided case,
|
|
|
For the lower one-sided case,
|
|
|
For the two-sided case,
|
|
|
|
|
|
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , where
, where ![]() and
and ![]() are derived as follows.
are derived as follows.
For convenience of notation, define
Then
and
|
|
|
|
|
|
The probabilities ![]() ,
, ![]() , and
, and ![]() and the truncated expectations
and the truncated expectations ![]() and
and ![]() are approximated by assuming the normal-approximate distribution of X,
are approximated by assuming the normal-approximate distribution of X, ![]() . Letting
. Letting ![]() and
and ![]() denote the standard normal PDF and CDF, respectively, and defining d as
denote the standard normal PDF and CDF, respectively, and defining d as
the terms are computed as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The mean and variance of ![]() are thus approximated by
are thus approximated by
and
The approximate power is computed as
|
|
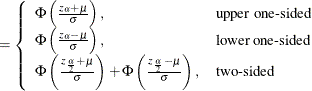 |
The approximate sample size is computed by numerical inversion.
The hypotheses for the equivalence test are
|
|
|
|
|
|
where ![]() and
and ![]() are the lower and upper equivalence bounds, respectively.
are the lower and upper equivalence bounds, respectively.
The analysis is the two one-sided tests (TOST) procedure as described in Chow, Shao, and Wang (2003) on p. 84, but using exact critical values as on p. 116 instead of normal-based critical values.
Two different hypothesis tests are carried out:
|
|
|
|
|
|
and
|
|
|
|
|
|
If ![]() is rejected in favor of
is rejected in favor of ![]() and
and ![]() is rejected in favor of
is rejected in favor of ![]() , then
, then ![]() is rejected in favor of
is rejected in favor of ![]() .
.
The test statistic for each of the two tests (![]() versus
versus ![]() and
and ![]() versus
versus ![]() ) is
) is
Let ![]() denote the critical value of the exact upper one-sided test of
denote the critical value of the exact upper one-sided test of ![]() versus
versus ![]() , and let
, and let ![]() denote the critical value of the exact lower one-sided test of
denote the critical value of the exact lower one-sided test of ![]() versus
versus ![]() . These critical values are computed in the section Exact Test of a Binomial Proportion (TEST=EXACT). Both of these tests are rejected if and only if
. These critical values are computed in the section Exact Test of a Binomial Proportion (TEST=EXACT). Both of these tests are rejected if and only if ![]() . Thus, the exact power of the equivalence test is
. Thus, the exact power of the equivalence test is
|
|
|
|
|
|
The probabilities are computed using Johnson and Kotz (1970, equation 3.20).
The hypotheses for the equivalence test are
|
|
|
|
|
|
where ![]() and
and ![]() are the lower and upper equivalence bounds, respectively.
are the lower and upper equivalence bounds, respectively.
The analysis is the two one-sided tests (TOST) procedure as described in Chow, Shao, and Wang (2003) on p. 84, but using the null variance instead of the sample variance.
Two different hypothesis tests are carried out:
|
|
|
|
|
|
and
|
|
|
|
|
|
If ![]() is rejected in favor of
is rejected in favor of ![]() and
and ![]() is rejected in favor of
is rejected in favor of ![]() , then
, then ![]() is rejected in favor of
is rejected in favor of ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
The test statistic for the test of ![]() versus
versus ![]() is
is
For the METHOD=EXACT option, let ![]() denote the critical value of the exact upper one-sided test of
denote the critical value of the exact upper one-sided test of ![]() versus
versus ![]() using
using ![]() . This critical value is computed in the section z Test for Binomial Proportion Using Null Variance (TEST=Z VAREST=NULL). Similarly, let
. This critical value is computed in the section z Test for Binomial Proportion Using Null Variance (TEST=Z VAREST=NULL). Similarly, let ![]() denote the critical value of the exact lower one-sided test of
denote the critical value of the exact lower one-sided test of ![]() versus
versus ![]() using
using ![]() . Both of these tests are rejected if and only if
. Both of these tests are rejected if and only if ![]() . Thus, the exact power of the equivalence test is
. Thus, the exact power of the equivalence test is
|
|
|
|
|
|
The probabilities are computed using Johnson and Kotz (1970, equation 3.20).
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
and the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
(see Chow, Shao, and Wang (2003, p. 84)). The approximate power is computed as
|
|
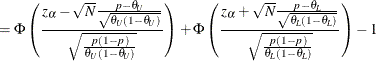 |
The approximate sample size is computed by numerically inverting the power formula, using the sample size estimate ![]() of Chow, Shao, and Wang (2003, p. 85) as an initial guess:
of Chow, Shao, and Wang (2003, p. 85) as an initial guess:
The hypotheses for the equivalence test are
|
|
|
|
|
|
where ![]() and
and ![]() are the lower and upper equivalence bounds, respectively.
are the lower and upper equivalence bounds, respectively.
The analysis is the two one-sided tests (TOST) procedure as described in Chow, Shao, and Wang (2003) on p. 84.
Two different hypothesis tests are carried out:
|
|
|
|
|
|
and
|
|
|
|
|
|
If ![]() is rejected in favor of
is rejected in favor of ![]() and
and ![]() is rejected in favor of
is rejected in favor of ![]() , then
, then ![]() is rejected in favor of
is rejected in favor of ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
where ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
For the METHOD=EXACT option, let ![]() denote the critical value of the exact upper one-sided test of
denote the critical value of the exact upper one-sided test of ![]() versus
versus ![]() using
using ![]() . This critical value is computed in the section z Test for Binomial Proportion Using Sample Variance (TEST=Z VAREST=SAMPLE). Similarly, let
. This critical value is computed in the section z Test for Binomial Proportion Using Sample Variance (TEST=Z VAREST=SAMPLE). Similarly, let ![]() denote the critical value of the exact lower one-sided test of
denote the critical value of the exact lower one-sided test of ![]() versus
versus ![]() using
using ![]() . Both of these tests are rejected if and only if
. Both of these tests are rejected if and only if ![]() . Thus, the exact power of the equivalence test is
. Thus, the exact power of the equivalence test is
|
|
|
|
|
|
The probabilities are computed using Johnson and Kotz (1970, equation 3.20).
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
and the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution
(see Chow, Shao, and Wang (2003), p. 84).
The approximate power is computed as
|
|
|
The approximate sample size is computed by numerically inverting the power formula, using the sample size estimate ![]() of Chow, Shao, and Wang (2003, p. 85) as an initial guess:
of Chow, Shao, and Wang (2003, p. 85) as an initial guess:
The hypotheses for the equivalence test are
|
|
|
|
|
|
where ![]() and
and ![]() are the lower and upper equivalence bounds, respectively.
are the lower and upper equivalence bounds, respectively.
The analysis is the two one-sided tests (TOST) procedure as described in Chow, Shao, and Wang (2003) on p. 84, but using the null variance instead of the sample variance.
Two different hypothesis tests are carried out:
|
|
|
|
|
|
and
|
|
|
|
|
|
If ![]() is rejected in favor of
is rejected in favor of ![]() and
and ![]() is rejected in favor of
is rejected in favor of ![]() , then
, then ![]() is rejected in favor of
is rejected in favor of ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
where ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
For the METHOD=EXACT option, let ![]() denote the critical value of the exact upper one-sided test of
denote the critical value of the exact upper one-sided test of ![]() versus
versus ![]() using
using ![]() . This critical value is computed in the section z Test for Binomial Proportion with Continuity Adjustment Using Null Variance (TEST=ADJZ VAREST=NULL). Similarly, let
. This critical value is computed in the section z Test for Binomial Proportion with Continuity Adjustment Using Null Variance (TEST=ADJZ VAREST=NULL). Similarly, let ![]() denote the critical value of the exact lower one-sided test of
denote the critical value of the exact lower one-sided test of ![]() versus
versus ![]() using
using ![]() . Both of these tests are rejected if and only if
. Both of these tests are rejected if and only if ![]() . Thus, the exact power of the equivalence test is
. Thus, the exact power of the equivalence test is
|
|
|
|
|
|
The probabilities are computed using Johnson and Kotz (1970, equation 3.20).
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , and
, and ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , where
, where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are derived as follows.
are derived as follows.
For convenience of notation, define
|
|
|
|
|
|
Then
|
|
|
|
|
|
and
|
|
|
|
|
|
|
|
|
|
|
|
The probabilities ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and the truncated expectations
and the truncated expectations ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are approximated by assuming the normal-approximate distribution of X,
are approximated by assuming the normal-approximate distribution of X, ![]() . Letting
. Letting ![]() and
and ![]() denote the standard normal PDF and CDF, respectively, and defining
denote the standard normal PDF and CDF, respectively, and defining ![]() and
and ![]() as
as
|
|
|
|
the terms are computed as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The mean and variance of ![]() and
and ![]() are thus approximated by
are thus approximated by
|
|
|
|
|
|
and
|
|
|
|
|
|
The approximate power is computed as
|
|
|
The approximate sample size is computed by numerically inverting the power formula.
The hypotheses for the equivalence test are
|
|
|
|
|
|
where ![]() and
and ![]() are the lower and upper equivalence bounds, respectively.
are the lower and upper equivalence bounds, respectively.
The analysis is the two one-sided tests (TOST) procedure as described in Chow, Shao, and Wang (2003) on p. 84.
Two different hypothesis tests are carried out:
|
|
|
|
|
|
and
|
|
|
|
|
|
If ![]() is rejected in favor of
is rejected in favor of ![]() and
and ![]() is rejected in favor of
is rejected in favor of ![]() , then
, then ![]() is rejected in favor of
is rejected in favor of ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
where ![]() .
.
The test statistic for the test of ![]() versus
versus ![]() is
is
For the METHOD=EXACT option, let ![]() denote the critical value of the exact upper one-sided test of
denote the critical value of the exact upper one-sided test of ![]() versus
versus ![]() using
using ![]() . This critical value is computed in the section z Test for Binomial Proportion with Continuity Adjustment Using Sample Variance (TEST=ADJZ VAREST=SAMPLE). Similarly, let
. This critical value is computed in the section z Test for Binomial Proportion with Continuity Adjustment Using Sample Variance (TEST=ADJZ VAREST=SAMPLE). Similarly, let ![]() denote the critical value of the exact lower one-sided test of
denote the critical value of the exact lower one-sided test of ![]() versus
versus ![]() using
using ![]() . Both of these tests are rejected if and only if
. Both of these tests are rejected if and only if ![]() . Thus, the exact power of the equivalence test is
. Thus, the exact power of the equivalence test is
|
|
|
|
|
|
The probabilities are computed using Johnson and Kotz (1970, equation 3.20).
For the METHOD=NORMAL option, the test statistic ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , and
, and ![]() is assumed to have the normal distribution
is assumed to have the normal distribution ![]() , where
, where ![]() ,
, ![]() ,
, ![]() and
and ![]() are derived as follows.
are derived as follows.
For convenience of notation, define
Then
|
|
|
|
|
|
and
|
|
|
|
|
|
|
|
|
|
|
|
The probabilities ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and the truncated expectations
and the truncated expectations ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are approximated by assuming the normal-approximate distribution of X,
are approximated by assuming the normal-approximate distribution of X, ![]() . Letting
. Letting ![]() and
and ![]() denote the standard normal PDF and CDF, respectively, and defining
denote the standard normal PDF and CDF, respectively, and defining ![]() and
and ![]() as
as
|
|
|
|
the terms are computed as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The mean and variance of ![]() and
and ![]() are thus approximated by
are thus approximated by
|
|
|
|
|
|
and
|
|
|
|
|
|
The approximate power is computed as
|
|
|
The approximate sample size is computed by numerically inverting the power formula.
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
![\[ \frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \quad \pm \quad \frac{z_{1-\alpha /2} N^\frac {1}{2}}{N + z^2_{1-\alpha /2}} \left(\hat{p}(1-\hat{p}) + \frac{z^2_{1-\alpha /2}}{4N} \right)^\frac {1}{2} \]](images/statug_power0493.png)
So the half-width for the two-sided ![]() % confidence interval is
% confidence interval is
![\[ \mbox{half-width} = \frac{z_{1-\alpha /2} N^\frac {1}{2}}{N + z^2_{1-\alpha /2}} \left(\hat{p}(1-\hat{p}) + \frac{z^2_{1-\alpha /2}}{4N} \right)^\frac {1}{2} \]](images/statug_power0494.png)
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h:
For references and more details about this and all other confidence intervals associated with the CI= option, see Binomial Proportion of Chapter 38: The FREQ Procedure.
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
![\[ \frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \quad \pm \quad z_{1-\alpha /2} \left( \frac{\frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \left(1 -\frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \right)}{N + z^2_{1-\alpha /2}} \right)^\frac {1}{2} \]](images/statug_power0497.png)
So the half-width for the two-sided ![]() % confidence interval is
% confidence interval is
![\[ \mbox{half-width} = z_{1-\alpha /2} \left( \frac{\frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \left(1 -\frac{X + \frac{z^2_{1-\alpha /2}}{2}}{N + z^2_{1-\alpha /2}} \right)}{N + z^2_{1-\alpha /2}} \right)^\frac {1}{2} \]](images/statug_power0498.png)
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h:
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
where
and
The half-width of this two-sided ![]() % confidence interval is defined as half the width of the full interval:
% confidence interval is defined as half the width of the full interval:
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h:
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
where
and
The half-width of this two-sided ![]() % confidence interval is defined as half the width of the full interval:
% confidence interval is defined as half the width of the full interval:
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h:
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
So the half-width for the two-sided ![]() % confidence interval is
% confidence interval is
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h:
The two-sided ![]() % confidence interval for p is
% confidence interval for p is
So the half-width for the two-sided ![]() % confidence interval is
% confidence interval is
Prob(Width) is calculated exactly by adding up the probabilities of observing each ![]() that produces a confidence interval whose half-width is at most a target value h:
that produces a confidence interval whose half-width is at most a target value h: