The SEQTEST Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics
Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary
Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary - References
Example 84.8 Testing an Effect in a Logistic Regression Model
This example requests a two-sided test for the dose effect in a dose-response model (Whitehead, 1997, pp. 262–263). Consider the logistic regression model
|
|
where ![]() is the response probability to be modeled for the binary response
is the response probability to be modeled for the binary response Resp and LDose = log( Dose +1) is the covariate. The dose levels are 0 for the control group, and they are 1, 3, and 6 for the three treatment groups.
Following the derivations in the section “Test for a Parameter in the Logistic Regression Model” in the chapter “The SEQDESIGN Procedure,” the required sample size can be derived from
|
|
where ![]() is the variance of the response variable in the logistic regression model,
is the variance of the response variable in the logistic regression model, ![]() is the proportion of variance of
is the proportion of variance of LDose explained by other covariates, and ![]() is the variance of
is the variance of LDose.
Since LDose is the only covariate in the model, ![]() . For a logistic model, the variance
. For a logistic model, the variance ![]() can be estimated by
can be estimated by
|
|
where ![]() is the estimated probability of the response variable
is the estimated probability of the response variable Resp. Thus, the sample size can be computed as
|
|
The null hypothesis ![]() corresponds to no treatment effect. Suppose that the alternative hypothesis
corresponds to no treatment effect. Suppose that the alternative hypothesis ![]() is the reference improvement that should be detected at a 0.90 level.
is the reference improvement that should be detected at a 0.90 level.
Note that ![]() corresponds to an odds ratio of 2 between the treatment group with dose level 3 and the control group. The log odds ratio
between the two groups is
corresponds to an odds ratio of 2 between the treatment group with dose level 3 and the control group. The log odds ratio
between the two groups is
|
|
which corresponds to
|
|
If the same number of patients are assigned in each of the four groups, then the MLE of the variance of LDose is ![]() . Further, if the response rate is 0.40, then the required sample size can be derived using the SAMPLESIZE statement in the
SEQDESIGN procedure.
. Further, if the response rate is 0.40, then the required sample size can be derived using the SAMPLESIZE statement in the
SEQDESIGN procedure.
The following statements invoke the SEQDESIGN procedure and request a three-stage group sequential design for normally distributed
data. The design has a null hypothesis of no treatment effect ![]() with early stopping to reject the null hypothesis with a two-sided alternative hypothesis
with early stopping to reject the null hypothesis with a two-sided alternative hypothesis ![]() .
.
ods graphics on;
proc seqdesign altref=0.5;
TwoSidedErrorSpending: design method=errfuncpow
method(loweralpha)=errfuncpow(rho=1)
method(upperalpha)=errfuncpow(rho=3)
nstages=3
stop=both;
samplesize model=logistic( prop=0.4 xvariance=0.5345);
ods output Boundary=Bnd_Dose;
run;
ods graphics off;
The ODS OUTPUT statement with the BOUNDARY=BND_DOSE option creates an output data set named BND_DOSE which contains the resulting boundary information for the subsequent sequential tests.
The “Design Information” table in Output 84.8.1 displays design specifications and derived statistics. Since the alternative reference is specified, the maximum information 47.22445 is derived.
Output 84.8.1: Error Spending Design Information
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Two-Sided |
| Early Stop | Accept/Reject Null |
| Method | Error Spending |
| Boundary Key | Both |
| Alternative Reference | 0.5 |
| Number of Stages | 3 |
| Alpha | 0.05 |
| Beta (Lower) | 0.1 |
| Beta (Upper) | 0.07871 |
| Power (Lower) | 0.9 |
| Power (Upper) | 0.92129 |
| Max Information (Percent of Fixed Sample) | 103.7223 |
| Max Information | 47.22445 |
| Null Ref ASN (Percent of Fixed Sample) | 79.47628 |
| Lower Alt Ref ASN (Sample Size) | 234.1646 |
| Upper Alt Ref ASN (Sample Size) | 270.4058 |
The “Boundary Information” table in Output 84.8.2 displays the information level, alternative reference, and boundary values at each stage. By default (or equivalently if you specify BOUNDARYSCALE=STDZ), the boundary values are displayed with the standardized Z statistic scale.
Output 84.8.2: Boundary Information
| Boundary Information (Standardized Z Scale) Null Reference = 0 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||||||
| Information Level | Reference | Lower | Upper | ||||||
| Proportion | Actual | N | Lower | Upper | Alpha | Beta | Beta | Alpha | |
| 1 | 0.3333 | 15.74148 | 122.7119 | -1.98378 | 1.98378 | -2.39398 | . | . | 3.11302 |
| 2 | 0.6667 | 31.48297 | 245.4238 | -2.80548 | 2.80548 | -2.29380 | -1.02812 | 0.91855 | 2.46193 |
| 3 | 1.0000 | 47.22445 | 368.1357 | -3.43600 | 3.43600 | -2.17479 | -2.17479 | 1.98311 | 1.98311 |
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 84.8.3.
Output 84.8.3: Boundary Plot
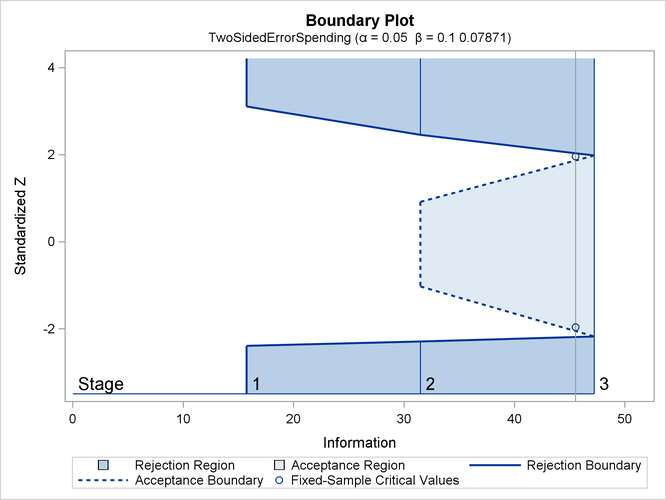
With the SAMPLESIZE statement, the “Sample Size Summary” table in Output 84.8.4 displays the parameters for the sample size computation.
Output 84.8.4: Required Sample Size Summary
| Sample Size Summary | |
|---|---|
| Test | Logistic Reg Parameter |
| Parameter | 0.5 |
| Proportion | 0.4 |
| X Variance | 0.5345 |
| R Square (X) | 0 |
| Max Sample Size | 368.1357 |
| Expected Sample Size (Null Ref) | 282.0807 |
| Expected Sample Size (Alt Ref) | 270.4058 |
The “Sample Sizes” table in Output 84.8.5 displays the required sample sizes for the group sequential clinical trial.
Output 84.8.5: Required Sample Sizes
| Sample Sizes (N) Z Test for Logistic Regression Parameter |
||||
|---|---|---|---|---|
| _Stage_ | Fractional N | Ceiling N | ||
| N | Information | N | Information | |
| 1 | 122.71 | 15.7415 | 123 | 15.7784 |
| 2 | 245.42 | 31.4830 | 246 | 31.5569 |
| 3 | 368.14 | 47.2245 | 369 | 47.3353 |
That is, 123 new patients are needed in each stage and the number is rounded up to 124 for each stage to have a multiple of four for the four dose levels in the trial. Note that since the sample sizes are derived from an estimated response probability and are rounded up, the actual information levels might not match the corresponding target information levels.
Output 84.8.6 lists the first 10 observations of the trial data.
Output 84.8.6: Clinical Trial Data
| First 10 Obs in the Trial Data |
| Obs | Resp | Dose | LDose |
|---|---|---|---|
| 1 | 0 | 0 | 0.00000 |
| 2 | 0 | 1 | 0.69315 |
| 3 | 1 | 3 | 1.38629 |
| 4 | 1 | 6 | 1.94591 |
| 5 | 1 | 0 | 0.00000 |
| 6 | 1 | 1 | 0.69315 |
| 7 | 1 | 3 | 1.38629 |
| 8 | 1 | 6 | 1.94591 |
| 9 | 0 | 0 | 0.00000 |
| 10 | 0 | 1 | 0.69315 |
The following statements use the LOGISTIC procedure to estimate the slope ![]() and its associated standard error at stage 1:
and its associated standard error at stage 1:
proc logistic data=Dose_1; model Resp(event='1')= LDose; ods output ParameterEstimates=Parms_Dose1; run;
The following statements create and display (in Output 84.8.7) the input data set that contains slope ![]() and its associated standard error for the SEQTEST procedure:
and its associated standard error for the SEQTEST procedure:
data Parms_Dose1; set Parms_Dose1; if Variable='LDose'; _Scale_='MLE'; _Stage_= 1; keep _Scale_ _Stage_ Variable Estimate StdErr; run; proc print data=Parms_Dose1; title 'Statistics Computed at Stage 1'; run;
Output 84.8.7: Statistics Computed at Stage 1
| Statistics Computed at Stage 1 |
| Obs | Variable | Estimate | StdErr | _Scale_ | _Stage_ |
|---|---|---|---|---|---|
| 1 | LDose | 0.5741 | 0.2544 | MLE | 1 |
The following statements invoke the SEQTEST procedure to test for early stopping at stage 1:
ods graphics on;
proc seqtest Boundary=Bnd_Dose
Parms(testvar=LDose)=Parms_Dose1
infoadj=prop
order=mle
boundaryscale=mle
;
ods output Test=Test_Dose1;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage 1, which was
generated in the SEQDESIGN procedure. The PARMS=PARMS_DOSE1 option specifies the input data set PARMS_DOSE1 that contains the test statistic and its associated standard error at stage 1, and the TESTVAR=LDOSE option identifies the
test variable LDOSE in the data set.
If the computed information level for stage 1 is not the same as the value provided in the BOUNDARY= data set, the INFOADJ=PROP option (which is the default) proportionally adjusts the information levels at future interim stages from the levels provided in the BOUNDARY= data set. The ORDER=MLE option uses the MLE ordering to derive the p-value, the unbiased median estimate, and the confidence limits for the regression slope estimate.
The ODS OUTPUT statement with the TEST=TEST_DOSE1 option creates an output data set named TEST_DOSE1 which contains the updated boundary information for the test at stage 1. The data set also provides the boundary information
that is needed for the group sequential test at the next stage.
The “Design Information” table in Output 84.8.8 displays design specifications. By default (or equivalently if you specify BOUNDARYKEY=ALPHA), the boundary values are modified
for the new information levels to maintain the Type I ![]() level. The maximum information remains the same as the design stored in the BOUNDARY= data set, but the derived Type II error
probability
level. The maximum information remains the same as the design stored in the BOUNDARY= data set, but the derived Type II error
probability ![]() and power
and power ![]() are different because of the new information levels.
are different because of the new information levels.
Output 84.8.8: Design Information
| Design Information | |
|---|---|
| BOUNDARY Data Set | WORK.BND_DOSE |
| Data Set | WORK.PARMS_DOSE1 |
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Two-Sided |
| Early Stop | Accept/Reject Null |
| Number of Stages | 3 |
| Alpha | 0.05 |
| Beta (Lower) | 0.09992 |
| Beta (Upper) | 0.07871 |
| Power (Lower) | 0.90008 |
| Power (Upper) | 0.92129 |
| Max Information (Percent of Fixed Sample) | 103.7231 |
| Max Information | 47.2244524 |
| Null Ref ASN (Percent of Fixed Sample) | 79.45049 |
| Lower Alt Ref ASN (Percent of Fixed Sample) | 66.05269 |
| Upper Alt Ref ASN (Percent of Fixed Sample) | 76.24189 |
The “Test Information” table in Output 84.8.9 displays the boundary values for the test statistic with the specified MLE scale.
Output 84.8.9: Sequential Tests
| Test Information (MLE Scale) Null Reference = 0 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | |||||||
| Information Level | Reference | Lower | Upper | LDose | ||||||
| Proportion | Actual | Lower | Upper | Alpha | Beta | Beta | Alpha | Estimate | Action | |
| 1 | 0.3272 | 15.45062 | -0.50000 | 0.50000 | -0.61078 | . | . | 0.79337 | 0.57409 | Continue |
| 2 | 0.6636 | 31.33753 | -0.50000 | 0.50000 | -0.40974 | -0.18169 | 0.16222 | 0.44033 | . | |
| 3 | 1.0000 | 47.22445 | -0.50000 | 0.50000 | -0.31633 | -0.31633 | 0.28860 | 0.28860 | . | |
The information level at stage 1 is derived from the standard error ![]() in the PARMS= data set,
in the PARMS= data set,
|
|
With the INFOADJ=PROP option (which is the default), the information level at stage 2 is derived proportionally from the observed
information at stage 1 and the information levels in the BOUNDARY= data set. At stage 1, the ![]() boundary values are missing and there is no early stopping to accept
boundary values are missing and there is no early stopping to accept ![]() . The MLE statistic 0.57409 is between the lower and upper
. The MLE statistic 0.57409 is between the lower and upper ![]() boundaries, so the trial continues to the next stage.
boundaries, so the trial continues to the next stage.
With ODS Graphics enabled, a boundary plot with the boundary values and test statistics is displayed, as shown in Output 84.8.10. As expected, the test statistic is in the continuation region below the upper alpha boundary.
Output 84.8.10: Sequential Test Plot
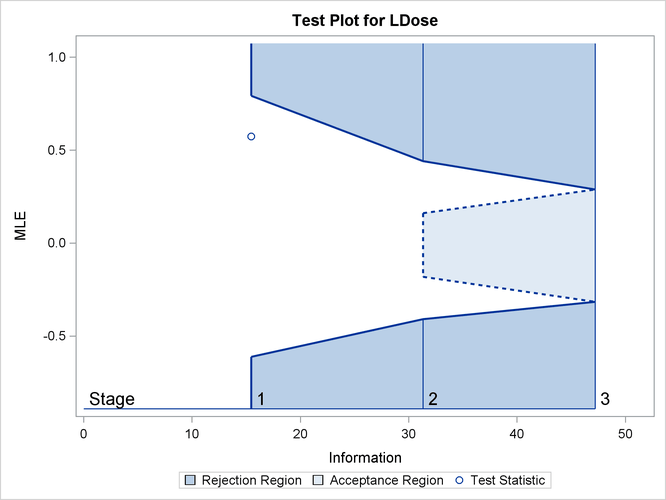
The following statements use the LOGISTIC procedure to estimate the slope ![]() and its associated standard error at stage 2:
and its associated standard error at stage 2:
proc logistic data=dose_2; model Resp(event='1')=LDose; ods output ParameterEstimates=Parms_Dose2; run;
The following statements create and display (in Output 84.8.11) the input data set that contains slope ![]() and its associated standard error at stage 2 for the SEQTEST procedure:
and its associated standard error at stage 2 for the SEQTEST procedure:
data Parms_Dose2; set Parms_Dose2; if Variable='LDose'; _Scale_='MLE'; _Stage_= 2; keep _Scale_ _Stage_ Variable Estimate StdErr; run; proc print data=Parms_Dose2; title 'Statistics Computed at Stage 2'; run;
Output 84.8.11: Statistics Computed at Stage 2
| Statistics Computed at Stage 2 |
| Obs | Variable | Estimate | StdErr | _Scale_ | _Stage_ |
|---|---|---|---|---|---|
| 1 | LDose | 0.5213 | 0.1788 | MLE | 2 |
The following statements invoke the SEQTEST procedure to test for early stopping at stage 2:
ods graphics on;
proc seqtest Boundary=Test_Dose1
Parms(Testvar=LDose)=Parms_Dose2
infoadj=prop
order=mle
boundaryscale=mle
rci
plots=rci
;
ods output Test=Test_Dose2;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage 2, which was generated by the SEQTEST procedure at the previous stage. The PARMS= option specifies the input data set that contains the test statistic and its associated standard error at stage 2, and the TESTVAR= option identifies the test variable in the data set.
The ORDER=MLE option uses the MLE ordering to derive the p-value, unbiased median estimate, and confidence limits for the regression slope estimate.
The ODS OUTPUT statement with the TEST=TEST_DOSE2 option creates an output data set named TEST_DOSE2 which contains the updated boundary information for the test at stage 2. The data set also provides the boundary information
that is needed for the group sequential test at the next stage.
The “Design Information” table in Output 84.8.12 displays design specifications. By default (or equivalently if you specify BOUNDARYKEY=ALPHA), the boundary values are modified
for the new information levels to maintain the Type I ![]() level.
level.
Output 84.8.12: Design Information
| Design Information | |
|---|---|
| BOUNDARY Data Set | WORK.TEST_DOSE1 |
| Data Set | WORK.PARMS_DOSE2 |
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Two-Sided |
| Early Stop | Accept/Reject Null |
| Number of Stages | 3 |
| Alpha | 0.05 |
| Beta (Lower) | 0.0999 |
| Beta (Upper) | 0.07871 |
| Power (Lower) | 0.9001 |
| Power (Upper) | 0.92129 |
| Max Information (Percent of Fixed Sample) | 103.7227 |
| Max Information | 47.2244524 |
| Null Ref ASN (Percent of Fixed Sample) | 79.44086 |
| Lower Alt Ref ASN (Percent of Fixed Sample) | 66.04641 |
| Upper Alt Ref ASN (Percent of Fixed Sample) | 76.22739 |
The information is derived from the standard error associated with the slope estimate at the final stage and is larger than
the target level. The derived Type II error probability ![]() and power
and power ![]() are different because of the new information levels.
are different because of the new information levels.
The “Test Information” table in Output 84.8.13 displays the boundary values for the test statistic with the specified MLE scale. The information levels are derived from
the standard errors in the PARMS= data set. At stage 2, the slope estimate 0.52128 is larger than 0.44091, the upper ![]() boundary value, the trial stops to reject the null hypothesis of no treatment effect.
boundary value, the trial stops to reject the null hypothesis of no treatment effect.
Output 84.8.13: Sequential Tests
| Test Information (MLE Scale) Null Reference = 0 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | |||||||
| Information Level | Reference | Lower | Upper | LDose | ||||||
| Proportion | Actual | Lower | Upper | Alpha | Beta | Beta | Alpha | Estimate | Action | |
| 1 | 0.3272 | 15.45062 | -0.50000 | 0.50000 | -0.61078 | . | . | 0.79337 | 0.57409 | Continue |
| 2 | 0.6624 | 31.28346 | -0.50000 | 0.50000 | -0.41028 | -0.18112 | 0.16166 | 0.44091 | 0.52128 | Reject Null |
| 3 | 1.0000 | 47.22445 | -0.50000 | 0.50000 | -0.31628 | -0.31628 | 0.28861 | 0.28861 | . | |
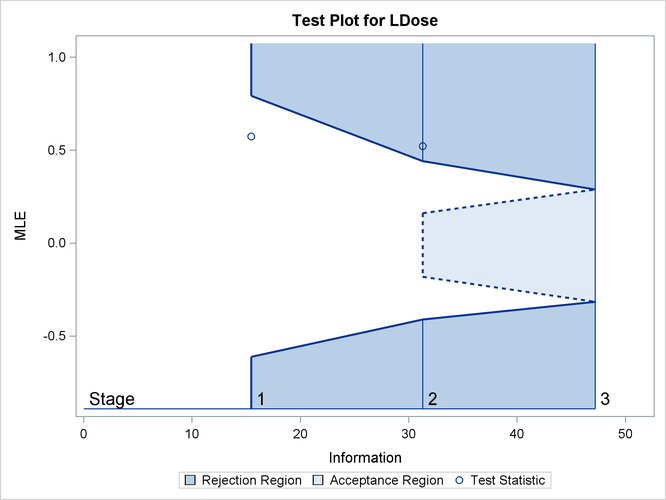
With ODS Graphics enabled, a boundary plot with the boundary values and test statistics is displayed, as shown in Output 84.8.14. As expected, the test statistic is above the upper ![]() boundary in the upper rejection region at stage 2.
boundary in the upper rejection region at stage 2.
Output 84.8.14: Sequential Test Plot
After a trial is stopped, the “Parameter Estimates” table in Output 84.8.15 displays the stopping stage, parameter estimate, unbiased median estimate, confidence limits, and the p-value under the null hypothesis ![]() .
.
Output 84.8.15: Parameter Estimates
| Parameter Estimates MLE Ordering |
||||||
|---|---|---|---|---|---|---|
| Parameter | Stopping Stage |
MLE | p-Value for H0:Parm=0 |
Median Estimate |
95% Confidence Limits | |
| LDose | 2 | 0.521275 | 0.0050 | 0.502647 | 0.15745 | 0.85154 |
With the ORDER=MLE option, the MLE ordering is used to compute the p-value, unbiased median estimate, and confidence limits. As expected, the p-value 0.005 is significant at the ![]() level and the confidence interval does not contain the null reference zero.
level and the confidence interval does not contain the null reference zero.
With the RCI option, the “Repeated Confidence Intervals” table in Output 84.8.16 displays repeated confidence intervals for the parameter. For a two-sided test, since the rejection lower repeated confidence limit 0.0804 is greater than the null reference zero, the trial is stopped to reject the hypothesis.
Output 84.8.16: Repeated Confidence Intervals
| Repeated Confidence Intervals | ||||||
|---|---|---|---|---|---|---|
| _Stage_ | Information Level |
Parameter Estimate |
Rejection Boundary | Acceptance Boundary | ||
| Lower 97.5% Repeated CL | Upper 97.5% Repeated CL | Lower 90.01% Repeated CL | Upper 92.13% Repeated CL | |||
| 1 | 15.4506 | 0.57409 | -0.2193 | 1.1849 | . | . |
| 2 | 31.2835 | 0.52128 | 0.0804 | 0.9316 | 0.2024 | 0.8596 |
With the PLOTS=RCI option, the “Repeated Confidence Intervals Plot” displays repeated confidence intervals for the parameter, as shown in Output 84.8.17. It shows that the null reference zero is inside the rejection repeated confidence interval at stage 1 but outside the rejection repeated confidence interval at stage 2. This implies that the study stops at stage 2 to reject the hypothesis.
Output 84.8.17: Repeated Confidence Intervals Plot
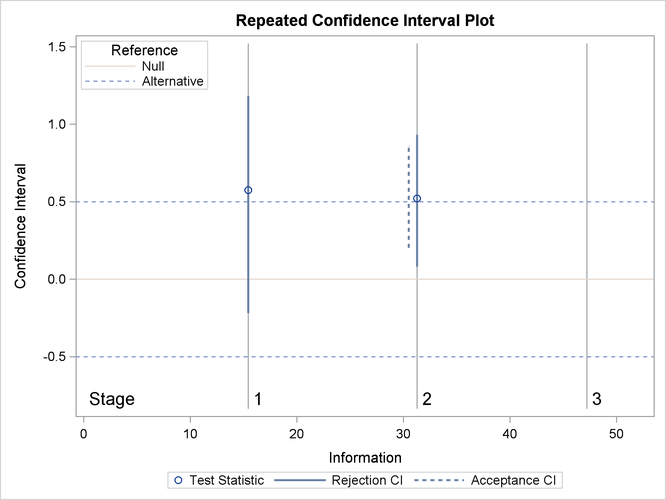
Note that the hypothesis is accepted if at any stage, the acceptance repeated confidence interval falls within the interval
![]() of the alternative references.
of the alternative references.