The SEQTEST Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics
Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary
Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary - References
Applicable Tests and Sample Size Computation
The SEQDESIGN procedure assumes that the data are from a multivariate normal distribution and the sequence of the standardized
test statistics ![]() have the following canonical joint distribution:
have the following canonical joint distribution:
-
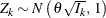
-
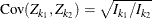 ,
, 
where K is the total number of stages and ![]() is the information available at stage k.
is the information available at stage k.
If the data are not from a normal distribution such as binomial distribution, then it is assumed that the test statistic is computed from a large sample such that the statistic has an approximately normal distribution.
In a clinical trial, the sample size required depends on the Type I error probability ![]() , reference improvement
, reference improvement ![]() , power
, power ![]() , and variance of the response variable. Given a null hypothesis
, and variance of the response variable. Given a null hypothesis ![]() with an upper alternative hypothesis
with an upper alternative hypothesis ![]() , the information required for a fixed-sample test is given by
, the information required for a fixed-sample test is given by
|
|
where the parameter ![]() depends on the test specified in the clinical trial. For example, if you are comparing two binomial populations
depends on the test specified in the clinical trial. For example, if you are comparing two binomial populations ![]() , then
, then ![]() is the difference between two proportions if the proportion difference statistic is used, and
is the difference between two proportions if the proportion difference statistic is used, and ![]() , the log odds ratio for the two proportions if the log odds ratio statistic is used.
, the log odds ratio for the two proportions if the log odds ratio statistic is used.
If the maximum likelihood estimate ![]() from the likelihood function can be derived, then the asymptotic variance for
from the likelihood function can be derived, then the asymptotic variance for ![]() is Var
is Var![]() , where I is Fisher’s information for
, where I is Fisher’s information for ![]() .
.
The resulting statistic ![]() corresponds to the MLE scale as specified in the BOUNDARYSCALE=MLE option in the PROC SEQDESIGN statement,
corresponds to the MLE scale as specified in the BOUNDARYSCALE=MLE option in the PROC SEQDESIGN statement, ![]() corresponds to the standardized Z scale (BOUNDARYSCALE=STDZ), and
corresponds to the standardized Z scale (BOUNDARYSCALE=STDZ), and ![]() corresponds to the score scale (BOUNDARYSCALE=SCORE).
corresponds to the score scale (BOUNDARYSCALE=SCORE).
Alternatively, if the score statistic is derived, it can also be used as the test statistic and its asymptotic variance is given by Fisher’s information.
For a group sequential trial, the maximum information ![]() is derived in the SEQDESIGN procedure by using the specified
is derived in the SEQDESIGN procedure by using the specified ![]() ,
, ![]() , and
, and ![]() . With the maximum information
. With the maximum information
|
|
the sample size required for a specified test statistic in the trial can be evaluated or estimated from the known or estimated variance of the response variable. Note that different designs might produce different maximum information levels for the same hypothesis, and this in turn might require a different number of observations for the trial.
With a specified test statistic, the required sample sizes at the stages can be computed. These tests include commonly used tests for normal means, binomial proportions, and survival distributions. See the section “Sample Size Computation” in “The SEQDESIGN Procedure” for a description of these tests.