The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Regression Diagnostics
For binary response data, regression diagnostics developed by Pregibon (1981) can be requested by specifying the INFLUENCE option. For diagnostics available with conditional logistic regression, see the section Regression Diagnostic Details. These diagnostics can also be obtained from the OUTPUT statement.
This section uses the following notation:
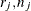
-
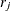 is the number of event responses out of
is the number of event responses out of 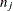 trials for the jth observation. If events/trials syntax is used,
trials for the jth observation. If events/trials syntax is used, 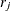 is the value of events and
is the value of events and 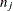 is the value of trials. For single-trial syntax,
is the value of trials. For single-trial syntax, 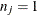 , and
, and 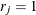 if the ordered response is 1, and
if the ordered response is 1, and 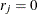 if the ordered response is 2.
if the ordered response is 2.
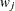
-
is the weight of the jth observation.
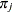
-
is the probability of an event response for the jth observation given by
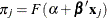 , where
, where 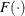 is the inverse link function.
is the inverse link function.
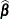
-
is the maximum likelihood estimate (MLE) of
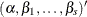 .
.
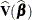
-
is the estimated covariance matrix of
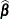 .
.
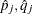
-
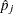 is the estimate of
is the estimate of 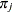 evaluated at
evaluated at 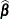 , and
, and 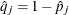 .
.
Pregibon (1981) suggests using the index plots of several diagnostic statistics to identify influential observations and to quantify the effects on various aspects of the maximum likelihood fit. In an index plot, the diagnostic statistic is plotted against the observation number. In general, the distributions of these diagnostic statistics are not known, so cutoff values cannot be given for determining when the values are large. However, the IPLOTS and INFLUENCE options in the MODEL statement and the PLOTS option in the PROC LOGISTIC statement provide displays of the diagnostic values, allowing visual inspection and comparison of the values across observations. In these plots, if the model is correctly specified and fits all observations well, then no extreme points should appear.
The next five sections give formulas for these diagnostic statistics.
Hat Matrix Diagonal (Leverage)
The diagonal elements of the hat matrix are useful in detecting extreme points in the design space where they tend to have larger values. The jth diagonal element is
|
|
where
|
|
|
|
|
|
|
|
and ![]() and
and ![]() are the first and second derivatives of the link function
are the first and second derivatives of the link function ![]() , respectively.
, respectively.
For a binary response logit model, the hat matrix diagonal elements are
|
|
If the estimated probability is extreme (less than 0.1 and greater than 0.9, approximately), then the hat diagonal might be greatly reduced in value. Consequently, when an observation has a very large or very small estimated probability, its hat diagonal value is not a good indicator of the observation’s distance from the design space (Hosmer and Lemeshow, 2000, p. 171).
Residuals
Residuals are useful in identifying observations that are not explained well by the model. Pearson residuals are components of the Pearson chi-square statistic and deviance residuals are components of the deviance. The Pearson residual for the jth observation is
|
|
The Pearson chi-square statistic is the sum of squares of the Pearson residuals.
The deviance residual for the jth observation is
|
|
![$\displaystyle \left\{ \begin{array}{ll} -\sqrt {-2w_ jn_ j\log (\hat{q}_ j)} & \mbox{if }r_ j=0 \\ \pm \sqrt {2w_ j[r_ j\log (\frac{r_ j}{n_ j\hat{p_ j}})+ (n_ j-r_ j)\log (\frac{n_ j-r_ j}{n_ j\hat{q}_ j}) ]} & \mbox{if }0<r_ j<n_ j \\ \sqrt {-2w_ jn_ j\log (\hat{p}_ j)} & \mbox{if }r_ j=n_ j \end{array} \right. $](images/statug_logistic0566.png) |
where the plus (minus) in ![]() is used if
is used if ![]() is greater (less) than
is greater (less) than ![]() . The deviance is the sum of squares of the deviance residuals.
. The deviance is the sum of squares of the deviance residuals.
The STDRES option in the INFLUENCE and PLOTS=INFLUENCE options computes three more residuals (Collett, 2003). The Pearson and deviance residuals are standardized to have approximately unit variance:
|
|
|
|
|
|
|
|
The likelihood residuals, which estimate components of a likelihood ratio test of deleting an individual observation, are a weighted combination of the standardized Pearson and deviance residuals
|
|
|
|
DFBETAS
For each parameter estimate, the procedure calculates a DFBETAS diagnostic for each observation. The DFBETAS diagnostic for an observation is the standardized difference in the parameter estimate due to deleting the observation, and it can be used to assess the effect of an individual observation on each estimated parameter of the fitted model. Instead of reestimating the parameter every time an observation is deleted, PROC LOGISTIC uses the one-step estimate. See the section Predicted Probability of an Event for Classification. For the jth observation, the DFBETAS are given by
|
|
where ![]() is the standard error of the ith component of
is the standard error of the ith component of ![]() , and
, and ![]() is the ith component of the one-step difference
is the ith component of the one-step difference
|
|
![]() is the approximate change (
is the approximate change (![]() ) in the vector of parameter estimates due to the omission of the jth observation. The DFBETAS are useful in detecting observations that are causing instability in the selected coefficients.
) in the vector of parameter estimates due to the omission of the jth observation. The DFBETAS are useful in detecting observations that are causing instability in the selected coefficients.
C and CBAR
C and CBAR are confidence interval displacement diagnostics that provide scalar measures of the influence of individual observations
on ![]() . These diagnostics are based on the same idea as the Cook distance in linear regression theory (Cook and Weisberg, 1982), but use the one-step estimate. C and CBAR for the jth observation are computed as
. These diagnostics are based on the same idea as the Cook distance in linear regression theory (Cook and Weisberg, 1982), but use the one-step estimate. C and CBAR for the jth observation are computed as
|
|
and
|
|
respectively.
Typically, to use these statistics, you plot them against an index and look for outliers.
DIFDEV and DIFCHISQ
DIFDEV and DIFCHISQ are diagnostics for detecting ill-fitted observations; in other words, observations that contribute heavily to the disagreement between the data and the predicted values of the fitted model. DIFDEV is the change in the deviance due to deleting an individual observation while DIFCHISQ is the change in the Pearson chi-square statistic for the same deletion. By using the one-step estimate, DIFDEV and DIFCHISQ for the jth observation are computed as
|
|
and
|
|