The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Receiver Operating Characteristic Curves
ROC curves are used to evaluate and compare the performance of diagnostic tests; they can also be used to evaluate model fit. An ROC curve is just a plot of the proportion of true positives (events predicted to be events) versus the proportion of false positives (nonevents predicted to be events).
In a sample of n individuals, suppose ![]() individuals are observed to have a certain condition or event. Let this group be denoted by
individuals are observed to have a certain condition or event. Let this group be denoted by ![]() , and let the group of the remaining
, and let the group of the remaining ![]() individuals who do not have the condition be denoted by
individuals who do not have the condition be denoted by ![]() . Risk factors are identified for the sample, and a logistic regression model is fitted to the data. For the jth individual, an estimated probability
. Risk factors are identified for the sample, and a logistic regression model is fitted to the data. For the jth individual, an estimated probability ![]() of the event of interest is calculated. Note that the
of the event of interest is calculated. Note that the ![]() are computed as shown in the section Linear Predictor, Predicted Probability, and Confidence Limits and are not the cross validated estimates discussed in the section Classification Table.
are computed as shown in the section Linear Predictor, Predicted Probability, and Confidence Limits and are not the cross validated estimates discussed in the section Classification Table.
Suppose the n individuals undergo a test for predicting the event and the test is based on the estimated probability of the event. Higher values of this estimated probability are assumed to be associated with the event. A receiver operating characteristic (ROC) curve can be constructed by varying the cutpoint that determines which estimated event probabilities are considered to predict the event. For each cutpoint z, the following measures can be output to a data set by specifying the OUTROC= option in the MODEL statement or the OUTROC= option in the SCORE statement:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where ![]() is the indicator function.
is the indicator function.
Note that _POS_(z) is the number of correctly predicted event responses, _NEG_(z) is the number of correctly predicted nonevent responses, _FALPOS_(z) is the number of falsely predicted event responses, _FALNEG_(z) is the number of falsely predicted nonevent responses, _SENSIT_(z) is the sensitivity of the test, and _1MSPEC_(z) is one minus the specificity of the test.
The ROC curve is a plot of sensitivity (_SENSIT_) against 1–specificity (_1MSPEC_). The plot can be produced by using the PLOTS option or by using the GPLOT or SGPLOT procedure with the OUTROC= data set. See Example 54.7 for an illustration. The area under the ROC curve, as determined by the trapezoidal rule, is estimated by the concordance index, c, in the “Association of Predicted Probabilities and Observed Responses” table.
Comparing ROC Curves
ROC curves can be created from each model fit in a selection routine, from the specified model in the MODEL statement, from specified models in ROC statements, or from input variables which act as ![]() in the preceding discussion. Association statistics are computed for these models, and the models are compared when the ROCCONTRAST statement is specified. The ROC comparisons are performed by using a contrast matrix to take differences of the areas under
the empirical ROC curves (DeLong, DeLong, and Clarke-Pearson, 1988). For example, if you have three curves and the second curve is the reference, the contrast used for the overall test is
in the preceding discussion. Association statistics are computed for these models, and the models are compared when the ROCCONTRAST statement is specified. The ROC comparisons are performed by using a contrast matrix to take differences of the areas under
the empirical ROC curves (DeLong, DeLong, and Clarke-Pearson, 1988). For example, if you have three curves and the second curve is the reference, the contrast used for the overall test is
|
|
and you can optionally estimate and test each row of this contrast, in order to test the difference between the reference curve and each of the other curves. If you do not want to use a reference curve, the global test optionally uses the following contrast:
|
|
You can also specify your own contrast matrix. Instead of estimating the rows of these contrasts, you can request that the difference between every pair of ROC curves be estimated and tested.
By default for the reference contrast, the specified or selected model is used as the reference unless the NOFIT option is specified in the MODEL statement, in which case the first ROC model is the reference.
In order to label the contrasts, a name is attached to every model. The name for the specified or selected model is the MODEL statement label, or “Model” if the MODEL label is not present. The ROC statement models are named with their labels, or as “ROCi” for the ith ROC statement if a label is not specified. The contrast ![]() is labeled as “Reference = ModelName”, where ModelName is the reference model name, while
is labeled as “Reference = ModelName”, where ModelName is the reference model name, while ![]() is labeled “Adjacent Pairwise Differences”. The estimated rows of the contrast matrix are labeled “ModelName1 – ModelName2”. In particular, for the rows of
is labeled “Adjacent Pairwise Differences”. The estimated rows of the contrast matrix are labeled “ModelName1 – ModelName2”. In particular, for the rows of ![]() , ModelName2 is the reference model name. If you specify your own contrast matrix, then the contrast is labeled “Specified” and the ith contrast row estimates are labeled “Rowi”.
, ModelName2 is the reference model name. If you specify your own contrast matrix, then the contrast is labeled “Specified” and the ith contrast row estimates are labeled “Rowi”.
If ODS Graphics is enabled, then all ROC curves are displayed individually and are also overlaid in a final display. If a selection method is specified, then the curves produced in each step of the model selection process are overlaid onto a single plot and are labeled “Stepi”, and the selected model is displayed on a separate plot and on a plot with curves from specified ROC statements. See Example 54.8 for an example.
ROC Computations
The trapezoidal area under an empirical ROC curve is equal to the Mann-Whitney two-sample rank measure of association statistic
(a generalized U-statistic) applied to two samples, ![]() , in
, in ![]() and
and ![]() , in
, in ![]() . PROC LOGISTIC uses the predicted probabilities in place of
. PROC LOGISTIC uses the predicted probabilities in place of ![]() and
and ![]() ; however, in general any criterion could be used. Denote the frequency of observation i in
; however, in general any criterion could be used. Denote the frequency of observation i in ![]() as
as ![]() , and denote the total frequency in
, and denote the total frequency in ![]() as
as ![]() . The WEIGHTED option replaces
. The WEIGHTED option replaces ![]() with
with ![]() , where
, where ![]() is the weight of observation i in group
is the weight of observation i in group ![]() . The trapezoidal area under the curve is computed as
. The trapezoidal area under the curve is computed as
|
|
|
|
|
|
|
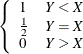 |
so that ![]() . Note that the concordance index, c, in the “Association of Predicted Probabilities and Observed Responses” table does not use weights unless both the WEIGHTED and BINWIDTH=0 options are specified. Also, in this table, c is computed by creating 500 bins and binning the
. Note that the concordance index, c, in the “Association of Predicted Probabilities and Observed Responses” table does not use weights unless both the WEIGHTED and BINWIDTH=0 options are specified. Also, in this table, c is computed by creating 500 bins and binning the ![]() and
and ![]() ; this results in more ties than the preceding method (unless the BINWIDTH=0 or ROCEPS=0 option is specified), so c is not necessarily equal to
; this results in more ties than the preceding method (unless the BINWIDTH=0 or ROCEPS=0 option is specified), so c is not necessarily equal to ![]() .
.
To compare K empirical ROC curves, first compute the trapezoidal areas. Asymptotic normality of the estimated area follows from U-statistic theory, and a covariance matrix ![]() can be computed; see DeLong, DeLong, and Clarke-Pearson (1988) for details. A Wald confidence interval for the rth area,
can be computed; see DeLong, DeLong, and Clarke-Pearson (1988) for details. A Wald confidence interval for the rth area, ![]() , can be constructed as
, can be constructed as
|
|
where ![]() is the rth diagonal of
is the rth diagonal of ![]() .
.
For a contrast of ROC curve areas, ![]() , the statistic
, the statistic
|
|
has a chi-square distribution with df=rank(![]() ). For a row of the contrast,
). For a row of the contrast, ![]() ,
,
|
|
has a standard normal distribution. The corresponding confidence interval is
|
|