The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson Regression - References
Case Deletion Diagnostic Statistics
For ordinary generalized linear models, regression diagnostic statistics developed by Williams (1987) can be requested in an output data set or in the OBSTATS table by specifying the DIAGNOSTICS | INFLUENCE option in the MODEL statement. These diagnostics measure the influence of an individual observation on model fit, and generalize the one-step diagnostics developed by Pregibon (1981) for the logistic regression model for binary data.
Preisser and Qaqish (1996) further generalized regression diagnostics to apply to models for correlated data fit by generalized estimating equations (GEEs), where the influence of entire clusters of correlated observations, or the influence of individual observations within a cluster, is measured. These diagnostic statistics can be requested in an output data set or in the OBSTATS table if a model for correlated data is specified with a REPEATED statement.
The next two sections use the following notation:
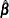
-
is the maximum likelihood estimate of the regression parameters
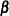 , or, in the case of correlated data, the solution of the GEEs.
, or, in the case of correlated data, the solution of the GEEs.
![$\hat{\bbeta }_{[i]}$](images/statug_genmod0555.png)
-
is the corresponding estimate evaluated with the ith observation deleted, or, in the case of correlated data, with the ith cluster deleted.
- p
-
is the dimension of the regression parameter vector
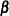 .
.

-
is the standardized Pearson residual
 , where
, where  is the variance of the ith response and
is the variance of the ith response and 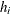 is the leverage defined in the section H | LEVERAGE.
is the leverage defined in the section H | LEVERAGE.

-
is the variance of response i,
 , where
, where  is the variance function and
is the variance function and 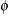 is the dispersion parameter.
is the dispersion parameter.
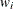
-
is the prior weight of the ith observation specified with the WEIGHT statement. If there is no WEIGHT statement,
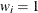 for all i.
for all i.
All unknown quantities are replaced by their estimated values in the following two sections.
Diagnostics for Ordinary Generalized Linear Models
The following statistics are available for generalized linear models.
DFBETA
The DFBETA statistic for measuring the influence of the ith observation is defined as the one-step approximation to the difference in the MLE of the regression parameter vector and the MLE of the regression parameter vector without the ith observation. This one-step approximation assumes a Fisher scoring step, and is given by
|
|
where ![]() is the leverage defined in the section H | LEVERAGE.
is the leverage defined in the section H | LEVERAGE.
DFBETAS
The standardized DFBETA statistic for assessing the influence of the ith observation on the jth regression parameter is defined as the DFBETA statistic for the jth parameter divided by its estimated standard deviation, where the standard deviation is estimated from all the data.
|
|
DOBS | COOKD | COOKSD
In normal linear regression, the influence of observation i can be measured by Cook’s distance (Cook and Weisberg, 1982). A measure of influence of observation i for generalized linear models that is equivalent to Cook’s distance for normal linear regression is given by
|
|
where ![]() is the leverage defined in the section H | LEVERAGE. This measure is the one-step approximation to
is the leverage defined in the section H | LEVERAGE. This measure is the one-step approximation to ![]() , where
, where ![]() is the log likelihood evaluated at
is the log likelihood evaluated at ![]() .
.
H | LEVERAGE
The Fisher scores, or expected, weight for observation i is ![]() . Let
. Let ![]() be the diagonal matrix with
be the diagonal matrix with ![]() as the ith diagonal. The leverage
as the ith diagonal. The leverage ![]() of the ith observation is defined as the ith diagonal element of the hat matrix
of the ith observation is defined as the ith diagonal element of the hat matrix
|
|
Diagnostics for Models Fit by Generalized Estimating Equations (GEEs)
The diagnostic statistics in this section were developed by Preisser and Qaqish (1996). See the section Generalized Estimating Equations for further information and notation for generalized estimating equations (GEEs). The following additional notation is used in this section.
Partition the design matrix ![]() and response vector
and response vector ![]() by cluster; that is, let
by cluster; that is, let ![]() , and
, and ![]() corresponding to the K clusters.
corresponding to the K clusters.
Let ![]() be the number of responses for cluster i, and denote by
be the number of responses for cluster i, and denote by ![]() the total number of observations. Denote by
the total number of observations. Denote by ![]() the
the ![]() diagonal matrix with
diagonal matrix with ![]() as the jth diagonal element. If there is a WEIGHT statement, the diagonal element of
as the jth diagonal element. If there is a WEIGHT statement, the diagonal element of ![]() is
is ![]() , where
, where ![]() is the specified weight of the jth observation in the ith cluster. Let
is the specified weight of the jth observation in the ith cluster. Let ![]() the
the ![]() diagonal matrix with
diagonal matrix with ![]() as diagonal elements,
as diagonal elements, ![]() ,
, ![]() . Let
. Let ![]() the
the ![]() diagonal matrix corresponding to cluster i with
diagonal matrix corresponding to cluster i with ![]() as the jth diagonal element.
as the jth diagonal element.
Let ![]() be the
be the ![]() block diagonal weight matrix whose ith block, corresponding to the ith cluster, is the
block diagonal weight matrix whose ith block, corresponding to the ith cluster, is the ![]() matrix
matrix
|
|
where ![]() is the working correlation matrix for cluster i.
is the working correlation matrix for cluster i.
Let
|
|
where ![]() is the
is the ![]() design matrix corresponding to cluster i.
design matrix corresponding to cluster i.
Define the adjusted residual vector as
|
|
and ![]() , the estimated residual for the ith cluster.
, the estimated residual for the ith cluster.
Let the subscript ![]() denote estimates evaluated without the ith cluster,
denote estimates evaluated without the ith cluster, ![]() estimates evaluated using all the data except the tth observation of the ith cluster, and let
estimates evaluated using all the data except the tth observation of the ith cluster, and let ![]() denote matrices corresponding to the ith cluster without the tth observation.
denote matrices corresponding to the ith cluster without the tth observation.
The following statistics are available for generalized estimating equation models.
CH | CLUSTERH | CLEVERAGE
The leverage of cluster i is contained in the matrix ![]() , and is summarized by the trace of
, and is summarized by the trace of ![]() ,
,
|
|
The leverage ![]() of the tth observation in the ith cluster is the tth diagonal element of
of the tth observation in the ith cluster is the tth diagonal element of ![]() .
.
DFBETAC
The effect of deleting cluster i on the estimated parameter vector is given by the following one-step approximation for ![]() :
:
|
|
DFBETACS
The cluster deletion statistic DFBETAC can be standardized using the variances of ![]() based on the complete data. The standardized one-step approximation for the change in
based on the complete data. The standardized one-step approximation for the change in ![]() due to deletion of cluster i is
due to deletion of cluster i is
|
|
DFBETAO
Partition the matrices ![]() and
and ![]() as
as
|
|
|
|
and let ![]() and
and ![]() .
.
The effect of deleting the tth observation from the ith cluster is given by the following one-step approximation to ![]() :
:
|
|
where ![]() ,
, ![]() , and
, and ![]() . Note that
. Note that ![]() ,
, ![]() , and
, and ![]() are scalars.
are scalars.
DFBETAOS
The observation deletion statistic DFBETAO can be standardized using the variances of ![]() based on the complete data. The standardized one-step approximation for the change in
based on the complete data. The standardized one-step approximation for the change in ![]() due to deletion of observation t in cluster i is
due to deletion of observation t in cluster i is
|
|
DCLS | CLUSTERCOOKD | CLUSTERCOOKSD
A measure of the standardized influence of the subset m of observations on the overall fit is ![]() . For deletion of cluster i, this is approximated by
. For deletion of cluster i, this is approximated by
|
|
DOBS | COOKD | COOKSD
The measure of overall fit in the section DCLS | CLUSTERCOOKD | CLUSTERCOOKSD for the deletion of the tth observation in the ith cluster is approximated by
|
|
where ![]() ,
, ![]() , and
, and ![]() are defined in the section DFBETAO. In the case of the independence working correlation, this is equal to the measure for ordinary generalized linear models
defined in the section DOBS | COOKD | COOKSD.
are defined in the section DFBETAO. In the case of the independence working correlation, this is equal to the measure for ordinary generalized linear models
defined in the section DOBS | COOKD | COOKSD.
MCLS | CLUSTERDFIT
A studentized distance measure of the type defined in the section DCLS | CLUSTERCOOKD | CLUSTERCOOKSD of the influence of the ith cluster is given by
|
|