The ANOVA Procedure
One-Way Layout with Means Comparisons
A one-way analysis of variance considers one treatment factor with two or more treatment levels. The goal of the analysis is to test for differences among the means of the levels and to quantify these differences. If there are two treatment levels, this analysis is equivalent to a t test comparing two group means.
The assumptions of analysis of variance (Steel and Torrie, 1980) are that treatment effects are additive and experimental errors are independently random with a normal distribution that has mean zero and constant variance.
The following example studies the effect of bacteria on the nitrogen content of red clover plants. The treatment factor is
bacteria strain, and it has six levels. Five of the six levels consist of five different Rhizobium trifolii bacteria cultures combined with a composite of five Rhizobium meliloti strains. The sixth level is a composite of the five Rhizobium trifolii strains with the composite of the Rhizobium meliloti. Red clover plants are inoculated with the treatments, and nitrogen content is later measured in milligrams. The data are
derived from an experiment by Erdman (1946) and are analyzed in Chapters 7 and 8 of Steel and Torrie (1980). The following DATA step creates the SAS data set Clover:
title1 'Nitrogen Content of Red Clover Plants'; data Clover; input Strain $ Nitrogen @@; datalines; 3DOK1 19.4 3DOK1 32.6 3DOK1 27.0 3DOK1 32.1 3DOK1 33.0 3DOK5 17.7 3DOK5 24.8 3DOK5 27.9 3DOK5 25.2 3DOK5 24.3 3DOK4 17.0 3DOK4 19.4 3DOK4 9.1 3DOK4 11.9 3DOK4 15.8 3DOK7 20.7 3DOK7 21.0 3DOK7 20.5 3DOK7 18.8 3DOK7 18.6 3DOK13 14.3 3DOK13 14.4 3DOK13 11.8 3DOK13 11.6 3DOK13 14.2 COMPOS 17.3 COMPOS 19.4 COMPOS 19.1 COMPOS 16.9 COMPOS 20.8 ;
The variable Strain contains the treatment levels, and the variable Nitrogen contains the response. The following statements produce the analysis.
proc anova data = Clover; class strain; model Nitrogen = Strain; run;
The classification variable is specified in the CLASS statement. Note that, unlike the GLM procedure, PROC ANOVA does not allow continuous variables on the right-hand side of the model. Figure 25.1 and Figure 25.2 display the output produced by these statements.
Figure 25.1: Class Level Information
| Nitrogen Content of Red Clover Plants |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| Strain | 6 | 3DOK1 3DOK13 3DOK4 3DOK5 3DOK7 COMPOS |
| Number of Observations Read | 30 |
|---|---|
| Number of Observations Used | 30 |
The “Class Level Information” table shown in Figure 25.1 lists the variables that appear in the CLASS statement, their levels, and the number of observations in the data set.
Figure 25.2 displays the ANOVA table, followed by some simple statistics and tests of effects.
Figure 25.2: ANOVA Table
| Nitrogen Content of Red Clover Plants |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 5 | 847.046667 | 169.409333 | 14.37 | <.0001 |
| Error | 24 | 282.928000 | 11.788667 | ||
| Corrected Total | 29 | 1129.974667 |
| R-Square | Coeff Var | Root MSE | Nitrogen Mean |
|---|---|---|---|
| 0.749616 | 17.26515 | 3.433463 | 19.88667 |
| Source | DF | Anova SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Strain | 5 | 847.0466667 | 169.4093333 | 14.37 | <.0001 |
The degrees of freedom (DF) column should be used to check the analysis results. The model degrees of freedom for a one-way analysis of variance are the number of levels minus 1; in this case, 6 – 1 = 5. The Corrected Total degrees of freedom are always the total number of observations minus one; in this case 30 – 1 = 29. The sum of Model and Error degrees of freedom equals the Corrected Total.
The overall F test is significant ![]() , indicating that the model as a whole accounts for a significant portion of the variability in the dependent variable. The
F test for
, indicating that the model as a whole accounts for a significant portion of the variability in the dependent variable. The
F test for Strain is significant, indicating that some contrast between the means for the different strains is different from zero. Notice
that the Model and Strain F tests are identical, since Strain is the only term in the model.
The F test for Strain ![]() suggests that there are differences among the bacterial strains, but it does not reveal any information about the nature
of the differences. Mean comparison methods can be used to gather further information. The interactivity of PROC ANOVA enables
you to do this without re-running the entire analysis. After you specify a model with a MODEL statement and execute the ANOVA procedure with a RUN statement, you can execute a variety of statements (such as MEANS, MANOVA, TEST, and REPEATED) without PROC ANOVA recalculating the model sum of squares.
suggests that there are differences among the bacterial strains, but it does not reveal any information about the nature
of the differences. Mean comparison methods can be used to gather further information. The interactivity of PROC ANOVA enables
you to do this without re-running the entire analysis. After you specify a model with a MODEL statement and execute the ANOVA procedure with a RUN statement, you can execute a variety of statements (such as MEANS, MANOVA, TEST, and REPEATED) without PROC ANOVA recalculating the model sum of squares.
The following additional statements request means of the Strain levels with Tukey’s studentized range procedure.
means strain / tukey; run;
Results of Tukey’s procedure are shown in Figure 25.3.
Figure 25.3: Tukey’s Multiple Comparisons Procedure
| Nitrogen Content of Red Clover Plants |
| Alpha | 0.05 |
|---|---|
| Error Degrees of Freedom | 24 |
| Error Mean Square | 11.78867 |
| Critical Value of Studentized Range | 4.37265 |
| Minimum Significant Difference | 6.7142 |
| Means with the same letter are not significantly different. |
||||
|---|---|---|---|---|
| Tukey Grouping | Mean | N | Strain | |
| A | 28.820 | 5 | 3DOK1 | |
| A | ||||
| B | A | 23.980 | 5 | 3DOK5 |
| B | ||||
| B | C | 19.920 | 5 | 3DOK7 |
| B | C | |||
| B | C | 18.700 | 5 | COMPOS |
| C | ||||
| C | 14.640 | 5 | 3DOK4 | |
| C | ||||
| C | 13.260 | 5 | 3DOK13 | |
Examples of implications of the multiple comparisons results are as follows:
-
Strain 3DOK1 fixes significantly more nitrogen than all but 3DOK5.
-
While 3DOK5 is not significantly different from 3DOK1, it is also not significantly better than all the rest, though it is better than the bottom two groups.
Although the experiment has succeeded in separating the best strains from the worst, more experimentation is required in order to clearly distinguish the very best strain.
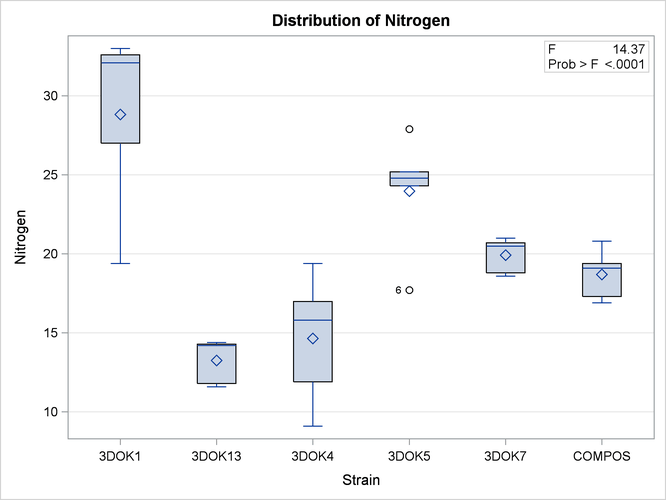
If ODS Graphics is enabled, ANOVA also displays by default a plot that enables you to visualize the distribution of nitrogen content for each treatment. The following statements, which are the same as the previous analysis but with ODS graphics enabled, additionally produce Figure 25.4.
ods graphics on; proc anova data = Clover; class strain; model Nitrogen = Strain; run; ods graphics off;
When ODS Graphics is enabled and you fit a one-way analysis of variance model, the ANOVA procedure output includes a box plot of the dependent variable values within each classification level of the independent variable. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the graphics available in the ANOVA procedure, see the section ODS Graphics.
Figure 25.4: Box Plot of Nitrogen Content for each Treatment