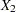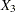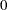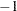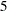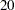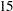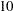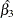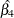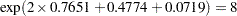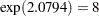The SURVEYLOGISTIC Procedure

Odds Ratio Estimation

Consider a dichotomous response variable with outcomes event and nonevent. Let a dichotomous risk factor variable X take the value 1 if the risk factor is present and 0 if the risk factor is absent. According to the logistic model, the log odds function, , is given by

The odds ratio 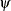is defined as the ratio of the odds for those with the risk factor (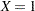) to the odds for those without the risk factor (). The log of the odds ratio is given by

The parameter, 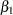, associated with 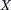represents the change in the log odds from to 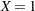. So the odds ratio is obtained by simply exponentiating the value of the parameter associated with the risk factor. The odds ratio indicates how the odds of event change as you change 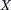from 0 to 1. For instance, 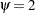means that the odds of an event when 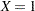are twice the odds of an event when .

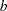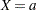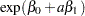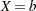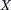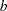Suppose the values of the dichotomous risk factor are coded as constants and instead of 0 and 1. The odds when become , and the odds when become . The odds ratio corresponding to an increase in from to is

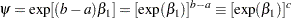Note that for any and 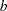such that 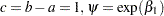. So the odds ratio can be interpreted as the change in the odds for any increase of one unit in the corresponding risk factor. However, the change in odds for some amount other than one unit is often of greater interest. For example, a change of one pound in body weight might be too small to be considered important, while a change of 10 pounds might be more meaningful. The odds ratio for a change in 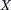from to 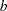is estimated by raising the odds ratio estimate for a unit change in 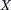to the power of , as shown previously.

For a polytomous risk factor, the computation of odds ratios depends on how the risk factor is parameterized. For illustration, suppose that Race is a risk factor with four categories: White, Black, Hispanic, and Other.

For the effect parameterization scheme (PARAM=EFFECT) with White as the reference group, the design variables for Race are as follows.

The log odds for Black is

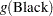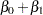The log odds for White is

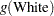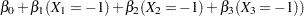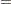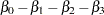Therefore, the log odds ratio of Black versus White becomes

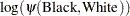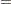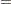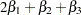For the reference cell parameterization scheme (PARAM=REF) with White as the reference cell, the design variables for race are as follows.

The log odds ratio of Black versus White is given by

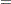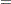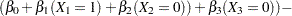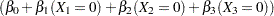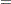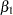For the GLM parameterization scheme (PARAM=GLM), the design variables are as follows.

The log odds ratio of Black versus White is

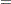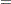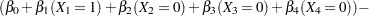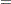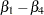Consider the hypothetical example of heart disease among race in Hosmer and Lemeshow (2000, p. 51). The entries in the following contingency table represent counts.

The computation of odds ratio of Black versus White for various parameterization schemes is shown in Table 87.7.

Since the log odds ratio (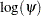) is a linear function of the parameters, the Wald confidence interval for 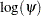can be derived from the parameter estimates and the estimated covariance matrix. Confidence intervals for the odds ratios are obtained by exponentiating the corresponding confidence intervals for the log odd ratios. In the displayed output of PROC SURVEYLOGISTIC, the "Odds Ratio Estimates" table contains the odds ratio estimates and the corresponding 95% Wald confidence intervals computed by using the covariance matrix in the section Variance Estimation. For continuous explanatory variables, these odds ratios correspond to a unit increase in the risk factors.

To customize odds ratios for specific units of change for a continuous risk factor, you can use the UNITS statement to specify a list of relevant units for each explanatory variable in the model. Estimates of these customized odds ratios are given in a separate table. Let be a confidence interval for 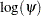. 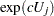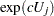The corresponding lower and upper confidence limits for the customized odds ratio are and , respectively, (for ); or and , respectively, (for ). You use the CLODDS option in the MODEL statement to request confidence intervals for the odds ratios.

For a generalized logit model, odds ratios are computed similarly, except 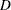odds ratios are computed for each effect, corresponding to the 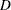logits in the model.