Overview: SURVEYLOGISTIC Procedure

Categorical responses arise extensively in sample survey. Common examples of responses include the following:

• binary: for example, attended graduate school or not

• ordinal: for example, mild, moderate, and severe pain

• nominal: for example, ABC, NBC, CBS, FOX TV network viewed at a certain hour

Logistic regression analysis is often used to investigate the relationship between such discrete responses and a set of explanatory variables. See Binder (1981, 1983); Roberts, Rao, and Kumar (1987); Skinner, Holt, and Smith (1989); Morel (1989); and Lehtonen and Pahkinen (1995) for description of logistic regression for sample survey data.

For binary response models, the response of a sampling unit can take a specified value or not (for example, attended graduate school or not). Suppose is a row vector of explanatory variables and is the response probability to be modeled. The linear logistic model has the form

where is the intercept parameter and 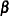is the vector of slope parameters.

The logistic model shares a common feature with the more general class of generalized linear models—namely, that a function of the expected value, 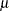, of the response variable is assumed to be linearly related to the explanatory variables. Since 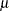implicitly depends on the stochastic behavior of the response, and since t he explanatory variables are assumed to be fixed, the function provides the link between the random (stochastic) component and the systematic (deterministic) component of the response variable. For this reason, Nelder and Wedderburn (1972) refer to 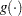as a link function. One advantage of the logit function over other link functions is that differences on the logistic scale are interpretable regardless of whether the data are sampled prospectively or retrospectively (McCullagh and Nelder 1989, Chapter 4). Other link functions that are widely used in practice are the probit function and the complementary log-log function. The SURVEYLOGISTIC  procedure enables you to choose one of these link functions, resulting in fitting a broad class of binary response models of the form

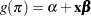For ordinal response models, the response 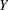of an individual or an experimental unit might be restricted to one of a usually small number of ordinal values, denoted for convenience by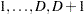 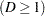. For example, pain severity can be classified into three response categories as 1=mild, 2=moderate, and 3=severe. The SURVEYLOGISTIC  procedure fits a common slopes cumulative model, which is a parallel lines regression model based on the cumulative probabilities of the response categories rather than on their individual probabilities. The cumulative model has the form

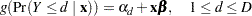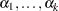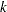where are intercept parameters and 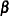is the vector of slope parameters. This model has been considered by many researchers. Aitchison and Silvey (1957) and Ashford (1959) employ a probit scale and provide a maximum likelihood analysis; Walker and Duncan (1967) and Cox and Snell (1989) discuss the use of the log-odds scale. For the log-odds scale, the cumulative logit model is often referred to as the proportional odds model.

For nominal response logistic models, where the 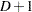possible responses have no natural ordering, the logit model can also be extended to a generalized logit model, which has the form

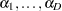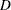where the are intercept parameters and the are 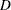vectors of parameters. These models were introduced by McFadden (1974) as the discrete choice model, and they are also known as multinomial models.

The SURVEYLOGISTIC  procedure fits linear logistic regression models for discrete response survey data by the method of maximum likelihood. For statistical inferences, PROC SURVEYLOGISTIC  incorporates complex survey sample designs, including designs with stratification, clustering, and unequal weighting.

The maximum likelihood estimation is carried out with either the Fisher scoring algorithm or the Newton-Raphson algorithm. You can specify starting values for the parameter estimates. The logit link function in the ordinal logistic regression models can be replaced by the probit function or the complementary log-log function.

Odds ratio estimates are displayed along with parameter estimates. You can also specify the change in the explanatory variables for which odds ratio estimates are desired.

Variances of the regression parameters and odds ratios are computed by using either the Taylor series (linearization) method or replication (resampling) methods to estimate sampling errors of estimators based on complex sample designs (Binder 1983; Särndal, Swensson, and Wretman 1992, Wolter 2007; Rao, Wu, and Yue 1992).

The SURVEYLOGISTIC  procedure enables you to specify categorical variables (also known as CLASS variables) as explanatory variables. It also enables you to specify interaction terms in the same way as in the LOGISTIC procedure.

Like many procedures in SAS/STAT software that allow the specification of CLASS variables, the SURVEYLOGISTIC  procedure provides a CONTRAST statement for specifying customized hypothesis tests concerning the model parameters. The CONTRAST statement also provides estimation of individual rows of contrasts, which is particularly useful for obtaining odds ratio estimates for various levels of the CLASS variables.