The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC Statement BY Statement CLASS Statement CLUSTER Statement CONTRAST Statement DOMAIN Statement EFFECT Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement
PROC SURVEYLOGISTIC Statement BY Statement CLASS Statement CLUSTER Statement CONTRAST Statement DOMAIN Statement EFFECT Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
 Missing Values Model Specification Model Fitting Survey Design Information Logistic Regression Models and Parameters Variance Estimation Domain Analysis Hypothesis Testing and Estimation Linear Predictor, Predicted Probability, and Confidence Limits Output Data Sets Displayed Output ODS Table Names ODS Graphics
Missing Values Model Specification Model Fitting Survey Design Information Logistic Regression Models and Parameters Variance Estimation Domain Analysis Hypothesis Testing and Estimation Linear Predictor, Predicted Probability, and Confidence Limits Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples

- References
| CONTRAST Statement |
- CONTRAST ’label’ row-description <, ... , row-description </ options>> ;
effect values <,  , effect values>
, effect values>
The CONTRAST statement provides a mechanism for obtaining customized hypothesis tests. It is similar to the CONTRAST statement in PROC LOGISTIC and PROC GLM, depending on the coding schemes used with any classification variables involved.
The CONTRAST statement enables you to specify a matrix, 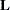 , for testing the hypothesis
, for testing the hypothesis  , where
, where 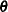 is the parameter vector. You must be familiar with the details of the model parameterization that PROC SURVEYLOGISTIC uses (for more information, see the PARAM= option in the section CLASS Statement). Optionally, the CONTRAST statement enables you to estimate each row,
is the parameter vector. You must be familiar with the details of the model parameterization that PROC SURVEYLOGISTIC uses (for more information, see the PARAM= option in the section CLASS Statement). Optionally, the CONTRAST statement enables you to estimate each row, 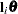 , of
, of  and test the hypothesis
and test the hypothesis  . Computed statistics are based on the asymptotic chi-square distribution of the Wald statistic.
. Computed statistics are based on the asymptotic chi-square distribution of the Wald statistic.
There is no limit to the number of CONTRAST statements that you can specify, but they must appear after the MODEL statement.
The following parameters can be specified in the CONTRAST statement:
- label
identifies the contrast on the output. A label is required for every contrast specified, and it must be enclosed in quotes.
- effect
identifies an effect that appears in the MODEL statement. The name INTERCEPT can be used as an effect when one or more intercepts are included in the model. You do not need to include all effects that are included in the MODEL statement.
- values
are constants that are elements of the
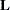 matrix associated with the effect. To correctly specify your contrast, it is crucial to know the ordering of parameters within each effect and the variable levels associated with any parameter. The "Class Level Information" table shows the ordering of levels within variables. The E option, described later in this section, enables you to verify the proper correspondence of values to parameters.
matrix associated with the effect. To correctly specify your contrast, it is crucial to know the ordering of parameters within each effect and the variable levels associated with any parameter. The "Class Level Information" table shows the ordering of levels within variables. The E option, described later in this section, enables you to verify the proper correspondence of values to parameters.
The rows of 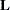 are specified in order and are separated by commas. Multiple degree-of-freedom hypotheses can be tested by specifying multiple row-descriptions. For any of the full-rank parameterizations, if an effect is not specified in the CONTRAST statement, all of its coefficients in the
are specified in order and are separated by commas. Multiple degree-of-freedom hypotheses can be tested by specifying multiple row-descriptions. For any of the full-rank parameterizations, if an effect is not specified in the CONTRAST statement, all of its coefficients in the 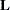 matrix are set to 0. If too many values are specified for an effect, the extra ones are ignored. If too few values are specified, the remaining ones are set to 0.
matrix are set to 0. If too many values are specified for an effect, the extra ones are ignored. If too few values are specified, the remaining ones are set to 0.
When you use effect coding (by default or by specifying PARAM=EFFECT in the CLASS statement), all parameters are directly estimable (involve no other parameters).
For example, suppose an effect that is coded CLASS variable A has four levels. Then there are three parameters ( ) that represent the first three levels, and the fourth parameter is represented by
) that represent the first three levels, and the fourth parameter is represented by
 |
To test the first versus the fourth level of A, you would test
 |
or, equivalently,
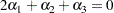 |
which, in the form  , is
, is
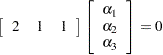 |
Therefore, you would use the following CONTRAST statement:
contrast '1 vs. 4' A 2 1 1;
To contrast the third level with the average of the first two levels, you would test
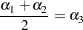 |
or, equivalently,
 |
Therefore, you would use the following CONTRAST statement:
contrast '1&2 vs. 3' A 1 1 -2;
Other CONTRAST statements are constructed similarly. For example:
contrast '1 vs. 2 ' A 1 -1 0;
contrast '1&2 vs. 4 ' A 3 3 2;
contrast '1&2 vs. 3&4' A 2 2 0;
contrast 'Main Effect' A 1 0 0,
A 0 1 0,
A 0 0 1;
When you use the less-than-full-rank parameterization (by specifying PARAM=GLM in the CLASS statement), each row is checked for estimability. If PROC SURVEYLOGISTIC finds a contrast to be nonestimable, it displays missing values in corresponding rows in the results. PROC SURVEYLOGISTIC handles missing level combinations of classification variables in the same manner as PROC LOGISTIC. Parameters corresponding to missing level combinations are not included in the model. This convention can affect the way in which you specify the 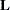 matrix in your CONTRAST statement. If the elements of
matrix in your CONTRAST statement. If the elements of 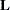 are not specified for an effect that contains a specified effect, then the elements of the specified effect are distributed over the levels of the higher-order effect just as the LOGISTIC procedure does for its CONTRAST and ESTIMATE statements. For example, suppose that the model contains effects A and B and their interaction A*B. If you specify a CONTRAST statement involving A alone, the
are not specified for an effect that contains a specified effect, then the elements of the specified effect are distributed over the levels of the higher-order effect just as the LOGISTIC procedure does for its CONTRAST and ESTIMATE statements. For example, suppose that the model contains effects A and B and their interaction A*B. If you specify a CONTRAST statement involving A alone, the 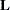 matrix contains nonzero terms for both A and A*B, since A*B contains A.
matrix contains nonzero terms for both A and A*B, since A*B contains A.
The degrees of freedom is the number of linearly independent constraints implied by the CONTRAST statement—that is, the rank of 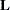 .
.
You can specify the following options after a slash (/):
- ALPHA=value
sets the confidence level for confidence limits. The value of the ALPHA= option must be between 0 and 1, and the default value is 0.05. A confidence level of
 produces
produces  % confidence limits. The default of ALPHA=0.05 produces 95% confidence limits.
% confidence limits. The default of ALPHA=0.05 produces 95% confidence limits. - E
- ESTIMATE=keyword
-
requests that each individual contrast (that is, each row,
 , of
, of  ) or exponentiated contrast (
) or exponentiated contrast ( ) be estimated and tested. PROC SURVEYLOGISTIC displays the point estimate, its standard error, a Wald confidence interval, and a Wald chi-square test for each contrast. The significance level of the confidence interval is controlled by the ALPHA= option. You can estimate the contrast or the exponentiated contrast (
) be estimated and tested. PROC SURVEYLOGISTIC displays the point estimate, its standard error, a Wald confidence interval, and a Wald chi-square test for each contrast. The significance level of the confidence interval is controlled by the ALPHA= option. You can estimate the contrast or the exponentiated contrast ( ), or both, by specifying one of the following keywords:
), or both, by specifying one of the following keywords: - PARM
specifies that the contrast itself be estimated
- EXP
specifies that the exponentiated contrast be estimated
- BOTH
specifies that both the contrast and the exponentiated contrast be estimated
- SINGULAR=value
-
tunes the estimability checking. If
 is a vector, define ABS(
is a vector, define ABS( ) to be the largest absolute value of the elements of
) to be the largest absolute value of the elements of  . For a row vector
. For a row vector  of the matrix
of the matrix 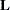 , define
, define 
If ABS(
 ) is greater than
) is greater than  *value, then
*value, then 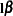 is declared nonestimable. The
is declared nonestimable. The  matrix is the Hermite form matrix
matrix is the Hermite form matrix  , where
, where  represents a generalized inverse of the information matrix
represents a generalized inverse of the information matrix 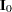 of the null model. The value must be between 0 and 1; the default is
of the null model. The value must be between 0 and 1; the default is  .
.