The PROBIT Procedure
- Overview
-
Getting Started
-
Syntax
-
Details
Missing Values Response Level Ordering Computational Method Distributions INEST= SAS-data-set Model Specification Lack-of-Fit Tests Rescaling the Covariance Matrix Tolerance Distribution Inverse Confidence Limits OUTEST= SAS-data-set XDATA= SAS-data-set Traditional High-Resolution Graphics Displayed Output ODS Table Names ODS Graphics
-
Examples
- References
| Lack-of-Fit Tests |
Two goodness-of-fit tests can be requested from the PROBIT procedure: a Pearson’s chi-square test and a log-likelihood ratio chi-square test.
To compute the test statistics, you can use the AGGREGATE or AGGREGATE= option grouping the observations into subpopulations. If neither AGGREGATE nor AGGREGATE= is specified, PROC PROBIT assumes that each observation is from a separate subpopulation and computes the goodness-of-fit test statistics only for the events/trials syntax.
If the Pearson’s goodness-of-fit chi-square test is requested and the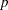 
-value for the test is too small, variances and covariances are adjusted by a heterogeneity factor (the goodness-of-fit chi-square divided by its degrees of freedom) and a critical value from the 
distribution is used to compute the fiducial limits. The Pearson’s chi-square test statistic is computed as
 |
where the sum on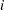 
is over grouping, the sum on 
is over levels of response, 
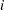is the frequency of response level for the th grouping, 
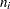is the total frequency for the 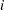th grouping, and 
is the fitted probability for the th level at the 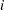th grouping.
The likelihood ratio chi-square test statistic is computed as
 |
This quantity is sometimes called the deviance. If the modeled probabilities fit the data, these statistics should be approximately distributed as chi-square with degrees of freedom equal to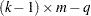 
, where 
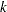is the number of levels of the multinomial or binomial response, 
is the number of sets of independent variable values (covariate patterns), and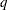 
is the number of parameters fit in the model.
In order for the Pearson’s statistic and the deviance to be distributed as chi-square, there must be sufficient replication within the groupings. When this is not true, the data are sparse, and the 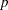-values for these statistics are not valid and should be ignored. Similarly, these statistics, divided by their degrees of freedom, cannot serve as indicators of overdispersion. A large difference between the Pearson’s statistic and the deviance provides some evidence that the data are too sparse to use either statistic.