The HPMIXED Procedure
| Computing Starting Values by EM-REML |
The EM-REML algorithm (Dempster, Laird, and Rubin; 1977) iteratively alternates between an expectation step and a maximization step to maximize the restricted log likelihood. The algorithm is based on augmenting the observed data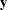 
with the unobservable random effects 
, leading to a simplified form for the log likelihood. For example, if 
then given the realized values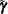 
of the unobservable random effects , the REML estimate of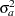 
satisfies
 |
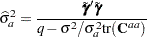This corresponds to the maximization step of EM-REML. However, the true realized values 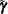are unknown in practice. The expectation step of EM-REML replaces them with the conditional expected values 
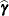of the random effects, given the observed data 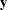and initial values for the parameters. The new estimate of 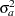is used in turn to recalculate the conditional expected values, and the iteration is repeated until convergence.
It is well known that EM-REML is generally more robust against a poor choice of starting values than general nonlinear optimization methods such as Newton-Raphson, though it tends to converge slowly as it approaches the optimum. The Newton-Raphson method, on the other hand, converges much faster when it has a good set of starting values. The HPMIXED procedure, thus, employs a scheme that uses EM-REML initially in order to get good starting values, and after a few iterations, when the decrease in log likelihood has significantly slowed down, switching to a more general nonlinear optimization technique (by default, quasi-Newton).