The HPMIXED Procedure
| Model Assumptions |
The following sections provide an overview of the approach used by the HPMIXED procedure for likelihood-based analysis of linear mixed models with sparse matrix technique. Additional theory and examples are provided in Littell et al. (1996), Verbeke and Molenberghs (1997, 2000), and Brown and Prescott (1999).
The HPMIXED procedure fits models generally of the form
 |
Models of this form contain both fixed-effects parameters, 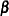 , and random-effects parameters,
, and random-effects parameters,  ; hence, they are called mixed models. Refer to Henderson (1990) and Searle, Casella, and McCulloch (1992) for historical developments of the mixed model. Note that the matrix
; hence, they are called mixed models. Refer to Henderson (1990) and Searle, Casella, and McCulloch (1992) for historical developments of the mixed model. Note that the matrix 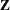 can contain either continuous or dummy variables, just like
can contain either continuous or dummy variables, just like 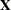 .
.
So far this is the same general form of model fit by the MIXED procedure. The difference between the models handled by the two procedures lies in the assumptions about the distributions of  and
and  . For both procedures a key assumption is that
. For both procedures a key assumption is that  and
and  are normally distributed with
are normally distributed with
 |
 |
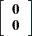 |
|||
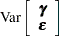 |
 |
 |
The two procedures differ in their assumptions about the variance matrices 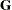 and
and  for
for  and
and  , respectively. The MIXED procedure allows a variety of different structures for both
, respectively. The MIXED procedure allows a variety of different structures for both 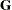 and
and  ; while in HPMIXED procedure,
; while in HPMIXED procedure,  is always assumed to be of the form
is always assumed to be of the form 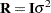 , and the structures available for modeling
, and the structures available for modeling 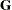 are only a small subset of the structures offered by the MIXED procedure.
are only a small subset of the structures offered by the MIXED procedure.
Estimates of fixed effects and predictions for random effects are obtained by solving the so-called mixed model equations:
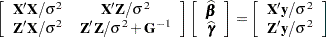 |
Let 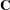 denote the coefficient matrix of the mixed model equations:
denote the coefficient matrix of the mixed model equations:
 |
Under the assumptions given previously for the moments of  and
and  , the variance of
, the variance of 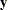 is
is 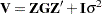 . You can model
. You can model 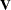 by setting up the random-effects design matrix
by setting up the random-effects design matrix 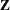 and by specifying covariance structures for
and by specifying covariance structures for 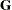 . Let
. Let 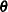 be a vector of all unknown parameters in
be a vector of all unknown parameters in 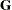 . Then the general form of the restricted likelihood function for the mixed models that the HPMIXED procedure can fit is
. Then the general form of the restricted likelihood function for the mixed models that the HPMIXED procedure can fit is
 |
where
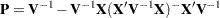 |
and 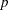 is the rank of
is the rank of 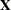 . The HPMIXED procedure minimizes
. The HPMIXED procedure minimizes 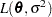 over all unknown parameters in
over all unknown parameters in 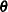 and
and  by using nonlinear optimization algorithms.
by using nonlinear optimization algorithms.
