The GLIMMIX Procedure
-
Overview
-
Getting Started
-
Syntax
PROC GLIMMIX Statement BY Statement CLASS Statement CONTRAST Statement COVTEST Statement EFFECT Statement ESTIMATE Statement FREQ Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement NLOPTIONS Statement OUTPUT Statement PARMS Statement RANDOM Statement SLICE Statement STORE Statement WEIGHT Statement Programming Statements User-Defined Link or Variance Function
-
Details
Generalized Linear Models Theory Generalized Linear Mixed Models Theory GLM Mode or GLMM Mode Statistical Inference for Covariance Parameters Satterthwaite Degrees of Freedom Approximation Empirical Covariance (Sandwich) Estimators Exploring and Comparing Covariance Matrices Processing by Subjects Radial Smoothing Based on Mixed Models Odds and Odds Ratio Estimation Parameterization of Generalized Linear Mixed Models Response-Level Ordering and Referencing Comparing the GLIMMIX and MIXED Procedures Singly or Doubly Iterative Fitting Default Estimation Techniques Default Output Notes on Output Statistics ODS Table Names ODS Graphics
-
Examples
Binomial Counts in Randomized Blocks Mating Experiment with Crossed Random Effects Smoothing Disease Rates; Standardized Mortality Ratios Quasi-likelihood Estimation for Proportions with Unknown Distribution Joint Modeling of Binary and Count Data Radial Smoothing of Repeated Measures Data Isotonic Contrasts for Ordered Alternatives Adjusted Covariance Matrices of Fixed Effects Testing Equality of Covariance and Correlation Matrices Multiple Trends Correspond to Multiple Extrema in Profile Likelihoods Maximum Likelihood in Proportional Odds Model with Random Effects Fitting a Marginal (GEE-Type) Model Response Surface Comparisons with Multiplicity Adjustments Generalized Poisson Mixed Model for Overdispersed Count Data Comparing Multiple B-Splines Diallel Experiment with Multimember Random Effects Linear Inference Based on Summary Data
- References
| Satterthwaite Degrees of Freedom Approximation |
The DDFM=SATTERTHWAITE option in the MODEL statement requests denominator degrees of freedom in 
tests and 
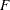tests computed according to a general Satterthwaite approximation. The DDFM=KENWARDROGER option also entails the computation of Satterthwaite-type degrees of freedom.
The general Satterthwaite approximation computed in PROC GLIMMIX for the test
 |
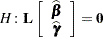is based on the 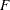statistic
 |
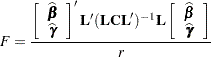where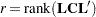 
, and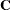 
is the approximate variance matrix of 
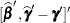; see the section Estimated Precision of Estimates and the section Aspects Common to Adaptive Quadrature and Laplace Approximation.
The approximation proceeds by first performing the spectral decomposition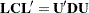 
, where 
is an orthogonal matrix of eigenvectors and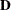 
is a diagonal matrix of eigenvalues, both of dimension 
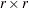. Define 
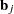to be the 
th row of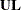 
, and let
 |
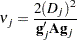where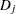 
is the th diagonal element of 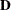and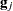 
is the gradient of 
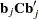with respect to 
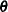, evaluated at 
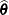. The matrix 
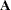is the asymptotic variance-covariance matrix of 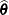, obtained from the second derivative matrix of the likelihood equations. You can display this matrix with the ASYCOV option in the PROC GLIMMIX statement.
Finally, let
 |
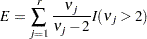where the indicator function eliminates terms for which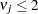 
. The degrees of freedom for 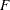are then computed as
 |
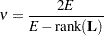provided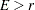 
; otherwise 
is set to zero.
In the one-dimensional case, when PROC GLIMMIX computes a test, the Satterthwaite degrees of freedom for the statistic
 |
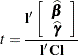are computed as
 |
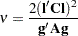where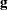 
is the gradient of 
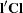with respect to 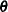, evaluated at .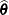