The GLIMMIX Procedure
-
Overview
-
Getting Started
-
Syntax
PROC GLIMMIX Statement BY Statement CLASS Statement CONTRAST Statement COVTEST Statement EFFECT Statement ESTIMATE Statement FREQ Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement NLOPTIONS Statement OUTPUT Statement PARMS Statement RANDOM Statement SLICE Statement STORE Statement WEIGHT Statement Programming Statements User-Defined Link or Variance Function
-
Details
Generalized Linear Models Theory Generalized Linear Mixed Models Theory GLM Mode or GLMM Mode Statistical Inference for Covariance Parameters Satterthwaite Degrees of Freedom Approximation Empirical Covariance (Sandwich) Estimators Exploring and Comparing Covariance Matrices Processing by Subjects Radial Smoothing Based on Mixed Models Odds and Odds Ratio Estimation Parameterization of Generalized Linear Mixed Models Response-Level Ordering and Referencing Comparing the GLIMMIX and MIXED Procedures Singly or Doubly Iterative Fitting Default Estimation Techniques Default Output Notes on Output Statistics ODS Table Names ODS Graphics
-
Examples
Binomial Counts in Randomized Blocks Mating Experiment with Crossed Random Effects Smoothing Disease Rates; Standardized Mortality Ratios Quasi-likelihood Estimation for Proportions with Unknown Distribution Joint Modeling of Binary and Count Data Radial Smoothing of Repeated Measures Data Isotonic Contrasts for Ordered Alternatives Adjusted Covariance Matrices of Fixed Effects Testing Equality of Covariance and Correlation Matrices Multiple Trends Correspond to Multiple Extrema in Profile Likelihoods Maximum Likelihood in Proportional Odds Model with Random Effects Fitting a Marginal (GEE-Type) Model Response Surface Comparisons with Multiplicity Adjustments Generalized Poisson Mixed Model for Overdispersed Count Data Comparing Multiple B-Splines Diallel Experiment with Multimember Random Effects Linear Inference Based on Summary Data
- References
| PROC GLIMMIX Contrasted with Other SAS Procedures |
The GLIMMIX procedure generalizes the MIXED and GENMOD procedures in two important ways. First, the response can have a nonnormal distribution. The MIXED procedure assumes that the response is normally (Gaussian) distributed. Second, the GLIMMIX procedure incorporates random effects in the model and so allows for subject-specific (conditional) and population-averaged (marginal) inference. The GENMOD procedure allows only for marginal inference.
The GLIMMIX and MIXED procedure are closely related; see the syntax and feature comparison in the section Comparing the GLIMMIX and MIXED Procedures. The remainder of this section compares the GLIMMIX procedure with the GENMOD, NLMIXED, LOGISTIC, and CATMOD procedures.
The GENMOD procedure fits generalized linear models for independent data by maximum likelihood. It can also handle correlated data through the marginal GEE approach of Liang and Zeger (1986) and Zeger and Liang (1986). The GEE implementation in the GENMOD procedure is a marginal method that does not incorporate random effects. The GEE estimation in the GENMOD procedure relies on R-side covariances only, and the unknown parameters in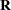 
are estimated by the method of moments. The GLIMMIX procedure allows G-side random effects and R-side covariances. PROC GLIMMIX can fit marginal (GEE-type) models, but the covariance parameters are not estimated by the method of moments. The parameters are estimated by likelihood-based techniques. When the GLIMMIX and GENMOD procedures fit a generalized linear model where the distribution contains a scale parameter, such as the normal, gamma, inverse gaussian, or negative binomial distribution, the scale parameter is reported in the "Parameter Estimates" table. For some distributions, the parameterization of this parameter differs. See the section Scale and Dispersion Parameters for details about how the GLIMMIX procedure parameterizes the log-likelihood functions and information about how the reported quantities differ between the two procedures.
Many of the fit statistics and tests in the GENMOD procedure are based on the likelihood. In a GLMM it is not always possible to derive the log likelihood of the data. Even if the log likelihood is tractable, it might be computationally infeasible. In some cases, the objective function must be constructed based on a substitute model. In other cases, only the first two moments of the marginal distribution can be approximated. Consequently, obtaining likelihood-based tests and statistics is difficult for many generalized linear mixed models. The GLIMMIX procedure relies heavily on linearization and Taylor-series techniques to construct Wald-type test statistics and confidence intervals. Likelihood ratio tests and confidence intervals for covariance parameters are available in the GLIMMIX procedure through the COVTEST statement.
The NLMIXED procedure fits nonlinear mixed models where the conditional mean function is a general nonlinear function. The class of generalized linear mixed models is a special case of the nonlinear mixed models; hence some of the models you can fit with PROC NLMIXED can also be fit with the GLIMMIX procedure. The NLMIXED procedure relies by default on approximating the marginal log likelihood through adaptive Gaussian quadrature. In the GLIMMIX procedure, maximum likelihood estimation by adaptive Gaussian quadrature is available with the METHOD=QUAD option in the PROC GLIMMIX statement. The default estimation methods thus differ between the NLMIXED and GLIMMIX procedures, because adaptive quadrature is possible for only a subset of the models available with the GLIMMIX procedure. If you choose METHOD=LAPLACE or METHOD=QUAD(QPOINTS=1) in the PROC GLIMMIX statement for a generalized linear mixed model, the GLIMMIX procedure performs maximum likelihood estimation based on a Laplace approximation of the marginal log likelihood. This is equivalent to the QPOINTS=1 option in the NLMIXED procedure.
The LOGISTIC and CATMOD procedures also fit generalized linear models; PROC LOGISTIC accommodates the independence case only. Binary, binomial, multinomial models for ordered data, and generalized logit models that can be fit with PROC LOGISTIC can also be fit with the GLIMMIX procedure. The diagnostic tools and capabilities specific to such data implemented in the LOGISTIC procedure go beyond the capabilities of the GLIMMIX procedure.