The GLIMMIX Procedure

Table 40.11 lists the statistics computed with the OUTPUT statement of the GLIMMIX procedure and their default names. This section provides further details about these statistics.

The distinction between prediction and confidence limits in Table 40.11 stems from the involvement of the predictors of the random effects. If the random-effect solutions (BLUPs, EBES) are involved, then the associated standard error used in computing the limits are standard errors of prediction rather than standard errors of estimation. The prediction limits are not limits for the prediction of a new observation.

The Pearson residuals in Table 40.11 are "Pearson-type" residuals, because the residuals are standardized by the square root of the marginal or conditional variance of an observation. Traditionally, Pearson residuals in generalized linear models are divided by the square root of the variance function. The GLIMMIX procedure divides by the square root of the variance so that marginal and conditional residuals have similar expressions. In other words, scale and overdispersion parameters are included.

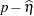When residuals or predicted values involve only the fixed effects part of the linear predictor (that is, ), then all model quantities are computed based on this predictor. For example, if the variance by which to standardize a marginal residual involves the variance function, then the variance function is also evaluated at the marginal mean, . 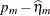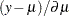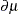Thus the residuals and can also be expressed as and , respectively, where is the derivative with respect to the linear predictor. To construct the residual 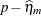in a GLMM, you can add the value of _ZGAMMA_ to the conditional residual 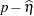. (The residual 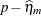is computed instead of the default marginal residual when you specify the CPSEUDO option in the OUTPUT statement.) If the predictor involves the BLUPs, then all relevant expressions and evaluations involve the conditional mean .

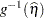The naming convention to add "PA" to quantities not involving the BLUPs is chosen to suggest the concept of a population average. When the link function is nonlinear, these are not truly population-averaged quantities, because 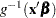does not equal 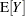in the presence of random effects. For example, if

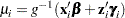is the conditional mean for subject 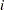, then

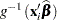does not estimate the average response in the population of subjects but the response of the average subject (the subject for which 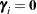). For models with identity link, the average response and the response of the average subject are identical.

The GLIMMIX procedure obtains standard errors on the scale of the mean by the delta method. If the link is a nonlinear function of the linear predictor, these standard errors are only approximate. For example,

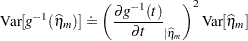Confidence limits on the scale of the data are usually computed by applying the inverse link function to the confidence limits on the linked scale. The resulting limits on the data scale have the same coverage probability as the limits on the linked scale, but they are possibly asymmetric.

In generalized logit models, confidence limits on the mean scale are based on symmetric limits about the predicted mean in a category. Suppose that the multinomial response in such a model has categories. The probability of a response in category 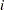is computed as

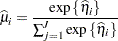The variance of 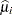is then approximated as

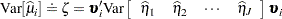where 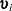is a 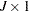vector with 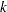th element

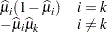The confidence limits in the generalized logit model are then obtained as

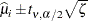where is the 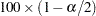percentile from a distribution with degrees of freedom. Confidence limits are truncated if they fall outside the 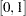interval.