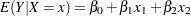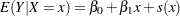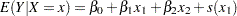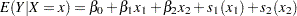PROC GAM: MODEL Statement :: SAS/STAT(R) 9.3 User's Guide

MODEL Statement

MODEL dependent <(options)> = <PARAM(effects)> <smoothing effects> </options> ;

MODEL event/trials = <PARAM(effects)> <smoothing effects> </options> ;

The MODEL statement specifies the dependent variable and the independent effects you want to use in the model. Specify the independent parametric variables inside the parentheses of PARAM( ). The parametric variables can be either classification variables or continuous variables. Classification variables must be declared in a CLASS statement. Interactions between variables can also be included as parametric effects. Multiple PARAM() statements are allowed in the MODEL statement. The syntax for the specification of effects is the same as for the GLM procedure ( Chapter 41, The GLM Procedure ).

Only continuous variables can be specified in smoothing effects. Any number of smoothing effects can be specified, as follows:

Smoothing Effect	Meaning
SPLINE(variable <, DF=number>)	Fit a smoothing spline with the variable and with DF=number
LOESS(variable <, DF=number>)	Fit a local regression with the variable and with DF=number
SPLINE2(variable1, variable2 <,DF=number>)	Fit a bivariate thin-plate smoothing spline with variable1 and variable2 and with DF=number

The number specified in the DF= option must be positive. If you specify neither the DF= option nor the METHOD=GCV in the MODEL statement, then the default used is DF=4. Note that for univariate spline and loess components, a degree of freedom is used by default to account for the linear portion of the model, so the value displayed in the “Fit Summary” and “Analysis of Deviance” tables will be one less than the value you specify.

Both parametric effects and smoothing effects are optional. If none are specified, a model that contains only an intercept is fitted.

If only parametric variables are present, PROC GAM fits a parametric linear model by using the terms inside the parentheses of PARAM( ). If only smoothing effects are present, PROC GAM fits a nonparametric additive model. If both types of effect are present, PROC GAM fits a semiparametric model by using the parametric effects as the linear part of the model.

Table 38.1 shows how to specify various models for a dependent variable y and independent variables x, x1, and x2. 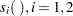$\text{[math]}$ are nonparametric smooth functions.

Table 38.1 Syntax for Common GAM Models
Type of Model	Syntax for `model`	Mathematical Form
Parametric	`y=param(x1 x2)`	$\text{[math]}$
Nonparametric	`y=spline(x)`	$\text{[math]}$
Nonparametric	`y=loess(x)`	$\text{[math]}$
Semiparametric	`y=spline(x1) param(x2)`	$\text{[math]}$
Additive	`y=spline(x1) spline(x2)`	$\text{[math]}$
Thin-plate spline	`y=spline2(x1,x2)`	$\text{[math]}$

Response Variable Options

Response variable options determine how the GAM procedure models probabilities for binary data.

You can specify the following options by enclosing them in parentheses after the response variable. See the section CLASS Statement for more detail.

DESCENDING

DESC

reverses the order of the response categories. If both the DESCENDING and ORDER= options are specified, PROC GAM orders the response categories according to the ORDER= option and then reverses that order.

EVENT=‘category’ $\text{[math]}$ | $\text{[math]}$ keyword

specifies the event category for the binary response model. PROC GAM models the probability of the event category. You can specify the value (formatted, if a format is applied) of the event category in quotes, or you can specify one of the following keywords. The default is EVENT=FIRST.

FIRST: designates the first ordered category as the event.
LAST: designates the last ordered category as the event.

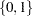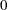One of the most common sets of response levels is $\text{[math]}$ , with $\text{[math]}$ representing the event for which the probability is to be modeled. Consider the example where Y takes the value $\text{[math]}$ and $\text{[math]}$ for event and nonevent, respectively, and X is the explanatory variable. By default, PROC GAM models the probability that Y 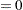$\text{[math]}$ . To model the probability that Y 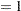$\text{[math]}$ , specify the following MODEL statement:

  model Y (event='1') = X;

ORDER=DATA | FORMATTED | FREQ | INTERNAL

specifies the sort order for the levels of the response variable. By default, ORDER=FORMATTED. When ORDER=FORMATTED, the values of numeric variables for which you have supplied no explicit format (that is, for which there is no corresponding FORMAT statement in the current PROC GAM run or in the DATA step that created the data set), are ordered by their internal (numeric) value. If you specify the ORDER= option in the MODEL statement and the ORDER= option in the CLASS statement, the former takes precedence. The following table shows the interpretation of the ORDER= values:

Value of ORDER=	Levels Sorted By
DATA	Order of appearance in the input data set
FORMATTED	External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal) value
FREQ	Descending frequency count; levels with the most observations come first in the order
INTERNAL	Unformatted value

For the FORMATTED and INTERNAL values, the sort order is machine-dependent.

For more information about sort order, see the chapter on the SORT procedure in the Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.

Model Options

ALPHA=number

specifies the significance level $\text{[math]}$ of the confidence limits on the final nonparametric component estimates when you request confidence limits to be included in the output data set. Specify number as a value between 0 and 1. The default value is 0.05. See the section OUTPUT Statement for more information about the OUTPUT statement.

ANODEV=type

specifies the type of method to be used to produce the "Analysis of Deviance" table for smoothing effects. The available choices are as follows:

REFIT: specifies that PROC GAM perform 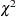$\text{[math]}$ tests by fitting nested GAM models. This is the default choice if you do not specify the ANODEV= option. This choice requires fitting separate GAM models where one smoothing term is omitted from each model.
NOREFIT: specifies that PROC GAM perform approximate tests of smoothing effects. To test each smoothing effect, a weighted least squares model is fitted to the remaining parametric part of the model while keeping other nonlinear smoothers fixed. For details, see Hastie (1991). This choice requires only a single GAM fitting to be performed, which reduces the time of the procedure.
NONE: requests that the procedure not produce the "Analysis of Deviance" table for smoothing effects.

DIST=distribution-id

LINK=distribution-id

specifies the distribution family used in the model. The choices for distribution-id are displayed in Table 38.2. See Distribution Family and Canonical Link for more information.

Table 38.2 Distribution Families for GAM Models
DIST=	Distribution	Link Function	Response Data Type
GAUSSIAN \| GAUS \| NORM	Normal (Gaussian)	Identity	Continuous variables
BINOMIAL \| LOGI \| BIN	Binomial	Logit	Binary variables
POISSON \| POIS \| LOGL	Poisson	Log	Nonnegative discrete variables
GAMMA \| GAMM	Gamma	Negative reciprocal	Positive continuous variables
IGAUSSIAN \| IGAU \| INVG	Inverse Gaussian	Squared reciprocal	Positive continuous variables

Canonical link functions are used with those distributions. Although alternative links are possible theoretically, the final fit of nonparametric regression models is relatively insensitive to the precise choice of link functions. Therefore, only the canonical link for each distribution family is implemented in PROC GAM. The loess smoother is not available for DIST=BINOMIAL when the number of trials is greater than 1.

EPSILON=number

specifies the convergence criterion for the backfitting algorithm. The default value is 1E $\text{[math]}$ .

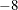EPSSCORE=number

specifies the convergence criterion for the local scoring algorithm. The default value is 1E $\text{[math]}$ .

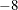ITPRINT

produces an iteration summary table for the smoothing effects when doing backfitting and local scoring.

MAXITER=number

specifies the maximum number of iterations for the backfitting algorithm. The default value is $\text{[math]}$ .

MAXITSCORE=number

specifies the maximum number of iterations for the local scoring algorithm. The default value is $\text{[math]}$ .

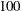METHOD=GCV

specifies that the value of the smoothing parameter should be selected by generalized cross validation. If you specify both METHOD=GCV and the DF= option for the smoothing effects, the user-specified DF is used, and the METHOD=GCV option is ignored. See the section Selection of Smoothing Parameters for more details on the GCV method.

OFFSET=variable

specifies an offset for the linear predictor. An offset plays the role of a predictor whose coefficient is known to be 1. For example, you can use an offset in a Poisson model when counts have been obtained in time intervals of different lengths. With a log link function, you can model the counts as Poisson variables with the logarithm of the time interval as the offset variable. The offset variable cannot appear in the CLASS statement or elsewhere in the MODEL statement.

The GAM Procedure

Response Variable Options

Model Options