The GAM Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Missing Values Nonparametric Regression Additive Models and Generalized Additive Models Forms of Additive Models Estimates from PROC GAM Backfitting and Local Scoring Algorithms Smoothers Selection of Smoothing Parameters Confidence Intervals for Smoothers Distribution Family and Canonical Link Dispersion Parameter Computational Resources ODS Table Names ODS Graphics
Missing Values Nonparametric Regression Additive Models and Generalized Additive Models Forms of Additive Models Estimates from PROC GAM Backfitting and Local Scoring Algorithms Smoothers Selection of Smoothing Parameters Confidence Intervals for Smoothers Distribution Family and Canonical Link Dispersion Parameter Computational Resources ODS Table Names ODS Graphics -
Examples

- References
Getting Started: GAM Procedure
The following example illustrates the use of the GAM procedure to explore in a nonparametric way how two factors affect a response. The data come from a study (Sockett et al. 1987) of the factors affecting patterns of insulin-dependent diabetes mellitus in children. The objective is to investigate the dependence of the level of serum C-peptide on various other factors in order to understand the patterns of residual insulin secretion. The response measurement is the logarithm of C-peptide concentration (pmol/ml) at diagnosis, and the predictor measurements are age and base deficit (a measure of acidity).
title 'Patterns of Diabetes';
data diabetes;
input Age BaseDeficit CPeptide @@;
logCP = log(CPeptide);
datalines;
5.2 -8.1 4.8 8.8 -16.1 4.1 10.5 -0.9 5.2
10.6 -7.8 5.5 10.4 -29.0 5.0 1.8 -19.2 3.4
12.7 -18.9 3.4 15.6 -10.6 4.9 5.8 -2.8 5.6
1.9 -25.0 3.7 2.2 -3.1 3.9 4.8 -7.8 4.5
7.9 -13.9 4.8 5.2 -4.5 4.9 0.9 -11.6 3.0
11.8 -2.1 4.6 7.9 -2.0 4.8 11.5 -9.0 5.5
10.6 -11.2 4.5 8.5 -0.2 5.3 11.1 -6.1 4.7
12.8 -1.0 6.6 11.3 -3.6 5.1 1.0 -8.2 3.9
14.5 -0.5 5.7 11.9 -2.0 5.1 8.1 -1.6 5.2
13.8 -11.9 3.7 15.5 -0.7 4.9 9.8 -1.2 4.8
11.0 -14.3 4.4 12.4 -0.8 5.2 11.1 -16.8 5.1
5.1 -5.1 4.6 4.8 -9.5 3.9 4.2 -17.0 5.1
6.9 -3.3 5.1 13.2 -0.7 6.0 9.9 -3.3 4.9
12.5 -13.6 4.1 13.2 -1.9 4.6 8.9 -10.0 4.9
10.8 -13.5 5.1
;
The following statements perform the desired analysis. The PROC GAM statement invokes the procedure and specifies the diabetes data set as input. The MODEL statement specifies logCP as the response variable and requests that univariate smoothing splines with the default of  degrees of freedom be used to model the effect of Age and BaseDeficit.
degrees of freedom be used to model the effect of Age and BaseDeficit.
ods graphics on;
proc gam data=diabetes;
model logCP = spline(Age) spline(BaseDeficit);
run;
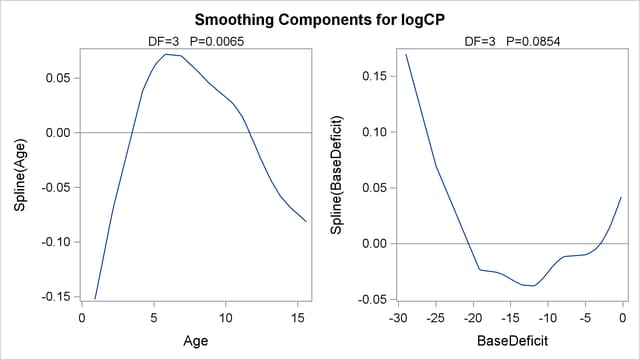
The results are shown in Figure 38.1 and Figure 38.2.
| Patterns of Diabetes |
| Summary of Input Data Set | |
|---|---|
| Number of Observations | 43 |
| Number of Missing Observations | 0 |
| Distribution | Gaussian |
| Link Function | Identity |
| Iteration Summary and Fit Statistics | |
|---|---|
| Final Number of Backfitting Iterations | 5 |
| Final Backfitting Criterion | 5.542745E-10 |
| The Deviance of the Final Estimate | 0.4180791724 |
Figure 38.1 shows two tables. The first table summarizes the input data set and the distributional family used for the model; the second table summarizes the convergence criterion for backfitting.
| Regression Model Analysis Parameter Estimates |
||||
|---|---|---|---|---|
| Parameter | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1.48141 | 0.05120 | 28.93 | <.0001 |
| Linear(Age) | 0.01437 | 0.00437 | 3.28 | 0.0024 |
| Linear(BaseDeficit) | 0.00807 | 0.00247 | 3.27 | 0.0025 |
| Smoothing Model Analysis Fit Summary for Smoothing Components |
||||
|---|---|---|---|---|
| Component | Smoothing Parameter |
DF | GCV | Num Unique Obs |
| Spline(Age) | 0.995582 | 3.000000 | 0.011675 | 37 |
| Spline(BaseDeficit) | 0.995299 | 3.000000 | 0.012437 | 39 |
| Smoothing Model Analysis Analysis of Deviance |
||||
|---|---|---|---|---|
| Source | DF | Sum of Squares | Chi-Square | Pr > ChiSq |
| Spline(Age) | 3.00000 | 0.150761 | 12.2605 | 0.0065 |
| Spline(BaseDeficit) | 3.00000 | 0.081273 | 6.6095 | 0.0854 |
Figure 38.2 displays summary statistics for the model. It consists of three tables. The first is the "Parameter Estimates" table for the parametric part of the model. It indicates that the linear trends for both Age and BaseDeficit are highly significant. The second table is the summary of smoothing components of the nonparametric part of the model. By default, each smoothing component has approximately 4 degrees of freedom (DF). For univariate spline components, one DF is taken up by the (parametric) linear part of the model, so the remaining approximate DF is 3, and the main point of this table is to present the smoothing parameter values that yield this DF for each component. Finally, the third table is the "Analysis of Deviance" table for the nonparametric component of the model.
Graphical displays are produced when ODS Graphics is enabled. By default, the graphics features of PROC GAM produce plots of the partial predictions of each variable. In these plots, the partial prediction for a predictor such as Age is its nonparametric contribution to the model, 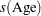 . For general information about ODS Graphics, see
Chapter 21,
Statistical Graphics Using ODS.
For specific information about the graphics available in the GAM procedure, see the section ODS Graphics.
. For general information about ODS Graphics, see
Chapter 21,
Statistical Graphics Using ODS.
For specific information about the graphics available in the GAM procedure, see the section ODS Graphics.
Plots for both predictors (Figure 38.3) show a strong quadratic pattern, with a possible indication of higher-order behavior. Further investigation is required to determine whether these patterns are real or not.