| The NLIN Procedure |
| Hougaard’s Measure of Skewness |
A "close-to-linear" nonlinear regression model, in the sense of Ratkowsky (1983, 1990), is a model in which parameter estimators have properties similar to those in a linear regression model. That is, the least-squares estimators of the parameters are close to being unbiased and normally distributed, and they have minimum variance.
A nonlinear regression model sometimes fails to be close to linear due to the properties of a single parameter. When this occurs, bias in the parameter estimates can render inferences that use the reported standard errors and confidence limits invalid. Ratkowsky (1990) notes that of the two curvature components in a nonlinear model—intrinsic curvature and parameter-effects curvature (Bates and Watts 1981)—the parameter-effects curvature is typically larger. It is this component that you can affect by changing the parameterization of a model. One motivation for fitting a nonlinear model in a different parameterization is to obtain a particular interpretation and to give parameter estimators more close-to-linear behavior. Example 60.4 shows how changing the parameterization of a four-parameter logistic model can reduce the parameter-effects curvature and can yield a useful parameter interpretation at the same time.
The degree to which a parameter estimator exhibits close-to-linear behavior can be assessed with Hougaard’s measure of skewness,  (Hougaard 1982, 1985). This measure is available through the HOUGAARD option in the PROC NLIN statement. Hougaard’s skewness measure for the
(Hougaard 1982, 1985). This measure is available through the HOUGAARD option in the PROC NLIN statement. Hougaard’s skewness measure for the 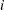 th parameter is defined as follows:
th parameter is defined as follows:
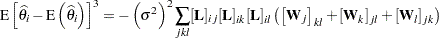 |
where the sum is a triple sum over the number of parameters and
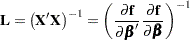 |
The term 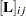 denotes the value in row
denotes the value in row 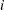 , column
, column 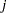 of the matrix
of the matrix 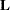 . (Hougaard (1985) uses superscript notation to denote elements in this inverse.) The matrix
. (Hougaard (1985) uses superscript notation to denote elements in this inverse.) The matrix 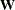 is a three-dimensional
is a three-dimensional 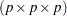 array
array
 |
 |
|||
 |
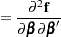 |
|||
 |
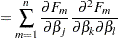 |
The third central moment is then normalized using the standard error as
 |
The previous expressions depend on the unknown values of the parameters and on the residual variance 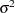 . In order to evaluate the Hougaard measure in a particular data set, the NLIN procedure computes
. In order to evaluate the Hougaard measure in a particular data set, the NLIN procedure computes
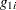 |
 |
|||
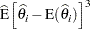 |
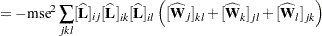 |
Following Ratkowsky (1990, p. 28), the following rules can be applied to the standardized Hougaard measure computed by the NLIN procedure:
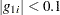
the estimator
 of parameter
of parameter 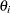 is very close to linear in behavior
is very close to linear in behavior 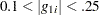
the estimator is reasonably close to linear
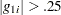
the skewness is very apparent

the nonlinear behavior is considerable
Copyright © SAS Institute, Inc. All Rights Reserved.