UDS stands for user defined sampler. The UDS statement allows you to use a separate algorithm, other than the default random walk Metropolis, to update parameters in the model. The purpose of the UDS statement is to give you a greater amount of flexibility and better control over the updating schemes of the Markov chain. Multiple UDS statements are allowed.

For the UDS statement to work properly, you have to do the following:

• write a subroutine by using PROC FCMP (see the FCMP Procedure in the Base SAS Procedures Guide) and save it to a SAS catalog (see the example in this section). The subroutine must update some parameters in the model. These are the UDS parameters. The subroutine is called the UDS subroutine.

• declare any UDS parameters in the PARMS statement with a sampling option, as in </ UDS> (see the section PARMS Statement).

• specify the prior distributions for all UDS parameters, using the PRIOR statements.

Note:All UDS parameters must appear in three places: the UDS statement, the PARMS statement, and the PRIOR statement. Otherwise, PROC MCMC exits.

To obtain a valid Markov chain, a UDS subroutine must update a parameter from its full posterior conditional distribution and not the posterior marginal distribution. The posterior conditional is something that you need to provide. This conditional is implicitly based on a prior distribution. PROC MCMC has no means to verify that the implied prior in the UDS subroutine is the same as the prior that you specified in the PRIOR statement. You need to make sure that the two distributions agree; otherwise, you will get misleading results.

The priors in the PRIOR statements do not directly affect the sampling of the UDS parameters. They could affect the sampling of the other parameters in the model, which, in turn, changes the behavior of the Markov chain. You can see this by noting cases where the hyperparameters of the UDS parameters are model parameters; the priors should be part of the posterior conditional distributions of these hyperparameters, and they cannot be omitted.

Some additional information is listed to help you better understand the UDS statement:

• Most features of the SAS programming language can be used in subroutines processed by PROC FCMP (see the FCMP Procedure in the Base SAS Procedures Guide).

• The UDS statement does not support FCMP functions—a FCMP function returns a value, while a subroutine does not. A subroutine updates some of its subroutine arguments. These arguments are called OUTARGS arguments.

• The UDS parameters cannot be in the same block as other parameters. The optional argument </ UDS> in the PARMS statement prevents parameters that use the default Metropolis from being mixed with those that are updated by the UDS subroutines.

• You can put all the UDS parameters in the same PARMS statement or have a separate UDS statement for each of them.

• The same subroutine can be used in multiple UDS statements. This feature comes in handy if you have a generic sampler that can be applied to different parameters.

• PROC MCMC updates the UDS parameters by calling the UDS subroutines directly. At every iteration, PROC MCMC first samples parameters that use the Metropolis algorithm, then the UDS parameters. Sampling of the UDS parameters proceeds in the order in which the UDS statements are listed.

• A UDS subroutine accepts any symbols in the program as well as any input data set variables as its arguments.

• Only the OUTARGS arguments in a UDS subroutine are updated in PROC MCMC. You can modify other arguments in the subroutine, but the changes are not global in the procedure.

• If a UDS subroutine has an argument that is a SAS data set variable, PROC MCMC steps through the data set while updating the UDS parameters. The subroutine is called once per observation in the data set for every iteration.

• If a UDS subroutine does not have any arguments that are data set variables, PROC MCMC does not access the data set while executing the subroutine. The subroutine is called once per iteration.

• To reduce the overhead in calling the UDS subroutine and accessing the data set repeatedly, you might consider reading all the input data set variables into arrays and using the arrays as the subroutine arguments. See the section BEGINCNST/ENDCNST Statement about how to use the BEGINCNST and ENDCNST statements to store data set variables.

An Example that Uses the UDS Statement

Suppose that you are interested in modeling normal data with conjugate prior distributions. The data are as follows:

title 'An Example that uses the UDS Statement';
 
data a;
   input y @@;
   i = _n_;
   datalines;
-0.651  17.435  -5.943  -2.543 -10.444
-5.754  -5.002  -2.545  -1.743   0.998
;

The likelihood for each observation is as follows:

The prior distributions on and 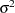are as follows:

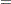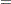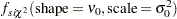where 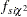is the density function for a scaled inverse chi-square distribution. To sample and 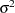without using any UDS statements, you can use the following program:

proc mcmc data=a seed=17;
   parm mu;
   parm s2;
   begincnst;
      mu0 = 0;  t0 = 20;
      nu0 = 10; s0 = 10;
   endcnst;
 
   prior mu ~ normal(mu0, var=t0);
   prior s2 ~ sichisq(nu0, s0);
   model y ~ normal(mu, var = s2);
run;

This is a case where the full posterior conditional distribution of given 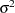and 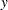has a closed form. It is also a normal distribution:

You can define a subroutine, muupdater, which generates a random normal sample from the posterior conditional distribution described previously.

proc fcmp outlib=sasuser.funcs.uds;
   subroutine muupdater(mu, s2, mu0, t0, n, sumy);
   outargs mu;
   sigma2 = 1 / (1/t0 + n/s2);
   mean = (mu0/t0 + sumy/s2) * sigma2;
   mu = rand("normal", mean, sqrt(sigma2));
   endsub;
run;

The subroutine is saved in the OUTLIB= library. The declaration of any subroutine begins with a SUBROUTINE statement and ends with an ENDSUB statement. The OUTARGS statement in the subroutine indicates that mu is updated. Others, such as sigma2, mu0, and so on, are arguments that are needed in the full conditional distribution. Here the rand and sqrt are two of the many SAS functions that you can use.

You specify a CMPLIB option to let SAS search each of the catalogs that are specified in the option for a package that contains muupdater.

options cmplib=sasuser.funcs;

To use the subroutine in the UDS statement, you can use the following statements:

proc mcmc data=a seed=17;
   UDS muupdater(mu, s2, mu0, t0, n, sumy);
   parm mu /uds;
   parm s2;
   begincnst;
      mu0 = 0;  t0 = 20;
      nu0 = 10; s0 = 10;
      n = 10;
      if i eq 1 then sumy = 0;
      sumy = sumy + y;
      call streaminit(1);
   endcnst;
 
   prior mu ~ normal(mu0, var=t0);
   prior s2 ~ sichisq(nu0, s0);
   model y ~ normal(mu, var = s2);
run;

These statements are very similar to the previous program. The differences are the UDS statement, the </ UDS> option in the PARMS statement, and a few lines that computes the values of sumy and n.

The symbol sumy is the sum of 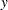. The value is obtained by taking advantage of the BEGINCNST and ENDCNST statements. See the example in the section BEGINCNST/ENDCNST Statement. The symbol n is the sample size in the data set.

The CALL STREAMINIT routine ensures that the RAND function in muupdater creates a reproducible stream of random numbers. The SEED= option specifies a seed for the random number generator in PROC MCMC, which does not control the random number generator in the RAND function in the subroutine. You need to set both to reproduce the same stream of Markov chain samples.

The two programs produce different but similar numbers (results not shown) for the posterior distributions of and .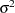

For a more realistic example that uses the UDS statement, see Implement a New Sampling Algorithm.