Example 88.4 Confirmatory Factor Analysis: Cognitive Abilities
In this example, cognitive abilities of 64 students from a middle school were measured. The fictitious data contain nine cognitive test scores. Three of the scores were for reading skills, three others were for math skills, and the remaining three were for writing skills. The covariance matrix for the nine variables was obtained. A confirmatory factor analysis with three factors was conducted. The following is the input data set and the PROC TCALIS specification for the analysis:
title "Confirmatory Factor Analysis Using the FACTOR Modeling Language";
title2 "Cognitive Data";
data cognitive1(type=cov);
_type_='cov';
input _name_ $ reading1 reading2 reading3 math1 math2 math3
writing1 writing2 writing3;
datalines;
reading1 83.024 . . . . . . . .
reading2 50.924 108.243 . . . . . . .
reading3 62.205 72.050 99.341 . . . . . .
math1 22.522 22.474 25.731 82.214 . . . . .
math2 14.157 22.487 18.334 64.423 96.125 . . . .
math3 22.252 20.645 23.214 49.287 58.177 88.625 . . .
writing1 33.433 42.474 41.731 25.318 14.254 27.370 90.734 . .
writing2 24.147 20.487 18.034 22.106 26.105 22.346 53.891 96.543 .
writing3 13.340 20.645 23.314 19.387 28.177 38.635 55.347 52.999 98.445
;
proc tcalis data=cognitive1 nobs=64 modification;
factor
Read_Factor -> reading1-reading3 = load1-load3,
Math_Factor -> math1-math3 = load4-load6,
Write_Factor -> writing1-writing3 = load7-load9;
pvar
Read_Factor Math_Factor Write_Factor = 3 * 1.,
reading1-reading3 math1-math3 writing1-writing3 = errvar1-errvar9;
run;
In the PROC TCALIS statement, the number of observations is specified with the NOBS= option. The MODIFICATION option in the same statement requests model modification indices be computed.
The FACTOR modeling language is the most handy tool for specifying confirmatory factor models. The FACTOR statement is used to invoke this modeling language. Entries in the FACTOR statement are for specifying factor-variables relationships and are separated by commas. In each entry, you first specify a latent factor, followed by the right arrow sign –>. Then you specify the observed variables that have nonzero loadings on the factor. Next, an equal sign is used to signify the specification of the loading parameters that follow. The loading parameters can be names (parameters without initial estimates), numbers (fixed values), or names followed by parenthesized numbers (parameter with initial values). In this example, there are three factors: Read_Factor, Math_Factor, and Write_Factor. These factors have simple cluster structures with the nine observed variables. Each observed variable has only one loading on exactly one factor, yielding a total of nine loading parameters named load1–load9. No initial estimates are specified for them. They are computed by PROC TCALIS.
In the PVAR statement, you specify the variances of the factors and the error variances for the observed variables. The factor variances in this model are fixed at ones for identification purposes. The error variances for the observed variables are free parameters without initial estimates, named errvar1–errvar9, respectively.
The covariances of the factors are not specified in the model, meaning that the factors are uncorrelated by default. Certainly, this might not be reasonable. But for illustration purposes, this uncorrelated factor model is fitted. With the MODIFICATION option in the PROC TCALIS statement, LM (Lagrange Multiplier) tests are conducted. The results of LM tests can suggest the inclusion of additional parameters for a better model fit. If the uncorrelated factor model is indeed unreasonable, it is shown in the results of the LM tests.
In Output 88.4.1, the initial model specification is echoed in matrix form. The observed variables and factors are also displayed.
Output 88.4.1
Uncorrelated Factor Model Specification
| reading1 reading2 reading3 math1 math2 math3 writing1 writing2 writing3 |
| Read_Factor Math_Factor Write_Factor |
| 1.0000 |
0 |
0 |
| 0 |
1.0000 |
0 |
| 0 |
0 |
1.0000 |
| errvar1 |
. |
| errvar2 |
. |
| errvar3 |
. |
| errvar4 |
. |
| errvar5 |
. |
| errvar6 |
. |
| errvar7 |
. |
| errvar8 |
. |
| errvar9 |
. |
In the table for initial factor loading matrix, the nine loading parameters are shown to have simple cluster relations with the factors. In the table for initial factor covariance matrix, the diagonal matrix shows that the factors are not correlated. The diagonal elements are fixed at ones so that this matrix is also a correlation matrix for the factors. In the table for initial error variances, the nine variance parameters are shown. No initial estimates were specified, as indicated by the missing values '.'.
In Output 88.4.2, initial estimates are generated by the instrumental variable method and the McDonald method.
Output 88.4.2
Optimization of the Uncorrelated Factor Model: Initial Estimates
| 1 |
Instrumental Variables Method |
| 2 |
McDonald Method |
| 7.15372 |
0.00851 |
| 7.80225 |
-0.00170 |
| 8.70856 |
-0.00602 |
| 7.68637 |
0.00272 |
| 8.01765 |
-0.01096 |
| 7.05012 |
0.00932 |
| 8.76776 |
-0.0009955 |
| 5.96161 |
-0.01335 |
| 7.23168 |
0.01665 |
| 31.84831 |
-0.00179 |
| 47.36790 |
0.0003461 |
| 23.50199 |
0.00257 |
| 23.13374 |
-0.0008384 |
| 31.84224 |
0.00280 |
| 38.92075 |
-0.00167 |
| 13.86035 |
-0.00579 |
| 61.00217 |
0.00115 |
| 46.14784 |
-0.00300 |
These initial estimates turn out to be pretty good, in the sense that only three more iterations are needed to converge to the maximum likelihood estimates and the final function value  does not change much from the initial function value
does not change much from the initial function value  , as shown in Output 88.4.3.
, as shown in Output 88.4.3.
Output 88.4.3
Optimization of the Uncorrelated Factor Model: Iteration Summary
| |
0 |
4 |
0 |
|
0.78792 |
0.1225 |
0.00175 |
0 |
0.932 |
| |
0 |
6 |
0 |
|
0.78373 |
0.00419 |
0.000037 |
0 |
1.051 |
| |
0 |
8 |
0 |
|
0.78373 |
5.087E-7 |
3.715E-9 |
0 |
1.001 |
| 3 |
11 |
| 5 |
0 |
| 0.783733415 |
3.7146571E-9 |
| 0 |
1.0006660673 |
| 0.0025042942 |
|
| Convergence criterion (ABSGCONV=0.00001) satisfied. |
The fit summary is shown in Output 88.4.4.
Output 88.4.4
Fit of the Uncorrelated Factor Model
| 64 |
| 9 |
| 45 |
| 18 |
| 0 |
| 272.0467 |
| 36 |
| 0.7837 |
| 49.3752 |
| 27 |
| 0.0054 |
| 2.5474 |
| 53 |
| 19.5739 |
| 0.2098 |
| 0.8555 |
| 0.7592 |
| 0.6416 |
| 0.1147 |
| 0.0617 |
| 0.1646 |
| 0.0271 |
| 1.4630 |
| 1.2069 |
| 1.8687 |
| -4.6248 |
| -89.9146 |
| -62.9146 |
| 0.8396 |
| 0.9052 |
| 0.8185 |
| 0.8736 |
| 0.7580 |
| 0.9087 |
| 0.6139 |
Using the chi-square model test criterion, the uncorrelated factor model should be rejected at  . The RMSEA estimate is
. The RMSEA estimate is  , which is not indicative of a good fit according to Browne and Cudeck (1993). Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen non-normed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only
, which is not indicative of a good fit according to Browne and Cudeck (1993). Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen non-normed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only  . It is thus safe to conclude that there could be some improvements on the model fit.
. It is thus safe to conclude that there could be some improvements on the model fit.
The MODIFICATION option in the PROC TCALIS statement has been used to request for computing the LM test indices for model modifications. The results are shown in Output 88.4.5.
Output 88.4.5
Lagrange Multiplier Tests
| 9.76596 |
0.0018 |
2.95010 |
| 3.58077 |
0.0585 |
1.89703 |
| 2.15312 |
0.1423 |
1.17976 |
| 1.87637 |
0.1707 |
1.41298 |
| 1.02954 |
0.3103 |
0.95427 |
| 0.91230 |
0.3395 |
0.99933 |
| 0.86221 |
0.3531 |
0.95672 |
| 0.63403 |
0.4259 |
0.73916 |
| 0.55602 |
0.4559 |
0.63906 |
| 0.55362 |
0.4568 |
0.74628 |
| 8.95268 |
0.0028 |
0.44165 |
| 7.07904 |
0.0078 |
0.40132 |
| 4.61896 |
0.0316 |
0.30411 |
| 5.45986 |
0.0195 |
-13.16822 |
| 5.05573 |
0.0245 |
12.32431 |
| 3.93014 |
0.0474 |
13.59149 |
| 2.83209 |
0.0924 |
-9.86342 |
| 2.56677 |
0.1091 |
10.15901 |
| 1.94879 |
0.1627 |
8.40273 |
| 1.75181 |
0.1856 |
-7.82777 |
| 1.57978 |
0.2088 |
-7.97915 |
| 1.34894 |
0.2455 |
7.77158 |
| 1.11704 |
0.2906 |
-7.23762 |
Three different tables for ranking the LM test results are shown. In the first table, the new loading parameters that would improve the model fit the most are shown first. For example, in the first row a new factor loading of writing1 on the Read_Factor is suggested to improve the model fit the most. The LM Stat value is 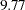 . This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of
. This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of 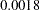 indicates a significant improvement of model fit at
indicates a significant improvement of model fit at  . Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
. Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
The other two tables in Output 88.4.5 shows the new parameters in factor covariances, error variances, or error covariances that would result in a better model fit. The table for the new parameters of the factor covariance matrix indicates that adding each of the covariances among factors might lead to a statistically significant improvement in model fit. This confirms with the initial argument that uncorrelated factors might not reasonable in this case—it fails to explain the covariances among observed variables through the correlations among latent factors. The largest LM Stat value in this table is  , which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit. To do this, you need to add the COV statement for specifying the covariances among factors to the original code. The following statements are used to specify the modified factor model with covariances among factors:
, which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit. To do this, you need to add the COV statement for specifying the covariances among factors to the original code. The following statements are used to specify the modified factor model with covariances among factors:
proc tcalis data=cognitive1 nobs=64;
factor
Read_Factor -> reading1-reading3 = load1-load3,
Math_Factor -> math1-math3 = load4-load6,
Write_Factor -> writing1-writing3 = load7-load9;
pvar
Read_Factor Math_Factor Write_Factor = 3 * 1.,
reading1-reading3 math1-math3 writing1-writing3 = errvar1-errvar9;
cov Read_Factor Math_Factor Write_Factor = fcov1-fcov3;
run;
The fit summary is shown in Output 88.4.6.
Output 88.4.6
Fit of the Correlated Factor Model
| 64 |
| 9 |
| 45 |
| 21 |
| 0 |
| 272.0467 |
| 36 |
| 0.4677 |
| 29.4667 |
| 24 |
| 0.2031 |
| 0.8320 |
| 79 |
| 5.7038 |
| 0.0607 |
| 0.9109 |
| 0.8330 |
| 0.6073 |
| 0.0601 |
| . |
| 0.1244 |
| 0.3814 |
| 1.2602 |
| . |
| 1.5637 |
| -18.5333 |
| -94.3465 |
| -70.3465 |
| 0.9582 |
| 0.9768 |
| 0.8917 |
| 0.9653 |
| 0.8375 |
| 0.9780 |
| 0.5945 |
The model fit chi-square value is  , which is about
, which is about 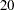 less than the model with uncorrelated factors. The
less than the model with uncorrelated factors. The  -value is
-value is  , indicating a fairly satisfactory model fit. The RMSEA value is
, indicating a fairly satisfactory model fit. The RMSEA value is  , which is close to
, which is close to 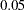 , a value recommended as an indication of good model fit by Browne and Cudeck (1993). More fit indices that do not attain the
, a value recommended as an indication of good model fit by Browne and Cudeck (1993). More fit indices that do not attain the  level with the uncorrelated factor model now have values close to or above
level with the uncorrelated factor model now have values close to or above  . These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet non-normed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
. These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet non-normed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
In Output 88.4.7, the estimation results for factor loadings are shown. All these loadings are statistically significant, indicating non-chance relationships with the factors.
Output 88.4.7
Estimation of the Factor Loading Matrix
| 6.7657 |
| 1.0459 |
| 6.4689 |
| [load1] |
|
|
|
| 7.8579 |
| 1.1890 |
| 6.6090 |
| [load2] |
|
|
|
| 9.1344 |
| 1.0712 |
| 8.5269 |
| [load3] |
|
|
|
|
| 7.5488 |
| 1.0128 |
| 7.4536 |
| [load4] |
|
|
|
| 8.4401 |
| 1.0838 |
| 7.7874 |
| [load5] |
|
|
|
| 6.8194 |
| 1.0910 |
| 6.2506 |
| [load6] |
|
|
|
|
| 7.9677 |
| 1.1254 |
| 7.0797 |
| [load7] |
|
|
|
| 6.8742 |
| 1.1986 |
| 5.7350 |
| [load8] |
|
|
|
| 7.0949 |
| 1.2057 |
| 5.8844 |
| [load9] |
|
In Output 88.4.8, the factor covariance matrix is shown. Because the diagonal elements are all ones, the off-diagonal elements are correlations among factors. The correlations range from  –
–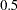 . These factors are moderately correlated.
. These factors are moderately correlated.
Output 88.4.8
Estimation of the Correlations of Factors
|
| 0.3272 |
| 0.1311 |
| 2.4955 |
| [fcov1] |
|
| 0.4810 |
| 0.1208 |
| 3.9813 |
| [fcov2] |
|
| 0.3272 |
| 0.1311 |
| 2.4955 |
| [fcov1] |
|
|
| 0.3992 |
| 0.1313 |
| 3.0417 |
| [fcov3] |
|
| 0.4810 |
| 0.1208 |
| 3.9813 |
| [fcov2] |
|
| 0.3992 |
| 0.1313 |
| 3.0417 |
| [fcov3] |
|
|
In Output 88.4.9, the error variances for variables are shown.
Output 88.4.9
Estimation of the Error Variances
| errvar1 |
37.24939 |
8.33997 |
4.46637 |
| errvar2 |
46.49695 |
10.69869 |
4.34604 |
| errvar3 |
15.90447 |
9.26097 |
1.71737 |
| errvar4 |
25.22889 |
7.72269 |
3.26685 |
| errvar5 |
24.89032 |
8.98327 |
2.77074 |
| errvar6 |
42.12110 |
9.20362 |
4.57658 |
| errvar7 |
27.24965 |
10.36489 |
2.62903 |
| errvar8 |
49.28881 |
11.39812 |
4.32429 |
| errvar9 |
48.10684 |
11.48868 |
4.18733 |
All  values except the one for reading3 are bigger than
values except the one for reading3 are bigger than 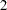 , a value close to a critical
, a value close to a critical  -value at
-value at  . This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this nonsignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
. This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this nonsignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
In addition to the parameter estimation results, PROC TCALIS also outputs supplementary results that could be useful for interpretations. In Output 88.4.10, the squared multiple correlations and the factor scores regression coefficients are shown.
Output 88.4.10
Supplementary Estimation Results
| 37.24939 |
83.02400 |
0.5513 |
| 46.49695 |
108.24300 |
0.5704 |
| 15.90447 |
99.34100 |
0.8399 |
| 25.22889 |
82.21400 |
0.6931 |
| 24.89032 |
96.12500 |
0.7411 |
| 42.12110 |
88.62500 |
0.5247 |
| 27.24965 |
90.73400 |
0.6997 |
| 49.28881 |
96.54300 |
0.4895 |
| 48.10684 |
98.44500 |
0.5113 |
| 0.02001 |
0.0006807 |
0.00198 |
| 0.01861 |
0.0006334 |
0.00185 |
| 0.06326 |
0.00215 |
0.00628 |
| 0.00112 |
0.04035 |
0.00281 |
| 0.00127 |
0.04572 |
0.00318 |
| 0.0006068 |
0.02183 |
0.00152 |
| 0.00319 |
0.00274 |
0.05128 |
| 0.00152 |
0.00131 |
0.02446 |
| 0.00161 |
0.00138 |
0.02587 |
The percentages of variance for the observed variables that can be explained by the factors are shown in the R-Square column of the table for squared multiple correlations (R-squares). These R-squares can be interpreted meaningfully because there is no reciprocal relationships among variables or correlated errors in the model. All estimates of R-squares are bounded between  and
and 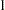 .
.
In the table for factor scores regression coefficients, entries are coefficients for the variables you can use to create the factor scores. The larger the coefficient, the more influence of the corresponding variable for creating the factor scores. It makes intuitive sense to see the cluster pattern of these coefficients—the reading measures are more important to create the latent variable scores of Read_Factor and so on.
 does not change much from the initial function value
does not change much from the initial function value  , as shown in Output 88.4.3.
, as shown in Output 88.4.3.  . The RMSEA estimate is
. The RMSEA estimate is  , which is not indicative of a good fit according to Browne and Cudeck (1993). Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen non-normed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only
, which is not indicative of a good fit according to Browne and Cudeck (1993). Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen non-normed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only  . It is thus safe to conclude that there could be some improvements on the model fit.
. It is thus safe to conclude that there could be some improvements on the model fit. 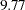 . This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of
. This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of 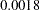 indicates a significant improvement of model fit at
indicates a significant improvement of model fit at  . Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
. Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.  , which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit. To do this, you need to add the COV statement for specifying the covariances among factors to the original code. The following statements are used to specify the modified factor model with covariances among factors:
, which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit. To do this, you need to add the COV statement for specifying the covariances among factors to the original code. The following statements are used to specify the modified factor model with covariances among factors:  , which is about
, which is about 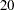 less than the model with uncorrelated factors. The
less than the model with uncorrelated factors. The  -value is
-value is  , indicating a fairly satisfactory model fit. The RMSEA value is
, indicating a fairly satisfactory model fit. The RMSEA value is  , which is close to
, which is close to 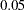 , a value recommended as an indication of good model fit by Browne and Cudeck (1993). More fit indices that do not attain the
, a value recommended as an indication of good model fit by Browne and Cudeck (1993). More fit indices that do not attain the  level with the uncorrelated factor model now have values close to or above
level with the uncorrelated factor model now have values close to or above  . These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet non-normed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
. These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet non-normed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.  –
–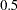 . These factors are moderately correlated.
. These factors are moderately correlated.  values except the one for reading3 are bigger than
values except the one for reading3 are bigger than 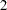 , a value close to a critical
, a value close to a critical  -value at
-value at  . This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this nonsignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
. This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this nonsignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.  and
and 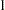 .
.