Example 88.5 Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis

You can use PROC TCALIS to do multiple-group or multiple-sample analysis. The groups in the analysis must be independent. In this example, a relatively simple multiple-group analysis is carried out. The covariance matrices of two independent groups are tested for equality. Hence, individual covariance matrices are actually not structured. Rather, they are constrained to be the same under the null hypothesis. See Example 88.10 for a more sophisticated example of multiple-group analysis.

In this example, a reaction time experiment was conducted on two groups of individuals. One group () was considered to be an expert group with prior training related to the tasks of the experiment. Another group (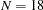) was a control group without prior training. Three tasks of dexterity were administered to all individuals. These tasks differed by their required complexity levels of body skills. They were labeled as high, medium, and low complexities.

Apparently, the differential performance of the two groups under different task complexities was the primary research objective. In this example, however, you are interested in testing whether the groups have the same covariance matrix for the tasks. Equality of covariance matrices might be an essential assumption in some statistical tests for comparing group means. In this example, you will use PROC TCALIS to see the tenability of such an assumption. The covariance matrices for the two groups are stored in the data sets Expert and Novice, as shown in the following:

   data expert(type=cov);
      input _type_ $ _name_ $ high medium low;
      datalines;
   COV   high    5.88     .      .
   COV   medium  2.88    7.16    .
   COV   low     3.12    4.44   8.14
   ;
   
   data novice(type=cov);
      input _type_ $ _name_ $ high medium low;
      datalines;
   COV   high    6.42     .      .
   COV   medium  1.24    8.25    .
   COV   low     4.26    2.75   7.99
   ;

These data sets are read into the analysis through the GROUP statements in the following PROC TCALIS specification:

   proc tcalis;
      group 1 / data=expert nobs=20 label="Expert";
      group 2 / data=novice nobs=18 label="Novice";
      model 1 / groups=1,2;
         mstruct 
            var=high medium low;
            matrix _COV_ [1,1] = v_high v_medium v_low,
                         [2,]  = cov21,
                         [3,]  = cov31 cov32;
      fitindex NoIndexType On(only)=[chisq df probchi] 
               chicorrect=eqcovmat;
      ods select ModelingInfo MSTRUCTVariables MSTRUCTCovInit Fit;
   run;

The first GROUP statement defines group 1 for the expert group. The second GROUP statement defines group 2 for the novice group. The NOBS= option is used in both statements to provide the number of observations of these groups. The LABEL= option is used in these statements to provide meaningful group labels.

The MODEL statement defines MODEL 1. In the analysis, this model fits both groups 1 and 2, as indicated by the GROUPS= option of the statement. An MSTRUCT model for MODEL 1 is defined immediately afterward. Three variables, high, medium, and low, are specified in the VAR= option of the MSTRUCT statement. These three variables are also the row and column variables in the _COV_ matrix defined in the MATRIX statement.

In the first entry of the MATRIX statement, the diagonal elements of the _COV_ matrix are specified. Starting with the element [1,1] (and implicitly followed by [2,2] and [3,3]), variances for the three variables are parameters named v_high, v_medium, and v_low, respectively. In the second entry of the MATRIX statement, parameter specification starts with (and also ends with) the first element of the second row (that is, [2,1]) of the _COV_ matrix. The covariance between the variables high and medium is specified as cov21. In the last entry of the MATRIX statement, parameter specification starts with the first element of the third row (that is, [3,1] and then [3,2]) of the _COV_ matrix. The covariance between the variables high and low is specified as cov31 and the covariance between the variables medium and low is specified as cov32. No initial values are provided in this example. PROC TCALIS generates initial values by some reasonable methods.

There are six parameters in the covariance matrix _COV_, which also has six nonredundant elements in its general form as a symmetric matrix. Hence, model 1 is saturated. If this model were to fit a single group, it would have indicated a perfect model fit with zero chi-square value. Such a model is quite trivial and not of interest. But with two independent groups being fitted by this single model, it becomes a nontrivial model in which you test the equality of the two covariance matrices. Having this main purpose in mind, you use options in the FITINDEX statement to extract the relevant results that could answer your question. First, you use the NOINDEXTYPE option to suppress the printing of the index types in the fit summary table. Then, you use the ON(ONLY)= option to specify the fit indices printed in the fit summary table. In this example, only the model fit chi-square statistic, degrees of freedom, and the probability value of the test are requested. Finally, you use the CHICORRECT=EQCOVMAT option to request a chi-square correction for the test of equality of covariance matrices. This correction is due to Box (1949) and is implemented in PROC TCALIS as a built-in chi-square correction option.

In addition, because you are not interested in all displayed output, you use the ODS SELECT statement to display only those output (or ODS tables) of interest. In this example, only the modeling information, the variables involved, the initial covariance matrix specification, and the fit summary table are printed. All output in PROC TCALIS are named as an ODS table. To locate a particular output in PROC TCALIS, you must know the corresponding ODS table names. See the section ODS Table Names for a listing of ODS table names used by PROC TCALIS.

Output 88.5.1 displays some information regarding the basic model setup.

The modeling information table summarizes some basic information about the two groups. Both of them are fitted by model 1. The next table shows the variables involved: high, medium, and low. The order of variables in this table is the same as that of the row and column variables of the covariance model matrix, which is shown next. The parameters for the entries in the covariance matrix are shown. The names of parameters are displayed in parentheses. No initial estimates are given as input, as indicated by the missing value '.'.

The fit summary table is shown in Output 88.5.2, which has been much simplified for the current example due to the uses of some options in the FITINDEX statement.

As shown in Output 88.5.2, the chi-square test statistic is 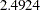. With six degrees of freedom, the test statistic is not significant at 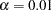. Therefore, the fitted model is supported, which means that the equality of the covariance matrices of the groups is tenable.