| The TCALIS Procedure |
| FACTOR Statement |
- FACTOR <EFA_options | CFA_spec> ;
where EFA_options are exploratory factor analysis options, CFA_spec is confirmatory factor analysis specification defined as:
factor-variables-relation < , factor-variables-relation > ...
and each factor-variables-relation is defined as:
factor –> variables = parameter-spec
In the FACTOR statement, you can specify either EFA_options, CFA_spec, or neither of these. However, you cannot specify both EFA_options and CFA_spec at the same time.
If an EFA_option (exploratory factor analysis option) is specified immediately after the FACTOR statement, or neither EFA_options nor factor-variable-relations are specified in the FACTOR statement, an exploratory factor model is analyzed. Otherwise, specifying an CFA_spec (confirmatory factor analysis specification) invokes a confirmatory factor model. These two types of models are discussed in the next two sections.
Exploratory Factor Analysis
For the exploratory factor model with orthogonal factors, PROC TCALIS assumes the following model structures for the population covariance or correlation matrix 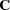 :
:
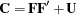 |
where 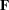 is the factor loading matrix and
is the factor loading matrix and  is a diagonal matrix of error variances. In this section,
is a diagonal matrix of error variances. In this section,  denotes the number of manifest variables corresponding to the rows and columns of matrix
denotes the number of manifest variables corresponding to the rows and columns of matrix 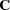 , and
, and  denotes the number of factors (or components, if the COMPONENT option is specified in the FACTOR statement) corresponding to the columns of the factor loading matrix
denotes the number of factors (or components, if the COMPONENT option is specified in the FACTOR statement) corresponding to the columns of the factor loading matrix 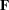 . While the number of manifest variables is set automatically by the number of variables in the VAR statement or in the input data set, the number of factors can be set by the N= option in the FACTOR statement.
. While the number of manifest variables is set automatically by the number of variables in the VAR statement or in the input data set, the number of factors can be set by the N= option in the FACTOR statement.
The unrestricted exploratory factor model is not identified because any orthogonal rotated factor loading matrix 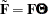 satisfies the same model structures as
satisfies the same model structures as 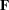 does, where
does, where 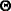 is any orthogonal matrix so that
is any orthogonal matrix so that 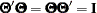 . Mathematically, the covariance or correlation structures can be expressed as:
. Mathematically, the covariance or correlation structures can be expressed as:
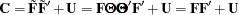 |
To obtain an identified orthogonal factor solution as a starting point, the 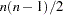 elements in the upper triangle of
elements in the upper triangle of 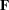 are constrained to zeros in PROC TCALIS. Initial estimates for factor loadings and unique variances are computed by an algebraic method of approximate factor analysis. Given the initial estimates, final estimates are obtained through the iterative optimization of an objective function, which depends on the estimation method specified in the METHOD= option (default with ML—maximum likelihood) of the PROC TCALIS statement.
are constrained to zeros in PROC TCALIS. Initial estimates for factor loadings and unique variances are computed by an algebraic method of approximate factor analysis. Given the initial estimates, final estimates are obtained through the iterative optimization of an objective function, which depends on the estimation method specified in the METHOD= option (default with ML—maximum likelihood) of the PROC TCALIS statement.
To make the factor solution more interpretable, you can use the ROTATE= option in the FACTOR statement to obtain a rotated factor loading matrix with a "simple" pattern. Rotation can be orthogonal or oblique. The rotated factors remain uncorrelated after an orthogonal rotation but would be correlated after an oblique rotation. The model structures of an oblique solution are expressed in the following equation:
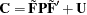 |
where 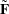 is the rotated factor loading matrix and
is the rotated factor loading matrix and 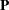 is a symmetric matrix for factor correlations. See the sections The FACTOR Model and Exploratory Factor Analysis Models for more details about exploratory factor models.
is a symmetric matrix for factor correlations. See the sections The FACTOR Model and Exploratory Factor Analysis Models for more details about exploratory factor models.
You can also do exploratory factor analysis by the more dedicated FACTOR procedure. Even though extensive comparisons of the factor analysis capabilities between the FACTOR and TCALIS procedures are not attempted here, some general points can be made here. In general, the FACTOR procedure provides more factor analysis options than the TCALIS procedure does, although both procedures have some unique factor analysis features that are not shared by the other. PROC TCALIS requires more computing time and memory than PROC FACTOR because it is designed for more general structural estimation problems and is not able to exploit all the special properties of the unconstrained factor analysis model. For maximum likelihood analysis, you can use either PROC FACTOR (with METHOD=ML, which is not the default method in PROC FACTOR) or PROC TCALIS. Because the initial unrotated factor solution obtained by PROC FACTOR uses a different set of identification constraints than that of PROC TCALIS, you would observe different initial ML factor solutions for the procedures. Nonetheless, the initial solutions by both procedures are statistically equivalent.
The following exploratory factor analysis options are available in the FACTOR statement.
- COMPONENT | COMP
computes a component analysis instead of a factor analysis (the diagonal matrix
 in the model is set to 0). Note that the rank of
in the model is set to 0). Note that the rank of 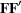 is equal to the number
is equal to the number  of components in
of components in 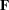 . If
. If  is smaller than the number of variables in the moment matrix
is smaller than the number of variables in the moment matrix 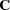 , the matrix of predicted model values is singular and maximum likelihood estimates for
, the matrix of predicted model values is singular and maximum likelihood estimates for 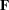 cannot be computed. You should compute ULS estimates in this case.
cannot be computed. You should compute ULS estimates in this case. - HEYWOOD | HEY
constrains the diagonal elements of
 to be nonnegative. Equivalently, you can constrain these elements to positive values by the BOUNDS statement.
to be nonnegative. Equivalently, you can constrain these elements to positive values by the BOUNDS statement. - GAMMA=p
specifies the orthomax weight used with the option ROTATE=ORTHOMAX. Alternatively, you can use ROTATE=ORTHOMAX(p) with p representing the orthomax weight. There is no restriction on valid values for the orthomax weight, although the most common values are between 0 and the number of variables. The default GAMMA= value is one, resulting in the varimax rotation.
- N=n
specifies the number of first-order factors or components. The number of factors (
 ) should not exceed the number of manifest variables (
) should not exceed the number of manifest variables ( ) in the analysis. For the saturated model with
) in the analysis. For the saturated model with 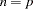 , the COMP option should generally be specified for
, the COMP option should generally be specified for 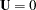 ; otherwise,
; otherwise, 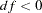 . For
. For 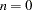 no factor loadings are estimated, and the model is
no factor loadings are estimated, and the model is 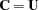 , with
, with 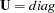 . By default,
. By default, 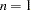 .
. - NORM<= KAISER | NONE>
Kaiser-normalizes the rows of the factor pattern for rotation. NORM=KAISER, which is the default, has exactly the same effect as NORM. You can turn off the normalization by NORM=NONE.
- RCONVERGE=p
- RCONV=p
specifies the convergence criterion for rotation cycles. Rotation stops when the scaled change of the simplicity function value is less than the RCONVERGE= value. The default convergence criterion is:
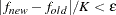
where
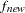 and
and 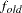 are simplicity function values of the current cycle and the previous cycle, respectively,
are simplicity function values of the current cycle and the previous cycle, respectively, 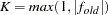 is a scaling factor, and
is a scaling factor, and  is 1E–9 by default and is modified by the RCONVERGE= value.
is 1E–9 by default and is modified by the RCONVERGE= value. - RITER=i
specifies the maximum number of cycles
 for factor rotation. The default
for factor rotation. The default  is the greater of 10 times the number of variables and 100.
is the greater of 10 times the number of variables and 100. - ROTATE | R=name
specifies an orthogonal or oblique rotation of the initial factor solution. Although ROTATE=PRINCIPAL is actually not a rotation method, it is put here for convenience. By default, ROTATE=NONE.
Valid names for orthogonal rotations are as follows:
- BIQUARTIMAX | BIQMAX
specifies orthogonal biquartimax rotation. This corresponds to the specification ROTATE=ORTHOMAX(0.5).
- EQUAMAX | E
specifies orthogonal equamax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=
 /2.
/2. - FACTORPARSIMAX | FPA
specifies orthogonal factor parsimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=n.
- NONE | N
specifies that no rotation be performed, leaving the original orthogonal solution.
- ORTHCF(p1,p2) | ORCF(p1,p2)
specifies the orthogonal Crawford-Ferguson rotation (Crawford and Ferguson 1970) with the weights p1 and p2 for variable parsimony and factor parsimony, respectively. See the definitions of weights in Chapter 33, The FACTOR Procedure.
- ORTHGENCF(p1,p2,p3,p4) | ORGENCF(p1,p2,p3,p4)
specifies the orthogonal generalized Crawford-Ferguson rotation (Jennrich 1973), with the four weights p1, p2, p3, and p4. For the definitions of these weights, see the section Simplicity Functions for Rotations in Chapter 33, The FACTOR Procedure.
- ORTHOMAX<(p1)> | ORMAX<(p1)>
specifies the orthomax rotation (see Harman 1976) with orthomax weight p1. If ROTATE=ORTHOMAX is used, the default p1 value is 1 unless specified otherwise in the GAMMA= option. Alternatively, ROTATE=ORTHOMAX(p1) specifies p1 as the orthomax weight or the GAMMA= value. For the definitions of the orthomax weight, see the section Simplicity Functions for Rotations in Chapter 33, The FACTOR Procedure.
- PARSIMAX | PA
specifies orthogonal parsimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with
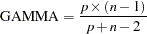
- PRINCIPAL | PC
specifies a principal axis rotation. If ROTATE=PRINCIPAL is used with a factor rather than a component model, the following rotation is performed:
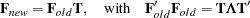
where the columns of matrix
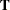 contain the eigenvectors of
contain the eigenvectors of 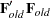 .
. - QUARTIMAX | QMAX | Q
specifies orthogonal quartimax rotation. This corresponds to the specification ROTATE=ORTHOMAX(0).
- VARIMAX | V
specifies orthogonal varimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=1.
Valid names for oblique rotations are as follows:
- BIQUARTIMIN | BIQMIN
specifies biquartimin rotation. It corresponds to the specification ROTATE=OBLIMIN(.5) or ROTATE=OBLIMIN with TAU=.5.
- COVARIMIN | CVMIN
specifies covarimin rotation. It corresponds to the specification ROTATE=OBLIMIN(1) or ROTATE=OBLIMIN with TAU=1.
- OBBIQUARTIMAX | OBIQMAX
- OBEQUAMAX | OE
- OBFACTORPARSIMAX | OFPA
- OBLICF(p1,p2) | OBCF(p1,p2)
specifies the oblique Crawford-Ferguson rotation (Crawford and Ferguson 1970) with the weights p1 and p2 for variable parsimony and factor parsimony, respectively. For the definitions of these weights, see the section Simplicity Functions for Rotations in Chapter 33, The FACTOR Procedure.
- OBLIGENCF(p1,p2,p3,p4) | OBGENCF(p1,p2,p3,p4)
specifies the oblique generalized Crawford-Ferguson rotation (Jennrich 1973) with the four weights p1, p2, p3, and p4. For the definitions of these weights, see the section Simplicity Functions for Rotations in Chapter 33, The FACTOR Procedure.
- OBLIMIN<(p1)> | OBMIN<(p1)>
specifies the oblimin rotation with oblimin weight p1. If ROTATE=OBLIMIN is used, the default p1 value is zero unless specified otherwise in the TAU= option. Alternatively, ROTATE=OBLIMIN(p1) specifies p1 as the oblimin weight or the TAU= value. For the definitions of the oblimin weight, see the section Simplicity Functions for Rotations in Chapter 33, The FACTOR Procedure.
- OBPARSIMAX | OPA
- OBQUARTIMAX | OQMAX
specifies oblique quartimax rotation. This is the same as the QUARTIMIN method.
- OBVARIMAX | OV
- QUARTIMIN | QMIN
specifies quartimin rotation. It is the same as the oblique quartimax method. It also corresponds to the specification ROTATE=OBLIMIN(0) or ROTATE=OBLIMIN with TAU=0.
- TAU=p
specifies the oblimin weight used with the option ROTATE=OBLIMIN. Alternatively, you can use ROTATE=OBLIMIN(p) with p representing the oblimin weight. There is no restriction on valid values for the oblimin weight, although for practical purposes a negative or zero value is recommended. The default TAU= value is 0, resulting in the quartimin rotation.
Confirmatory Factor Analysis
- FACTOR factor-variable-relations ;
- PVAR partial variance parameters ;
- COV covariance parameters ;
- MEAN mean parameters ;
If you specify at least one factor-variable-relation, a confirmatory factor analysis is assumed. Whenever applicable, you can use the PVAR, COV, and MEAN statements to specify the variance, partial variance, covariance, and mean parameters. The model structures for the covariance matrix 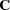 of the confirmatory factor model are described in the following equation:
of the confirmatory factor model are described in the following equation:
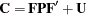 |
where 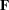 is the factor loading matrix,
is the factor loading matrix, 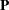 is a symmetric matrix for factor correlations, and
is a symmetric matrix for factor correlations, and  is a diagonal matrix of error variances.
is a diagonal matrix of error variances.
If the mean structures are also analyzed, the model structures for the mean vector 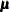 of the confirmatory factor model are described in the following equation:
of the confirmatory factor model are described in the following equation:
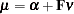 |
where  is the intercept vector for the observed variables and
is the intercept vector for the observed variables and 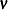 is the vector for factor means. See the sections The FACTOR Model and Confirmatory Factor-Analysis Models for more details about confirmatory factor models.
is the vector for factor means. See the sections The FACTOR Model and Confirmatory Factor-Analysis Models for more details about confirmatory factor models.
You can use the PVAR statement to specify factor variance parameters in the diagonal of matrix 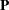 , or the error variances in the diagonal of matrix
, or the error variances in the diagonal of matrix  . These variances, by default, are automatically added as free parameters in the factor model even if you do not specify them. However, if you want to set constraints on these parameters, it is useful to define them explicitly by using the PVAR statement. For example, you might like to set some variances to fixed constants, or you might want to set equality constraints by using the same parameter name at different parameter locations in your model.
. These variances, by default, are automatically added as free parameters in the factor model even if you do not specify them. However, if you want to set constraints on these parameters, it is useful to define them explicitly by using the PVAR statement. For example, you might like to set some variances to fixed constants, or you might want to set equality constraints by using the same parameter name at different parameter locations in your model.
You can use the COV statement to specify factor covariance parameters. These factor covariances are the off-diagonal elements of matrix 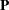 . Unlike the factor variances, factor covariances are assumed to be fixed zeros by default. Note that you cannot use the COV statement to specify the error covariances—they are always fixed zeros in the confirmatory factor-analysis model.
. Unlike the factor variances, factor covariances are assumed to be fixed zeros by default. Note that you cannot use the COV statement to specify the error covariances—they are always fixed zeros in the confirmatory factor-analysis model.
You can use the MEAN statement to specify the means of the factors in vector 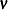 and the intercepts of the manifest variables in vector
and the intercepts of the manifest variables in vector  . All the factor means and intercepts are fixed zeros if you do not specify them explicitly.
. All the factor means and intercepts are fixed zeros if you do not specify them explicitly.
Suppose that you want to fit a factor model with nine manifest variables V1-V9. In this factor model, you assume a general factor and three group-factors, with three variables defining each group-factor. The following FACTOR statement shows the specification of such a model:
factor
g_factor -> V1-V9 (9 * g_load__),
factor_a -> V1-V3 (3 * load_a__),
factor_b -> V4-V6 (3 * load_b__),
factor_c -> V7-V9 (3 * load_c__);
In this example, you are fitting a factor matrix of the following form:
g_factor factor_a factor_b factor_c
V1 g_load1 load_a1
V2 g_load2 load_a2
V3 g_load3 load_a3
V4 g_load4 load_b1
V5 g_load5 load_b2
V6 g_load6 load_b3
V7 g_load7 load_c1
V8 g_load8 load_c2
V9 g_load9 load_c3
The blanks in the factor matrix denotes fixed zeros. Because you do not specify the covariances by using the COV statement, g_factor, factor_a, factor_b, and factor_c are all uncorrelated in the model.
Modifying a FACTOR Model from a Reference Model
In this section, it is assumed that you use a REFMODEL statement within the scope of a MODEL statement and the reference model (or base model) is a factor model, either exploratory or confirmatory. The reference model is referred to as the old model, while the model makes reference to this old model is referred to as the new model. If the new model is not intended to be an exact copy of the old FACTOR model, you can use the following extended FACTOR modeling language to make modifications from the old model before transferring the specifications to the new model.
Before discussing the syntax for modifying factor models, there are two cases where using the REFMODEL statement for defining new factor models are not recommended. First, if your old model is an exploratory factor-analysis model, then specification by using the FACTOR modeling language in the new model will replace the old model completely. In this case, the use of the REFMODEL statement is superfluous and should be avoided. Second, if your old model is a confirmatory factor-analysis model, then specification of an exploratory factor model by using the FACTOR statement in the new model will also replace the old model completely. Again, in this case the use of the REFMODEL statement is superfluous and should be avoided.
The nontrivial case where you might find the REFMODEL statement useful is when you modify an old confirmatory factor model to form a new confirmatory factor model. This nontrivial case is the focus of discussion in the remaining of the section.
The extended FACTOR modeling language for modifying model specification bears the same syntax as that of the ordinary FACTOR modeling language (see the section Confirmatory Factor Analysis). The syntax is:
- FACTOR factor-variable-relation ;
- PVAR partial variance parameters ;
- COV covariance parameters ;
- MEAN mean parameters ;
The new model is formed by integrating with the old model in the following ways:
- Duplication:
If you do not specify in the new model a parameter location that exists in the old model, the old parameter specification is duplicated in the new model.
- Addition:
If you specify in the new model a parameter location that does not exist in the old model, the new parameter specification is added in the new model.
- Deletion:
If you specify in the new model a parameter location that also exists in the old model and the new parameter is denoted by the missing value '.', the old parameter specification is not copied into the new model.
- Replacement:
If you specify in the new model a parameter location that also exists in the old model and the new parameter is not denoted by the missing value '.', the new parameter specification replaces the old one in the new model.
For example, consider the following two-group analysis:
proc tcalis;
group 1 / data=d1;
group 2 / data=d2;
model 1 / group=1;
factor
F1 -> V1-V3 = 1. load1 load2,
F2 -> V4-V6 = 1. load3 load4,
F3 -> V7-V9 = 1. load5 load6;
cov
F1 F2 = c12,
F2 F3 = c23;
pvar
F1-F3 = c1-c3,
V1-V9 = ev1-ev9;
model 2 / group=2;
refmodel 1;
factor
F1 -> V1 = loada,
F2 -> V4 = loadb,
F3 -> V7 = loadc;
cov
F1 F2 = .,
F1 F3 = c13;
run;
In this specification, you specify model 2 by referring to model 1 in the REFMODEL statement; model 2 is the new model which refers to the old model, model 1. Because the PVAR statement is not used in new model, all variance and partial variance parameter specifications in the PVAR statement of the old model are duplicated in the new model. The covariance parameter c23 for covariance between F2 and F3 in the COV statement of the old model is also duplicated in the new model. Similarly, loading parameters load1–load6 for some specific factor matrix locations are duplicated from the old model to the new model.
In the new model, there is an additional parameter specification that does not exist in the old model. In the COV statement of the new model, covariance parameter c13 for the covariance between F1 and F3 is added.
In the same statement, the covariance between F1 and F2 is denoted by the missing value '.'. This means that this parameter location in the old model should not be included in the new model. The consequence of this deletion from the old model is that the covariance between F1 and F2 is a fixed zero in the new model.
Finally, the three new loading specifications in the FACTOR statement of the new model replaces the fixed ones in the old model. They are now free parameters loada, loadb, and loadc in the new model.
Note: This procedure is experimental.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.