| The TCALIS Procedure |
| The FACTOR Model |
The FACTOR modeling language is used for specifying exploratory and confirmatory factor-analysis models. You can use other general modeling languages such as LINEQS, LISMOD, PATH, and RAM to specify a factor model. But the FACTOR modeling language is more convenient for specifying factor models and is more specialized in outputting factor-analytic results. For convenience, models specified by the FACTOR modeling language are called FACTOR models.
Types of Variables in the FACTOR Model
Each variable in the FACTOR model is either manifest or latent. Manifest variables are those variables that are measured in the research. They must be present in the input data set. Latent variables are not measured. Each latent variable in the FACTOR model can either be a factor or an error term.
Factors are unmeasured hypothetical constructs for explaining the covariances among manifest variables, while errors are the unique parts of the manifest variables that are not explained by the (common) factors.
In the FACTOR model, all manifest variables are endogenous, which means that they are predicted from the latent variables. In contrast, all latent variables in the FACTOR model are exogenous, which means that they serve as predictors only.
Naming Variables in the FACTOR Model
Manifest variables in the FACTOR model are referenced in the input data set. In the FACTOR model specification, you use their names as they appear in the input data set. Manifest variable names must not be longer than 32 characters. There are no further restrictions on these names beyond those required by the SAS system.
Error variables in the FACTOR model are not named explicitly, although they are assumed in the model. You can name latent factors only in confirmatory FACTOR models. Factor names must not be longer than 32 characters and must be distinguishable from the manifest variable names in the same analysis. You do not need to name factors in exploratory FACTOR models, however. Latent factors named Factor1, Factor2, and so on are generated automatically in exploratory FACTOR models.
Model Matrices in the FACTOR Model
Suppose in the FACTOR model that there are  manifest variables and
manifest variables and  factors. The FACTOR model matrices are summarized as follows:
factors. The FACTOR model matrices are summarized as follows:
Matrix 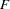 (
(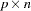 ) : Factor Loading Matrix
) : Factor Loading Matrix
The rows of 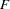 represent the
represent the  manifest variables, while the columns represent the
manifest variables, while the columns represent the  factors. Each row of
factors. Each row of 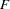 contains the factor loadings of a variable on all factors in the model.
contains the factor loadings of a variable on all factors in the model.
Matrix  (
(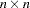 ) : Factor Covariance Matrix
) : Factor Covariance Matrix
The  matrix is a symmetric matrix for the variances of and covariances among the
matrix is a symmetric matrix for the variances of and covariances among the  factors.
factors.
Matrix 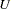 (
(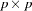 ) : Error Covariance Matrix
) : Error Covariance Matrix
The 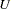 matrix represents an
matrix represents an 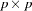 diagonal matrix for the error variances for the manifest variables. Elements in this matrix are the parts of variances of the manifest variables that are not explained by the common factors. Note that all off-diagonal elements of
diagonal matrix for the error variances for the manifest variables. Elements in this matrix are the parts of variances of the manifest variables that are not explained by the common factors. Note that all off-diagonal elements of 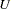 are fixed zeros in the FACTOR model.
are fixed zeros in the FACTOR model.
Vector  (
(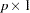 ) : Intercepts
) : Intercepts
If the mean structures are analyzed, vector  represents the intercepts of the manifest variables.
represents the intercepts of the manifest variables.
Vector  (
(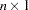 ) : Factor Means
) : Factor Means
If the mean structures are analyzed, vector  represents the means of the factors.
represents the means of the factors.
Matrix Representation of the FACTOR Model
Let  be a
be a 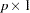 vector of manifest variables,
vector of manifest variables,  be an
be an 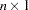 vector of latent factors, and
vector of latent factors, and  be a
be a 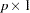 vector of errors. The factor model is written as:
vector of errors. The factor model is written as:
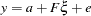 |
With the model matrix definitions in the previous section, the covariance matrix 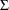 (
(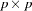 ) of manifest variables is structured as:
) of manifest variables is structured as:
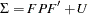 |
The mean vector 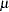 (
(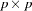 ) of manifest variables is structured as:
) of manifest variables is structured as:
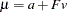 |
Exploratory Factor Analysis Models
So far confirmatory and exploratory models are not distinguished in deriving the covariance and mean structures. These two types of models are now distinguished in terms of the required structures or restrictions in model matrices.
Traditionally, exploratory factor analysis is applied when the relationships of manifest variables with factors have not been well-established in research. All manifest variables are allowed to have nonzero loadings on the factors in the model. First, factors are extracted and an initial solution is obtained. Then, for ease of interpretation a final factor solution is usually derived by rotating the factor space. Factor-variable relationships are determined by interpreting the final factor solution. This is different from the confirmatory factor analysis in which the factor-variable relationships are prescribed and to be confirmed.
Nonetheless, in terms of initial model fitting, exploratory factor analysis is not different from confirmatory factor analysis. In PROC TCALIS, the initial exploratory factor solution is obtained from a specific confirmatory factor model with restricted model matrices, which are described as follows:
The factor loading matrix
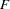 has
has 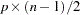 fixed zeros at the upper triangle portion of the matrix.
fixed zeros at the upper triangle portion of the matrix. The factor covariance matrix
 is an identity matrix, which means that factors are not correlated.
is an identity matrix, which means that factors are not correlated. The error covariance matrix
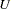 is a diagonal matrix.
is a diagonal matrix. The mean structures are not modeled. That is, no specification in
 or
or  vector is allowed.
vector is allowed.
For example, for an analysis with nine variables and three factors, the relevant model matrices of an exploratory FACTOR model have the following patterns:
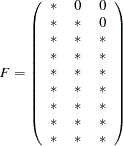 |
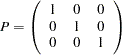 |
and
 |
where * denotes free parameters in the model matrices.
It is emphasized that most of these patterns are put on the initial factor solutions only. If an initial factor solution is rotated afterward, only the pattern of the error covariance matrix 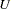 remains unchanged. That is, it is still a diagonal matrix after rotation. In general, rotating a factor solution will eliminate the fixed zero pattern in the upper triangle of the factor loading matrix
remains unchanged. That is, it is still a diagonal matrix after rotation. In general, rotating a factor solution will eliminate the fixed zero pattern in the upper triangle of the factor loading matrix 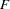 . If you apply an orthogonal rotation, the factor covariance matrix
. If you apply an orthogonal rotation, the factor covariance matrix  will not change. It is an identity matrix before and after rotation. However, if you apply an oblique rotation, in general the rotated factor covariance matrix
will not change. It is an identity matrix before and after rotation. However, if you apply an oblique rotation, in general the rotated factor covariance matrix  will not be an identity matrix and the off-diagonal elements will not be zeros.
will not be an identity matrix and the off-diagonal elements will not be zeros.
Confirmatory Factor-Analysis Models
In confirmatory FACTOR models, there are no imposed patterns on the 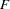 ,
,  ,
,  , and
, and  model matrices. All elements in these model matrices can be specified. However, for model identification, you might need to specify some factor loadings or factor variances as constants.
model matrices. All elements in these model matrices can be specified. However, for model identification, you might need to specify some factor loadings or factor variances as constants.
The only model restriction in confirmatory FACTOR models is placed on 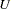 , which must be a diagonal matrix, as in exploratory FACTOR models too.
, which must be a diagonal matrix, as in exploratory FACTOR models too.
For example, for a confirmatory factor analysis with nine variables and three factors, you might specify the following patterns for the model matrices:
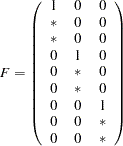 |
 |
and
 |
where * denotes free parameters in the model matrices.
In this confirmatory factor model, mean structures are not modeled. In addition, there are some distinctive features that underscore the differences between confirmatory and exploratory models:
Factor loading matrix
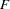 contains mostly zero elements and few nonzero free parameters, a pattern which is seen in most confirmatory factor models. In contrast, in exploratory factor models most elements in the
contains mostly zero elements and few nonzero free parameters, a pattern which is seen in most confirmatory factor models. In contrast, in exploratory factor models most elements in the 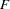 matrix are nonzero parameters.
matrix are nonzero parameters. Factor loading matrix
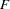 contains fixed values of ones. These fixed values are used for model identification purposes (that is, identifying the scales of the latent variables). In general, you always have to make sure that your confirmatory factor models are identified by putting fixed values in appropriate parameter locations in the model matrices. However, this is not a concern in exploratory FACTOR models because identification has been ensured by imposing certain patterns on the model matrices.
contains fixed values of ones. These fixed values are used for model identification purposes (that is, identifying the scales of the latent variables). In general, you always have to make sure that your confirmatory factor models are identified by putting fixed values in appropriate parameter locations in the model matrices. However, this is not a concern in exploratory FACTOR models because identification has been ensured by imposing certain patterns on the model matrices. The nonzero off-diagonal parameters in the factor covariance matrix
 indicate that correlated factors are hypothesized in the confirmatory factor model. This cannot be the case with the initial model of exploratory FACTOR models, where the
indicate that correlated factors are hypothesized in the confirmatory factor model. This cannot be the case with the initial model of exploratory FACTOR models, where the  matrix must be an identity matrix before rotation.
matrix must be an identity matrix before rotation.
Summary of Matrices in the FACTOR Model
Let  be the number of manifest variables and
be the number of manifest variables and  be the number of factors in the FACTOR model. The names, roles, and dimensions of the FACTOR model matrices are shown in the following table:
be the number of factors in the FACTOR model. The names, roles, and dimensions of the FACTOR model matrices are shown in the following table:
Matrix |
Name |
Description |
Dimensions |
|---|---|---|---|
|
_FACTLOAD_ |
factor loading matrix |
|
|
_FACTFCOR_ |
factor covariance matrix |
|
|
_FACTERRV_ |
error covariance matrix |
|
|
_FACTINTE_ |
intercepts |
|
|
_FACTMEAN_ |
factor means |
|
Specification of the Exploratory Factor Model
Because all initial model matrices of exploratory FACTOR models are predefined in PROC TCALIS, you do not need to specify any other parameters in the model matrices. To obtain desired factor solutions, you can use various options for exploratory factor analysis in the FACTOR statement. These options are the EFA_options in the FACTOR statement. Two main types of EFA_options are shown as follows:
options for factor extraction: COMPONENT, HEYWOOD, N=.
options for factor rotation: GAMMA=, NORM=, RCONVERGE=, RITER=, ROTATE=, TAU=.
For example, the following statement requests that three factors are extracted, followed by a varimax rotation of the initial factor solution:
factor n=3 rotate=varimax;
See the FACTOR statement for details about the EFA_options.
Specification of the Confirmatory Factor Model
To specify a confirmatory FACTOR model, you specify the factor-variable relationships in the FACTOR statement, the factor variances and error variances in the PVAR statement, the factor covariances in the COV statement, and the means and intercepts in the MEAN statement.
Specification of Factor-Variable Relationships
The CFA_spec in the FACTOR statement is for specifying the factor-variables relationships. For example, in the following statement you specify three factors F1, F2, and F3 that are related to different clusters of observed variables V1–V9:
factor
F1 -> V1-V3 = 1. parm1 (.4) parm2 (.4),
F2 -> V4-V6 = 1. parm3 parm4,
F3 -> V7-V9 = 1. parm5 parm6 (.3);
In the specification, variable V1 has a fixed loading of 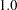 on F1. Variables V2 and V3 have loadings on F1 also. These two loadings are free parameters named parm1 and parm2, respectively. Initial estimates can be set in parentheses after the free parameters. For example, both parm1 and parm2 have initial values at
on F1. Variables V2 and V3 have loadings on F1 also. These two loadings are free parameters named parm1 and parm2, respectively. Initial estimates can be set in parentheses after the free parameters. For example, both parm1 and parm2 have initial values at 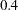 . Similarly, relationships of factor F2 with V4–V6, and of factor F3 with V7–V9 are defined in the same FACTOR statement. Providing initial estimates for parameters is optional. In this example, parm3, parm4, and parm5 are all free parameters without initial values provided. PROC TCALIS can determine appropriate initial estimates for these parameters. See the descriptions about CFA_spec in the FACTOR statement for more details about the syntax.
. Similarly, relationships of factor F2 with V4–V6, and of factor F3 with V7–V9 are defined in the same FACTOR statement. Providing initial estimates for parameters is optional. In this example, parm3, parm4, and parm5 are all free parameters without initial values provided. PROC TCALIS can determine appropriate initial estimates for these parameters. See the descriptions about CFA_spec in the FACTOR statement for more details about the syntax.
Specification of Factor Variances and Error Variances
You can specify the factor variances and error variances in the PVAR statement. For example, consider the following statement:
pvar F1-F3 = fvar1-fvar3,
V1-V9 = evar1-evar9 (9*10.);
In the PVAR statement, you specify the variances of factors F1, F2, and F3 as free parameters fvar1, fvar2, and fvar3, respectively; and the error variances for manifest variables V1–V9 as free parameters evar1–evar9, respectively. Each of the error variance parameters is given a starting value at 10. See the PVAR statement on for more details about the syntax.
Specification of Factor Covariances
You can specify the factor covariances in the COV statement. For example, you specify the covariances among factors F1, F2, and F3 in the following statement:
cov F1 F2 = cov12,
F1 F3 = cov13,
F2 F3 = cov23;
The covariance parameters are named cov12, cov13, and cov23, respectively. They represent the lower triangular elements of the factor covariance matrix  . See the COV statement on for more details about the syntax.
. See the COV statement on for more details about the syntax.
Specification of Means and Intercepts
If mean structures are of interest, you can also specify the factor means and the intercepts for the manifest variables in the MEAN statement. For example, consider the following statement:
mean F1-F3 = fmean1-fmean3,
V1-V9 = 9*12.;
In this statement, you specify the factor means of F1, F2, and F3 as free parameters fmean1, fmean2, and fmean3, respectively; and the intercepts for variables V1–V9 as fixed parameters at 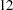 . See the MEAN statement on for more details about the syntax.
. See the MEAN statement on for more details about the syntax.
Default Parameters in the FACTOR Model
In the initial exploratory FACTOR model, all fixed and free parameters of the model are prescribed or set by default. These prescribed or default parameters include a fixed pattern for the factor loading matrix 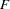 , a diagonal pattern for the error variance matrix
, a diagonal pattern for the error variance matrix 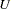 , and an identity matrix for factor covariance matrix
, and an identity matrix for factor covariance matrix  . See the section Exploratory Factor Analysis Models for more details about the patterns of the exploratory FACTOR model.
. See the section Exploratory Factor Analysis Models for more details about the patterns of the exploratory FACTOR model.
In the confirmatory FACTOR model, the error covariance matrix 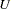 is restricted to be a diagonal matrix. In other words, covariances of errors are restricted to zeros. Other than that, you can specify any other parameter locations in the all model matrices. These includes all the parameter locations in the factor loading matrix
is restricted to be a diagonal matrix. In other words, covariances of errors are restricted to zeros. Other than that, you can specify any other parameter locations in the all model matrices. These includes all the parameter locations in the factor loading matrix 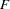 , the factor covariance matrix
, the factor covariance matrix  , the diagonal of the error covariance matrix
, the diagonal of the error covariance matrix 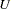 , the factor mean vector
, the factor mean vector  , and the intercept vector
, and the intercept vector  . If any of these parameter locations are not specified, default parameters are applied. There are two types of default parameters: one is automatic free parameter, and the other is fixed zero.
. If any of these parameter locations are not specified, default parameters are applied. There are two types of default parameters: one is automatic free parameter, and the other is fixed zero.
Automatic Free Parameters
The set of automatic free parameters in the confirmatory FACTOR model are:
the variances of factors; that is, the diagonal elements of the factor covariance matrix

the error variances for the manifest variables; that is, the diagonal elements of the error covariance matrix
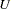
Each automatic free parameter is named with prefix _Add and appended with a unique integer. The reason for automatic parameter generation is to safeguard a proper FACTOR model specification. See the section Rationale of the Default Parameters in the LINEQS Model for a more detailed explanation.
Default Fixed Zeros
All unspecified parameter locations that are neither model-imposed specifications nor automatic free parameters in the confirmatory FACTOR model matrices are fixed zeros by default.
Note: This procedure is experimental.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.