| The TCALIS Procedure |
| The RAM Model |
The RAM modeling language is adapted from the basic RAM model developed by McArdle (1980). For brevity, models specified by the RAM modeling language are called RAM models, although it is noted that you can also specify these so-called RAM models by other general modeling languages supported in PROC TCALIS.
Types of Variables in the RAM Model
A variable in the RAM model is manifest if it is observed and is defined in the input data set. A variable in the RAM model is latent if it is not manifest. Because error variables are not explicitly named in the RAM model, all latent variables in the RAM model are considered as factors (non-error-type latent variables).
A variable in the RAM model is endogenous if it ever serves as an outcome variable in the RAM model. That is, an endogenous variable has at least one path (or an effect) from another variable in the model. A variable is exogenous if it is not endogenous. Endogenous variables are also referred to as dependent variables, while exogenous variables are also referred to as independent variables.
In the RAM model, exogenous/endogenous and latent/manifest distinctions for variables are not essential to the definitions of model matrices, although they are useful for conceptual understanding when the model matrices are partitioned.
Naming Variables in the RAM Model
Manifest variables in the RAM model are referenced in the input data set. Their names must not be longer than 32 characters. There is no further restrictions beyond those required by the SAS system.
Latent variables in the RAM model are those not being referenced in the input data set. Their names must not be longer than 32 characters. Unlike the LINEQS model, you do not need to use any specific prefix (for example, 'F' or 'f') for the latent factor names. The reason is that error or disturbance variables in the RAM model are not named explicitly in the RAM model. Thus, any variable names that are not referenced in the input data set are for latent factors.
As a general naming convention, you should not use Intercept as either a manifest or latent variable name.
Model Matrices in the RAM Model
In terms of the number of model matrices involved, the RAM model is the simplest among all the general structural equations models supported by PROC TCALIS. Essentially, there are only three model matrices in the RAM model: one for the interrelationships among variables, one for the variances and covariances, and one for the means and intercepts. These matrices are discussed in the following.
Matrix  (
(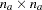 ) : Effects of Column Variables on Row Variables
) : Effects of Column Variables on Row Variables
The row and column variables of matrix  are the set of manifest and latent variables in the RAM model. Unlike the LINEQS model, the set of latent variables in the RAM model matrix does not include the error or disturbance variables. Each entry or element in the
are the set of manifest and latent variables in the RAM model. Unlike the LINEQS model, the set of latent variables in the RAM model matrix does not include the error or disturbance variables. Each entry or element in the  matrix represents an effect of the associated column variable on the associated row variable or a path coefficient from the associated column variable to the associated row variable. A zero entry means an absence of a path or an effect.
matrix represents an effect of the associated column variable on the associated row variable or a path coefficient from the associated column variable to the associated row variable. A zero entry means an absence of a path or an effect.
The pattern of matrix  determines whether a variable is endogenous or exogenous. A variable in the RAM model is endogenous if its associated row in the
determines whether a variable is endogenous or exogenous. A variable in the RAM model is endogenous if its associated row in the  matrix has at least one nonzero entry. Any other variable in the RAM model is exogenous.
matrix has at least one nonzero entry. Any other variable in the RAM model is exogenous.
Mathematically, you do not need to arrange the set of variables for matrix  in a particular order, as long as the order of variables is the same for the rows and the columns. However, arranging the variables according to whether they are endogenous or exogenous is useful to show the partitions of the model matrices and certain mathematical properties. See the section Partitions of the RAM Model Matrices and Some Restrictions for details.
in a particular order, as long as the order of variables is the same for the rows and the columns. However, arranging the variables according to whether they are endogenous or exogenous is useful to show the partitions of the model matrices and certain mathematical properties. See the section Partitions of the RAM Model Matrices and Some Restrictions for details.
Matrix  (
(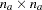 ): Variances, Covariances, Partial Variances, and Partial Covariances
): Variances, Covariances, Partial Variances, and Partial Covariances
The row and column variables of matrix  refer to the same set of manifest and latent variables defined in the RAM model matrix
refer to the same set of manifest and latent variables defined in the RAM model matrix  . The diagonal entries of
. The diagonal entries of  contain variances or partial variances of variables. If a variable is exogenous, then the corresponding diagonal element in the
contain variances or partial variances of variables. If a variable is exogenous, then the corresponding diagonal element in the  matrix represents its variance. Otherwise, the corresponding diagonal element in the
matrix represents its variance. Otherwise, the corresponding diagonal element in the  matrix represents its partial variance. This partial variance is an unsystematic source of variance not explained by the interrelationships of variables in the model. In most cases, you can interpret a partial variance as the error variance for an endogenous variable.
matrix represents its partial variance. This partial variance is an unsystematic source of variance not explained by the interrelationships of variables in the model. In most cases, you can interpret a partial variance as the error variance for an endogenous variable.
The off-diagonal elements of  contain covariances or partial covariances among variables. An off-diagonal element in
contain covariances or partial covariances among variables. An off-diagonal element in  associated with exogenous row and column variables represents covariance between the two exogenous variables. An off-diagonal element in
associated with exogenous row and column variables represents covariance between the two exogenous variables. An off-diagonal element in  associated with endogenous row and column variables represents partial covariance between the two variables. This partial covariance is unsystematic, in the sense that it is not explained by the interrelationships of variables in the model. In most cases, you can interpret a partial covariance as the error covariance between the two endogenous variables involved. An off-diagonal element in
associated with endogenous row and column variables represents partial covariance between the two variables. This partial covariance is unsystematic, in the sense that it is not explained by the interrelationships of variables in the model. In most cases, you can interpret a partial covariance as the error covariance between the two endogenous variables involved. An off-diagonal element in  associated with one exogenous variable and one endogenous variable in the row and column represents the covariance between the exogenous variable and the error of the endogenous variable. While this interpretation sounds a little awkward and inelegant, this kind of covariance, fortunately, is rare in most applications.
associated with one exogenous variable and one endogenous variable in the row and column represents the covariance between the exogenous variable and the error of the endogenous variable. While this interpretation sounds a little awkward and inelegant, this kind of covariance, fortunately, is rare in most applications.
Vector 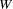 (
(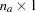 ): Intercepts and Means
): Intercepts and Means
The row variables of vector 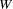 refer to the same set of manifest and latent variables defined in the RAM model matrix
refer to the same set of manifest and latent variables defined in the RAM model matrix  . Elements in
. Elements in 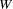 represent either intercepts or means. An element in
represent either intercepts or means. An element in 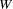 associated with an exogenous row variable represents the mean of the variable. An element in
associated with an exogenous row variable represents the mean of the variable. An element in 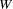 associated with an endogenous row variable represents the intercept term for the variable.
associated with an endogenous row variable represents the intercept term for the variable.
Covariance and Mean Structures
Assuming that 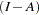 is invertible, where
is invertible, where  is the identity matrix of the same dimension as
is the identity matrix of the same dimension as  , the structured covariance matrix of all variables (including latent variables) in the RAM model is shown as follows:
, the structured covariance matrix of all variables (including latent variables) in the RAM model is shown as follows:
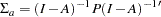 |
The structured mean vector of all variables is shown as follows:
 |
The covariance and mean structures of all manifest variables are obtained by selecting the elements in 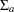 and
and 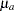 . This can be achieved by defining a selection matrix
. This can be achieved by defining a selection matrix 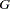 of dimensions
of dimensions 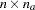 , where
, where  is the number of manifest variables in the model. The selection matrix
is the number of manifest variables in the model. The selection matrix 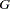 contains zeros and ones as its elements. Each row of
contains zeros and ones as its elements. Each row of 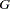 has exactly one nonzero element at the position that corresponds to the location of a manifest row variable in
has exactly one nonzero element at the position that corresponds to the location of a manifest row variable in 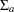 or
or 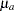 . With each row of
. With each row of 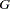 selecting a distinct manifest variable, the structured covariance matrix of all manifest variables is expressed as the following:
selecting a distinct manifest variable, the structured covariance matrix of all manifest variables is expressed as the following:
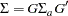 |
The structured mean vector of all observed variables is expressed as the following:
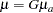 |
Partitions of the RAM Model Matrices and Some Restrictions
There are some model restrictions in the RAM model matrices. Although these restrictions do not affect the derivation of the covariance and mean structures, they are enforced in the RAM model specification.
For convenience, it is useful to assume that 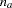 variables are arranged in the order of
variables are arranged in the order of 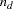 endogenous (or dependent) variables and the
endogenous (or dependent) variables and the 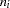 exogenous (independent) variables in the rows and columns of the model matrices.
exogenous (independent) variables in the rows and columns of the model matrices.
Model Restrictions on the  Matrix
Matrix
The  matrix is partitioned as:
matrix is partitioned as:
 |
where 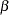 is an
is an 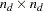 matrix for paths or effects from (column) endogenous variables to (row) endogenous variables and
matrix for paths or effects from (column) endogenous variables to (row) endogenous variables and 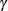 is an
is an 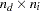 matrix for paths or effects from (column) exogenous variables to (row) endogenous variables.
matrix for paths or effects from (column) exogenous variables to (row) endogenous variables.
As shown in the matrix partitions, there are four submatrices. The two at the lower parts are seemingly structured to zeros. However, this should not be interpreted as restrictions imposed by the model. The zero submatrices are artifacts created by the exogenous-endogenous arrangement of the row and column variables. The only restriction on the  matrix is that the diagonal elements must all be zeros. This implies that the diagonal elements of the submatrix
matrix is that the diagonal elements must all be zeros. This implies that the diagonal elements of the submatrix 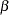 are also zeros. This restriction prevents a direct path from any endogenous variable to itself. There are no restrictions on the pattern of
are also zeros. This restriction prevents a direct path from any endogenous variable to itself. There are no restrictions on the pattern of 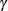 .
.
Partition of the  Matrix
Matrix
The  matrix is partitioned as:
matrix is partitioned as:
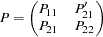 |
where 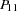 is an
is an 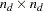 partial covariance matrix for the endogenous variables,
partial covariance matrix for the endogenous variables,  is an
is an 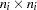 covariance matrix for the exogenous variables, and
covariance matrix for the exogenous variables, and  is an
is an 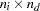 covariance matrix between the exogenous variables and the error terms for the endogenous variables. Because
covariance matrix between the exogenous variables and the error terms for the endogenous variables. Because  is symmetric,
is symmetric, 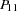 and
and  are also symmetric.
are also symmetric.
There are virtually no model restrictions placed on these submatrices. However, in most statistical application, errors for endogenous variables represent unsystematic sources of effects and therefore they are not to be correlated with other systematic sources such as the exogenous variables in the RAM model. This means that in most practical applications  would be a null matrix, although this is not enforced in PROC TCALIS.
would be a null matrix, although this is not enforced in PROC TCALIS.
Partition of the 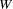 Vector
Vector
The 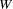 vector is partitioned as:
vector is partitioned as:
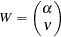 |
where  is an
is an  vector for intercepts of the endogenous variables and
vector for intercepts of the endogenous variables and  is an
is an 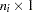 vector for the means of the exogenous variables. There is no model restriction on these subvectors.
vector for the means of the exogenous variables. There is no model restriction on these subvectors.
Summary of Matrices and Submatrices in the RAM Model
Let 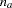 be the total number of manifest and latent variables in the RAM model. Of these
be the total number of manifest and latent variables in the RAM model. Of these 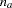 variables,
variables, 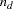 are endogenous and
are endogenous and 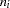 are exogenous. Suppose that the rows and columns of the RAM model matrices
are exogenous. Suppose that the rows and columns of the RAM model matrices  and
and  and the rows of
and the rows of 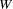 are arranged in the order of
are arranged in the order of 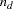 endogenous variables and then
endogenous variables and then 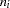 exogenous variables. The names, roles, and dimensions of the RAM model matrices and submatrices are summarized in the following table:
exogenous variables. The names, roles, and dimensions of the RAM model matrices and submatrices are summarized in the following table:
Matrix |
Name |
Description |
Dimensions |
|---|---|---|---|
Model Matrices |
|||
|
_A_ or _RAMA_ |
effects of column variables on row variables, or paths from the column variables to the row variables |
|
|
_P_ or _RAMP_ |
(partial) variances and covariances |
|
|
_W_ or _RAMW_ |
intercepts and means |
|
Submatrices |
|||
|
_RAMBETA_ |
effects of endogenous variables on endogenous variables |
|
|
_RAMGAMMA_ |
effects of exogenous variables on endogenous variables |
|
|
_RAMP11_ |
error variances and covariances for endogenous variables |
|
|
_RAMP21_ |
covariances between exogenous variables and error terms for endogenous variables |
|
|
_RAMP22_ |
variances and covariances for exogenous variables |
|
|
_RAMALPHA_ |
intercepts for endogenous variables |
|
|
_RAMNU_ |
means for exogenous variables |
|
Specification of the RAM Model
In PROC CALIS, the RAM model specification is a matrix-oriented modeling language. That is, you have to define the row and column variables for the model matrices and specify the parameters in terms of matrix entries. This is not the case in PROC TCALIS. You no longer need to specify the RAM model parameters as matrix entries. Instead, you specify the model by using the variable names directly. Representing the RAM model matrices is done internally by PROC TCALIS.
To specify the RAM model parameters, you use the RAM statement to list each parameter location. There are three types of parameter listings, which correspond to the elements in the three model matrices. The three types of parameter listings are described in the following.
(1) Specification of Effects or Paths in Model Matrix 
If in your model there is a path from V2 to V1 and the associated effect parameter is named parm1 with 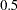 as the starting value, you can use one of the following list-entries of the RAM statement to specify this parameter location:
as the starting value, you can use one of the following list-entries of the RAM statement to specify this parameter location:
_A_ V1 V2 parm1 (0.5),
path V1 <- V2 parm1 (0.5),
path V2 -> V1 parm1 (0.5),
(2) Specification of (Partial) Variances and (Partial) Covariances in Model Matrix 
If V2 is an exogenous variable in the RAM model and you want to specify its variance as a parameter named parm2 with 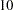 as the starting value, you can use one of the following list-entries of the RAM statement:
as the starting value, you can use one of the following list-entries of the RAM statement:
_P_ V2 V2 parm2 (10.),
pvar V2 parm2 (10.),
If V1 is an endogenous variable in the RAM model and you want to specify its partial variance or error variance as a parameter named parm3 with  as the starting value, you can use one of the following list-entries of the RAM statement:
as the starting value, you can use one of the following list-entries of the RAM statement:
_P_ V1 V1 parm3 (5.),
pvar V1 parm3 (5.),
Notice that this partial variance specification has the same format as that for the variance parameter of an exogenous variable.
If you want to specify (partial) covariance between two variables V3 and V4 as a parameter named parm4 with  as the starting value, you can use one of the following list-entries of the RAM statement:
as the starting value, you can use one of the following list-entries of the RAM statement:
_P_ V3 V4 parm4 (5.),
pcov V3 V4 parm4 (5.),
(3) Specification of Means and Intercepts in Model Matrix _W_
Means and intercepts are specified when the mean structures of the model are of interest. If V5 is an exogenous variable and you want to specify its mean as a parameter named parm5 with  as the starting value, you can use one of the following list-entries of the RAM statement:
as the starting value, you can use one of the following list-entries of the RAM statement:
_W_ V5 parm5 (11.),
mean V5 parm5 (11.),
If V6 is an endogenous variable and you want to specify its intercept as a parameter named parm6 with  as the starting value, you can use one of the following list-entries of the RAM statement:
as the starting value, you can use one of the following list-entries of the RAM statement:
_W_ V6 parm6 (7.),
intercept V6 parm6 (7.),
Note that this specification bears the same format as that for the mean parameter of an exogenous variable.
Specifying Parameters without Initial Values
If you do not have any knowledge about the initial value for a parameter, you can omit the initial value specification and let PROC TCALIS to compute it. For example, you can just provide the parameter locations and parameter names as shown in the following specifications:
_A_ V1 V2 parm1,
intercept V6 parm6,
Specifying Fixed Parameter Values
If you want to specify a fixed parameter value, you do not need to provide the parameter name. Instead, you just provide the fixed value without parentheses at the end of the list-entry. The following shows examples for specifying fixed parameters:
_PCOV_ V3 V4 5.,
mean V5 11.,
A Complete RAM Model Specification Example
Essentially, you can specify all parameters and their locations of the RAM model in the RAM statement. No subsidiary model specification statements are needed in the RAM model—that is, all information regarding the model is specified in the RAM statement. Each parameter location specification is a list-entry in the RAM statement, and these list-entries are separated by commas. For example,
ram
path V1 <- V2 parm1 (.5),
path V1 <- V3 parm2 ,
pvar V1 errv (1.),
pvar V2 parm3 (10.),
pvar V3 parm4 (10.),
pcov V3 V2 parm5 (5.);
Notice that although the order of the list-entries is not critical to the model specification, it is the same order that is used in output displays. See the RAM statement for more details about the syntax.
Default Parameters in the RAM Model
The effect of any variable on itself is restricted to zero in the RAM model. In other words, it is invalid to specify:
ram
path V1 <- V1 parm;
In matrix terms, you cannot have any nonzero diagonal element in the 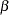 submatrix. All other elements in the RAM model matrices can be specified as free or fixed parameters.
submatrix. All other elements in the RAM model matrices can be specified as free or fixed parameters.
If an element in a model matrix is not subject to model restrictions and is not specified explicitly, a default parameter will be applied to the location. There are two types of default parameters: one is automatic free parameter; and the other is fixed zero.
Automatic Free Parameters
The set of automatic parameters in the RAM model is essentially derived in the same way as those in the LINEQS model. That is, in the LINEQS model the set of automatic parameters includes the variances of and covariances among manifest exogenous variables, the means of manifest exogenous variables when the mean structures are modeled, and the variances of all exogenous latent variables (factors and errors). All these automatic free parameters are applied similarly to the RAM model.
The only difficulty about this generalization is the definition of error variances in the RAM model. Unlike the LINEQS model, error terms in the RAM model are not named explicitly. The question is what the error variances in the LINEQS model correspond to in the RAM model. As described previously, error variances in the RAM model are recast as the partial variances of the corresponding endogenous variables. As a result, the set of automatic parameters in the RAM model includes the variances or partial variances of all variables—that is, variances when the variables are exogenous, partial variances when the variables are endogenous.
As in the LINEQS model, the reason for automatic parameter generation is to safeguard a proper RAM model specification. See the section Rationale of the Default Parameters in the LINEQS Model for a more detailed discussion.
In terms of the RAM model matrices, the set of automatic parameters in the RAM model includes:
all
 matrix diagonal elements, which are either variances of exogenous variables (manifest or latent) or partial variances of endogenous variables (manifest or latent)
matrix diagonal elements, which are either variances of exogenous variables (manifest or latent) or partial variances of endogenous variables (manifest or latent) those
 matrix off-diagonal elements with their rows and columns corresponding to manifest exogenous variables
matrix off-diagonal elements with their rows and columns corresponding to manifest exogenous variables those
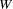 matrix elements with their rows corresponding to manifest exogenous variables, provided that the mean structures are modeled
matrix elements with their rows corresponding to manifest exogenous variables, provided that the mean structures are modeled
Each of these automatic mean, intercept, variance, partial variance, covariance, and partial covariance parameters is named with the prefix _Add, and appended with an unique integer.
Default Fixed Zeros
All unspecified parameter locations that are neither model-restricted nor automatic free parameters in the RAM model matrices are fixed zeros by default.
Relating the RAM Model to the PATH Model
The mathematical model for the RAM and the PATH modeling languages is the same. As a result, the two modeling languages are also quite similar in their syntax. See the section Relating the PATH Model to the RAM Model for details.
Note: This procedure is experimental.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.