Previous Page | Next Page

The ROBUSTREG Procedure

Example 74.3 Growth Study of De Long and Summers

Robust regression and outlier detection techniques have considerable applications to econometrics. The following example from Zaman, Rousseeuw, and Orhan (2001) shows how these techniques substantially improve the ordinary least squares (OLS) results for the growth study of De Long and Summers.

De Long and Summers (1991) studied the national growth of 61 countries from 1960 to 1985 by using OLS with the following data set growth. 

   data growth;
      input country$ GDP LFG EQP NEQ GAP @@;
   datalines;
   Argentin  0.0089 0.0118 0.0214 0.2286 0.6079
   Austria   0.0332 0.0014 0.0991 0.1349 0.5809
   Belgium   0.0256 0.0061 0.0684 0.1653 0.4109
   Bolivia   0.0124 0.0209 0.0167 0.1133 0.8634
   Botswana  0.0676 0.0239 0.1310 0.1490 0.9474
   Brazil    0.0437 0.0306 0.0646 0.1588 0.8498
   Cameroon  0.0458 0.0169 0.0415 0.0885 0.9333
   Canada    0.0169 0.0261 0.0771 0.1529 0.1783
   Chile     0.0021 0.0216 0.0154 0.2846 0.5402
   Colombia  0.0239 0.0266 0.0229 0.1553 0.7695
   CostaRic  0.0121 0.0354 0.0433 0.1067 0.7043
   Denmark   0.0187 0.0115 0.0688 0.1834 0.4079
   Dominica  0.0199 0.0280 0.0321 0.1379 0.8293
   Ecuador   0.0283 0.0274 0.0303 0.2097 0.8205
   ElSalvad  0.0046 0.0316 0.0223 0.0577 0.8414
   Ethiopia  0.0094 0.0206 0.0212 0.0288 0.9805
   Finland   0.0301 0.0083 0.1206 0.2494 0.5589
   France    0.0292 0.0089 0.0879 0.1767 0.4708
   Germany   0.0259 0.0047 0.0890 0.1885 0.4585
   Greece    0.0446 0.0044 0.0655 0.2245 0.7924
   Guatemal  0.0149 0.0242 0.0384 0.0516 0.7885
   Honduras  0.0148 0.0303 0.0446 0.0954 0.8850
   HongKong  0.0484 0.0359 0.0767 0.1233 0.7471
   India     0.0115 0.0170 0.0278 0.1448 0.9356
   Indonesi  0.0345 0.0213 0.0221 0.1179 0.9243
   Ireland   0.0288 0.0081 0.0814 0.1879 0.6457
   Israel    0.0452 0.0305 0.1112 0.1788 0.6816
   Italy     0.0362 0.0038 0.0683 0.1790 0.5441
   IvoryCoa  0.0278 0.0274 0.0243 0.0957 0.9207
   Jamaica   0.0055 0.0201 0.0609 0.1455 0.8229
   Japan     0.0535 0.0117 0.1223 0.2464 0.7484
   Kenya     0.0146 0.0346 0.0462 0.1268 0.9415
   Korea     0.0479 0.0282 0.0557 0.1842 0.8807
   Luxembou  0.0236 0.0064 0.0711 0.1944 0.2863
   Madagasc -0.0102 0.0203 0.0219 0.0481 0.9217
   Malawi    0.0153 0.0226 0.0361 0.0935 0.9628
   Malaysia  0.0332 0.0316 0.0446 0.1878 0.7853
   Mali      0.0044 0.0184 0.0433 0.0267 0.9478
   Mexico    0.0198 0.0349 0.0273 0.1687 0.5921
   Morocco   0.0243 0.0281 0.0260 0.0540 0.8405
   Netherla  0.0231 0.0146 0.0778 0.1781 0.3605
   Nigeria  -0.0047 0.0283 0.0358 0.0842 0.8579
   Norway    0.0260 0.0150 0.0701 0.2199 0.3755
   Pakistan  0.0295 0.0258 0.0263 0.0880 0.9180
   Panama    0.0295 0.0279 0.0388 0.2212 0.8015
   Paraguay  0.0261 0.0299 0.0189 0.1011 0.8458
   Peru      0.0107 0.0271 0.0267 0.0933 0.7406
   Philippi  0.0179 0.0253 0.0445 0.0974 0.8747
   Portugal  0.0318 0.0118 0.0729 0.1571 0.8033
   Senegal  -0.0011 0.0274 0.0193 0.0807 0.8884
   Spain     0.0373 0.0069 0.0397 0.1305 0.6613
   SriLanka  0.0137 0.0207 0.0138 0.1352 0.8555
   Tanzania  0.0184 0.0276 0.0860 0.0940 0.9762
   Thailand  0.0341 0.0278 0.0395 0.1412 0.9174
   Tunisia   0.0279 0.0256 0.0428 0.0972 0.7838
   U.K.      0.0189 0.0048 0.0694 0.1132 0.4307
   U.S.      0.0133 0.0189 0.0762 0.1356 0.0000
   Uruguay   0.0041 0.0052 0.0155 0.1154 0.5782
   Venezuel  0.0120 0.0378 0.0340 0.0760 0.4974
   Zambia   -0.0110 0.0275 0.0702 0.2012 0.8695
   Zimbabwe  0.0110 0.0309 0.0843 0.1257 0.8875
   ;

The regression equation they used is

     

where the response variable is the growth in gross domestic product per worker (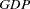) and the regressors are labor force growth (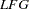), relative GDP gap (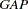), equipment investment (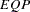), and nonequipment investment ().

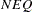The following statements invoke the REG procedure ( Chapter 73, The REG Procedure ) for the OLS analysis: 

   proc reg data=growth;
      model GDP  = LFG GAP EQP NEQ ;
   run;

Output 74.3.1 OLS Estimates
The REG Procedure
Model: MODEL1
Dependent Variable: GDP

Parameter Estimates
Variable DF Parameter
Estimate		 Standard
Error		 t Value Pr > |t|
Intercept 1 -0.01430 0.01028 -1.39 0.1697
LFG 1 -0.02981 0.19838 -0.15 0.8811
GAP 1 0.02026 0.00917 2.21 0.0313
EQP 1 0.26538 0.06529 4.06 0.0002
NEQ 1 0.06236 0.03482 1.79 0.0787

The OLS analysis shown in Output 74.3.1 indicates that 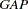and 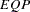have a significant influence on 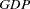at the 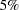level.

The following statements invoke the ROBUSTREG procedure with the default M estimation. 

   ods graphics on;
    
   proc robustreg data=growth plots=all;
      model GDP  = LFG GAP EQP NEQ / diagnostics leverage;
      id country;
   run;
    
   ods graphics off;

Output 74.3.2 displays model information and summary statistics for variables in the model.

Output 74.3.2 Model Fitting Information and Summary Statistics
The ROBUSTREG Procedure

Model Information
Data Set WORK.GROWTH
Dependent Variable GDP
Number of Independent Variables 4
Number of Observations 61
Method M Estimation

Summary Statistics
Variable Q1 Median Q3 Mean Standard
Deviation		 MAD
LFG 0.0118 0.0239 0.0281 0.0211 0.00979 0.00949
GAP 0.5796 0.8015 0.8863 0.7258 0.2181 0.1778
EQP 0.0265 0.0433 0.0720 0.0523 0.0296 0.0325
NEQ 0.0956 0.1356 0.1812 0.1399 0.0570 0.0624
GDP 0.0121 0.0231 0.0310 0.0224 0.0155 0.0150

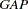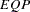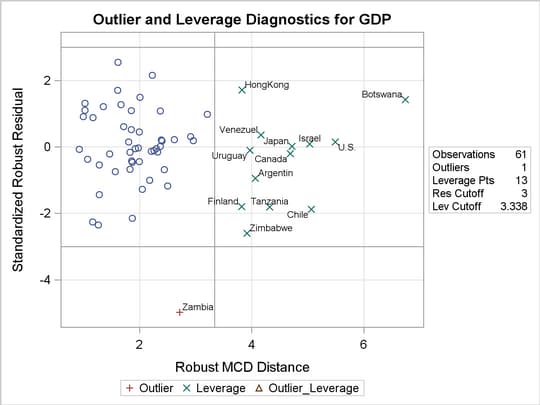
Output 74.3.3 displays the M estimates. Besides and , the robust analysis also indicates that 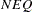is significant. This new finding is explained by Output 74.3.4, which shows that Zambia, the 60th country in the data, is an outlier. Output 74.3.4 also identifies leverage points based on the robust MCD distances; however, there are no serious high-leverage points in this data set.

Output 74.3.3 M Estimates
Parameter Estimates
Parameter DF Estimate Standard Error 95% Confidence Limits Chi-Square Pr > ChiSq
Intercept 1 -0.0247 0.0097 -0.0437 -0.0058 6.53 0.0106
LFG 1 0.1040 0.1867 -0.2619 0.4699 0.31 0.5775
GAP 1 0.0250 0.0086 0.0080 0.0419 8.36 0.0038
EQP 1 0.2968 0.0614 0.1764 0.4172 23.33 <.0001
NEQ 1 0.0885 0.0328 0.0242 0.1527 7.29 0.0069
Scale 1 0.0099          

Output 74.3.4 Diagnostics
Diagnostics
Obs country Mahalanobis Distance Robust MCD Distance Leverage Standardized
Robust Residual		 Outlier
1 Argentin 2.6083 4.0639 * -0.9424  
5 Botswana 3.4351 6.7391 * 1.4200  
8 Canada 3.1876 4.6843 * -0.1972  
9 Chile 3.6752 5.0599 * -1.8784  
17 Finland 2.6024 3.8186 * -1.7971  
23 HongKong 2.1225 3.8238 * 1.7161  
27 Israel 2.6461 5.0336 * 0.0909  
31 Japan 2.9179 4.7140 * 0.0216  
53 Tanzania 2.2600 4.3193 * -1.8082  
57 U.S. 3.8701 5.4874 * 0.1448  
58 Uruguay 2.5953 3.9671 * -0.0978  
59 Venezuel 2.9239 4.1663 * 0.3573  
60 Zambia 1.8562 2.7135   -4.9798 *
61 Zimbabwe 1.9634 3.9128 * -2.5959  

Figure 74.3.5 displays robust versions of goodness-of-fit statistics for the model.

Output 74.3.5 Goodness-of-Fit Statistics
Goodness-of-Fit
Statistic Value
R-Square 0.3178
AICR 80.2134
BICR 91.5095
Deviance 0.0070

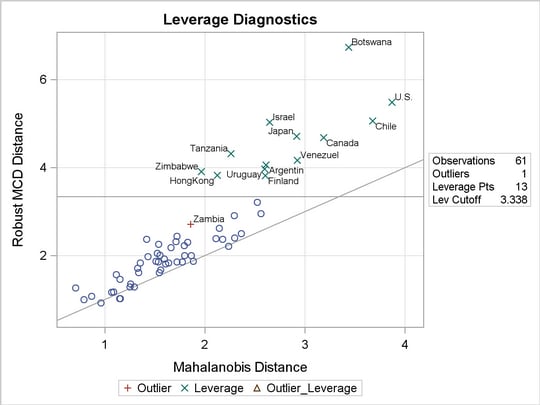
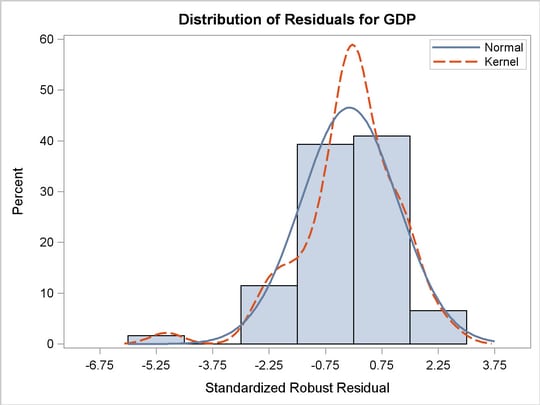
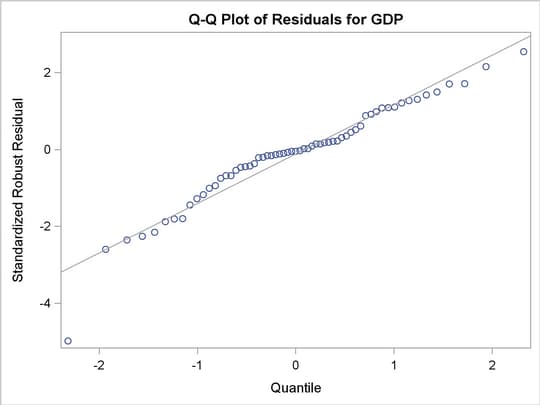
The PLOTS=ALL option generates four diagnostic plots. Figure 74.3.6 and Figure 74.3.7 are for outlier and leverage-point diagnostics. Figure 74.3.8 and Figure 74.3.9 are a histogram and a Q-Q plot of the standardized robust residuals, respectively.

Output 74.3.6 RDPLOT for Stackloss Data
RDPLOT for Stackloss Data

Output 74.3.7 DDPLOT for Stackloss Data
DDPLOT for Stackloss Data

Output 74.3.8 Histogram
Histogram

Output 74.3.9 Q-Q Plot
Q-Q Plot

The following statements invoke the ROBUSTREG procedure with LTS estimation, which was used by Zaman, Rousseeuw, and Orhan (2001). The results are consistent with those of M estimation. 

   proc robustreg method=lts(h=33) fwls data=growth;
      model GDP  = LFG GAP EQP NEQ / diagnostics leverage ;
      id country;
   run;

Output 74.3.10 LTS Estimates
The ROBUSTREG Procedure

LTS Parameter Estimates
Parameter DF Estimate
Intercept 1 -0.0249
LFG 1 0.1123
GAP 1 0.0214
EQP 1 0.2669
NEQ 1 0.1110
Scale (sLTS) 0 0.0076
Scale (Wscale) 0 0.0109

Output 74.3.10 displays the LTS estimates.

Output 74.3.11 Diagnostics and LTS R Square
Diagnostics
Obs country Mahalanobis Distance Robust MCD Distance Leverage Standardized
Robust Residual		 Outlier
1 Argentin 2.6083 4.0639 * -1.0715  
5 Botswana 3.4351 6.7391 * 1.6574  
8 Canada 3.1876 4.6843 * -0.2324  
9 Chile 3.6752 5.0599 * -2.0896  
17 Finland 2.6024 3.8186 * -1.6367  
23 HongKong 2.1225 3.8238 * 1.7570  
27 Israel 2.6461 5.0336 * 0.2334  
31 Japan 2.9179 4.7140 * 0.0971  
53 Tanzania 2.2600 4.3193 * -1.2978  
57 U.S. 3.8701 5.4874 * 0.0605  
58 Uruguay 2.5953 3.9671 * -0.0857  
59 Venezuel 2.9239 4.1663 * 0.4113  
60 Zambia 1.8562 2.7135   -4.4984 *
61 Zimbabwe 1.9634 3.9128 * -2.1201  

R-Square for LTS Estimation
R-Square 0.7418

Output 74.3.11 displays outlier and leverage-point diagnostics based on the LTS estimates.

Output 74.3.12 Final Weighted LS Estimates
Parameter Estimates for Final Weighted Least Squares Fit
Parameter DF Estimate Standard Error 95% Confidence Limits Chi-Square Pr > ChiSq
Intercept 1 -0.0222 0.0093 -0.0405 -0.0039 5.65 0.0175
LFG 1 0.0446 0.1771 -0.3026 0.3917 0.06 0.8013
GAP 1 0.0245 0.0082 0.0084 0.0406 8.89 0.0029
EQP 1 0.2824 0.0581 0.1685 0.3964 23.60 <.0001
NEQ 1 0.0849 0.0314 0.0233 0.1465 7.30 0.0069
Scale 0 0.0116          

Output 74.3.12 displays the final weighted least squares estimates, which are identical to those reported in Zaman, Rousseeuw, and Orhan (2001).

Previous Page | Next Page | Top of Page

Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.