| The CANDISC Procedure |
Getting Started: CANDISC Procedure
The data in this example are measurements of 159 fish caught in Finland’s lake Laengelmavesi; this data set is available from the Puranen. For each of the For each of the seven species (bream, roach, whitefish, parkki, perch, pike, and smelt) the weight, length, height, and width of each fish are tallied. Three different length measurements are recorded: from the nose of the fish to the beginning of its tail, from the nose to the notch of its tail, and from the nose to the end of its tail. The height and width are recorded as percentages of the third length variable. The following statements create the SAS data set:
title 'Fish Measurement Data';
proc format;
value specfmt
1='Bream'
2='Roach'
3='Whitefish'
4='Parkki'
5='Perch'
6='Pike'
7='Smelt';
run;
data fish (drop=HtPct WidthPct);
input Species Weight Length1 Length2 Length3 HtPct
WidthPct @@;
Height=HtPct*Length3/100;
Width=WidthPct*Length3/100;
format Species specfmt.;
symbol = put(Species, specfmt2.);
datalines;
1 242.0 23.2 25.4 30.0 38.4 13.4 1 290.0 24.0 26.3 31.2 40.0 13.8
... more lines ...
7 19.7 13.2 14.3 15.2 18.9 13.6 7 19.9 13.8 15.0 16.2 18.1 11.6
;
The next steps use PROC CANDISC to find the three canonical variables that best separate the species of fish in the fish data and create the output data set outcan. With the NCAN=3 option, only the first three canonical variables are displayed. The ODS EXCLUDE statement is specified to exclude the canonical structure tables and most of the canonical coefficient tables in order to obtain a more compact set of results. The TEMPLATE and SGRENDER procedures within ODS Graphics are invoked to create a plot of the first two canonical variables. The following statements produce Figure 27.1 through Figure 27.6:
proc candisc data=fish ncan=3 out=outcan;
ods exclude tstruc bstruc pstruc tcoef pcoef;
class Species;
var Weight Length1 Length2 Length3 Height Width;
run;
proc template;
define statgraph scatter;
begingraph;
entrytitle 'Fish Measurement Data';
layout overlayequated / equatetype=fit
xaxisopts=(label='Canonical Variable 1')
yaxisopts=(label='Canonical Variable 2');
scatterplot x=Can1 y=Can2 / group=species name='fish';
layout gridded / autoalign=(topright);
discretelegend 'fish' / border=false opaque=false;
endlayout;
endlayout;
endgraph;
end;
run;
proc sgrender data=outcan template=scatter;
run;
PROC CANDISC begins by displaying summary information about the variables in the analysis. This information includes the number of observations, the number of quantitative variables in the analysis (specified with the VAR statement), and the number of classes in the classification variable (specified with the CLASS statement). The frequency of each class is also displayed.
| Total Sample Size | 158 | DF Total | 157 |
|---|---|---|---|
| Variables | 6 | DF Within Classes | 151 |
| Classes | 7 | DF Between Classes | 6 |
| Class Level Information | ||||
|---|---|---|---|---|
| Species | Variable Name |
Frequency | Weight | Proportion |
| Bream | Bream | 34 | 34.0000 | 0.215190 |
| Parkki | Parkki | 11 | 11.0000 | 0.069620 |
| Perch | Perch | 56 | 56.0000 | 0.354430 |
| Pike | Pike | 17 | 17.0000 | 0.107595 |
| Roach | Roach | 20 | 20.0000 | 0.126582 |
| Smelt | Smelt | 14 | 14.0000 | 0.088608 |
| Whitefish | Whitefish | 6 | 6.0000 | 0.037975 |
PROC CANDISC performs a multivariate one-way analysis of variance (one-way MANOVA) and provides four multivariate tests of the hypothesis that the class mean vectors are equal. These tests, shown in Figure 27.2, indicate that not all of the mean vectors are equal 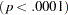 .
.
| Multivariate Statistics and F Approximations | |||||
|---|---|---|---|---|---|
| S=6 M=-0.5 N=72 | |||||
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.00036325 | 90.71 | 36 | 643.89 | <.0001 |
| Pillai's Trace | 3.10465132 | 26.99 | 36 | 906 | <.0001 |
| Hotelling-Lawley Trace | 52.05799676 | 209.24 | 36 | 413.64 | <.0001 |
| Roy's Greatest Root | 39.13499776 | 984.90 | 6 | 151 | <.0001 |
| NOTE: F Statistic for Roy's Greatest Root is an upper bound. | |||||
The first canonical correlation is the greatest possible multiple correlation with the classes that can be achieved by using a linear combination of the quantitative variables. The first canonical correlation, displayed in Figure 27.3, is 0.987463. A likelihood ratio test is displayed of the hypothesis that the current canonical correlation and all smaller ones are zero. The first line is equivalent to Wilks’ lambda multivariate test.
| Canonical Correlation |
Adjusted Canonical Correlation |
Approximate Standard Error |
Squared Canonical Correlation |
Eigenvalues of Inv(E)*H = CanRsq/(1-CanRsq) |
Test of H0: The canonical correlations in the current row and all that follow are zero | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | Likelihood Ratio |
Approximate F Value |
Num DF | Den DF | Pr > F | |||||
| 1 | 0.987463 | 0.986671 | 0.001989 | 0.975084 | 39.1350 | 29.3859 | 0.7518 | 0.7518 | 0.00036325 | 90.71 | 36 | 643.89 | <.0001 |
| 2 | 0.952349 | 0.950095 | 0.007425 | 0.906969 | 9.7491 | 7.3786 | 0.1873 | 0.9390 | 0.01457896 | 46.46 | 25 | 547.58 | <.0001 |
| 3 | 0.838637 | 0.832518 | 0.023678 | 0.703313 | 2.3706 | 1.7016 | 0.0455 | 0.9846 | 0.15671134 | 23.61 | 16 | 452.79 | <.0001 |
| 4 | 0.633094 | 0.623649 | 0.047821 | 0.400809 | 0.6689 | 0.5346 | 0.0128 | 0.9974 | 0.52820347 | 12.09 | 9 | 362.78 | <.0001 |
| 5 | 0.344157 | 0.334170 | 0.070356 | 0.118444 | 0.1344 | 0.1343 | 0.0026 | 1.0000 | 0.88152702 | 4.88 | 4 | 300 | 0.0008 |
| 6 | 0.005701 | . | 0.079806 | 0.000033 | 0.0000 | 0.0000 | 1.0000 | 0.99996749 | 0.00 | 1 | 151 | 0.9442 | |
The first canonical variable, Can1, shows that the linear combination of the centered variables Can1 0.0006
0.0006 Weight – 0.33
Weight – 0.33 Length1 – 2.49
Length1 – 2.49 Length2
Length2 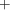 2.60
2.60 Length3
Length3 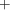 1.12
1.12 Height – 1.45
Height – 1.45 Width separates the species most effectively (see Figure 27.4).
Width separates the species most effectively (see Figure 27.4).
| Raw Canonical Coefficients | |||
|---|---|---|---|
| Variable | Can1 | Can2 | Can3 |
| Weight | -0.000648508 | -0.005231659 | -0.005596192 |
| Length1 | -0.329435762 | -0.626598051 | -2.934324102 |
| Length2 | -2.486133674 | -0.690253987 | 4.045038893 |
| Length3 | 2.595648437 | 1.803175454 | -1.139264914 |
| Height | 1.121983854 | -0.714749340 | 0.283202557 |
| Width | -1.446386704 | -0.907025481 | 0.741486686 |
PROC CANDISC computes the means of the canonical variables for each class. The first canonical variable is the linear combination of the variables Weight, Length1, Length2, Length3, Height, and Width that provides the greatest difference (in terms of a univariate  test) between the class means. The second canonical variable provides the greatest difference between class means while being uncorrelated with the first canonical variable.
test) between the class means. The second canonical variable provides the greatest difference between class means while being uncorrelated with the first canonical variable.
| Class Means on Canonical Variables | |||
|---|---|---|---|
| Species | Can1 | Can2 | Can3 |
| Bream | 10.94142464 | 0.52078394 | 0.23496708 |
| Parkki | 2.58903743 | -2.54722416 | -0.49326158 |
| Perch | -4.47181389 | -1.70822715 | 1.29281314 |
| Pike | -4.89689441 | 8.22140791 | -0.16469132 |
| Roach | -0.35837149 | 0.08733611 | -1.10056438 |
| Smelt | -4.09136653 | -2.35805841 | -4.03836098 |
| Whitefish | -0.39541755 | -0.42071778 | 1.06459242 |
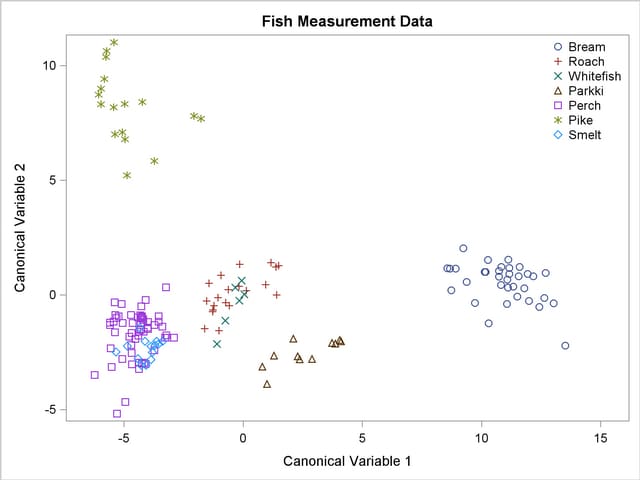
A plot of the first two canonical variables (Figure 27.6) shows that Can1 discriminates between three groups: 1) bream; 2) whitefish, roach, and parkki; and 3) smelt, pike, and perch. Can2 best discriminates between pike and the other species.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.