The HPQUANTSELECT Procedure
Quasi-likelihood Information Criteria
Given the quantile level  , assume that the distribution of
, assume that the distribution of 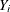 conditional on
conditional on 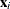 follows the linear model
follows the linear model
![\[ Y_ i = \mb{x}_ i^{\prime }\bbeta + \epsilon _ i \]](images/stathpug_hpqtr0030.png)
where 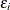 for
for 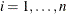 are iid in distribution F. Further assume that F is an asymmetric Laplace distribution whose density function is
are iid in distribution F. Further assume that F is an asymmetric Laplace distribution whose density function is
![\[ f_\tau (r)={\tau (1-\tau )\over \sigma }\exp \left(-{\rho _\tau (r)\over \sigma }\right) \]](images/stathpug_hpqtr0095.png)
where  is the scale parameter. Then, the negative log-likelihood function is
is the scale parameter. Then, the negative log-likelihood function is
![\[ l_\tau (\bbeta ,\sigma )=n\log (\sigma )+\sigma ^{-1}\sum _{i=1}^ n\rho _\tau (y_ i-\mb{x}_ i’\bbeta )-n\log (\tau (1-\tau )) \]](images/stathpug_hpqtr0097.png)
Under these settings, the maximum likelihood estimate (MLE) of 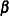 is the same as the relevant level-
is the same as the relevant level- quantile regression solution
quantile regression solution 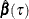 , and the MLE for
, and the MLE for  is
is
![\[ \hat{\sigma }(\tau )=n^{-1}\sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\hat{\bbeta }(\tau )\right) \]](images/stathpug_hpqtr0100.png)
where 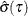 equals the level-
equals the level- average check loss
average check loss 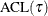 for the quantile regression solution.
for the quantile regression solution.
Because the general form of Akaike’s information criterion (AIC) is 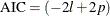 , the quasi-likelihood AIC for quantile regression is
, the quasi-likelihood AIC for quantile regression is
![\[ \mbox{AIC}(\tau )=2n\ln \left( \mbox{ACL}(\tau ) \right) + 2p \]](images/stathpug_hpqtr0104.png)
where p is the degrees of freedom for the fitted model.
Similarly, the quasi-likelihood AICC (corrected AIC) and SBC (Schwarz Bayesian information criterion) can be formulated as follows:
![\[ \mbox{AICC}(\tau )=2n\ln \left(\mbox{ACL}(\tau )\right)+{2pn\over n-p-1} \]](images/stathpug_hpqtr0105.png)
![\[ \mbox{SBC}(\tau )=2n\ln \left(\mbox{ACL}(\tau )\right)+p\ln (n) \]](images/stathpug_hpqtr0106.png)
In fact, the quasi-likelihood AIC, AICC, and SBC are fairly robust, and you can use them to select effects for data sets without the iid assumption in asymmetric Laplace distribution. For a simulation study that applies SBC for effect selection, see Simulation Study. The study generates a data set by using a naive instrumental model (Chernozhukov and Hansen 2008).
