The HPQUANTSELECT Procedure
Linear Model with iid Errors
You can specify the SPARSITY(IID) option in the MODEL
statement to assume that the distribution of 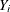 conditional on
conditional on 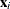 follows the linear model
follows the linear model
![\[ Y_ i = \mb{x}_ i^{\prime }\bbeta + \epsilon _ i \]](images/stathpug_hpqtr0030.png)
where 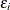 for
for 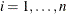 are iid in the distribution function F. Let
are iid in the distribution function F. Let 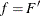 denote the density function of F. Further assume that
denote the density function of F. Further assume that 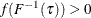 in a neighborhood of
in a neighborhood of  . Then, under some mild conditions, Koenker and Bassett (1982) prove that the asymptotic distribution of the quantile regression estimates is
. Then, under some mild conditions, Koenker and Bassett (1982) prove that the asymptotic distribution of the quantile regression estimates is
![\[ \sqrt {n}({\hat\bbeta }(\tau ) - \bbeta (\tau )) \rightarrow N(0, \omega ^2(\tau , F) \bOmega ^{-1}) \]](images/stathpug_hpqtr0034.png)
where 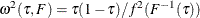 and
and 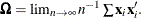 The reciprocal of the density function,
The reciprocal of the density function, 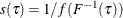 , is called the sparsity function.
, is called the sparsity function.
Accordingly, the covariance matrix of 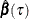 can be estimated as
can be estimated as
![\[ \hat{\Sigma }(\tau )=\tau (1-\tau )\hat{s}^2(\tau )(\mb{X}’\mb{X})^{-} \]](images/stathpug_hpqtr0039.png)
where 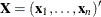 is the design matrix and
is the design matrix and 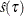 is an estimate of
is an estimate of 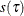 . Under the iid assumption, the algorithm for computing
. Under the iid assumption, the algorithm for computing 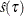 is as follows:
is as follows:
-
Fit a quantile regression model and compute the residuals. Each residual
 can be viewed as an estimated realization of the corresponding error
can be viewed as an estimated realization of the corresponding error 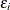 .
.
-
Compute the quantile level bandwidth
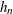 . The HPQUANTSELECT procedure provides two bandwidth methods:
. The HPQUANTSELECT procedure provides two bandwidth methods:
-
The Bofinger bandwidth is an optimizer of mean squared error for standard density estimation:
![\[ h_ n = n^{-1\slash 5} ( {4.5v^2(\tau )} )^{1\slash 5} \]](images/stathpug_hpqtr0045.png)
-
The Hall-Sheather bandwidth is based on Edgeworth expansions for studentized quantiles,
![\[ h_ n = n^{-1\slash 3} z_\alpha ^{2\slash 3} ( {1.5 v(\tau )} )^{1\slash 3} \]](images/stathpug_hpqtr0046.png)
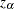 satisfies
satisfies 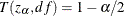 for the construction of
for the construction of 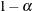 confidence intervals, where T is the cumulative distribution function for the t distribution and
confidence intervals, where T is the cumulative distribution function for the t distribution and 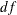 is the residual degrees of freedom.
is the residual degrees of freedom.
The quantity
![\[ v(\tau ) = {\frac{s(\tau )}{s^{(2)}(\tau )}} = {\frac{f^2}{2(f^{(1)} \slash f)^2 + [(f^{(1)} \slash f)^2 - f^{(2)}\slash f ] }} \]](images/stathpug_hpqtr0051.png)
is not sensitive to f and can be estimated by assuming f is Gaussian as
![\[ \hat{v}(\tau )={{\exp (-q^2)} \over 2\pi (q^2+1)} \]](images/stathpug_hpqtr0052.png)
where
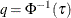 .
.
-
-
Compute residual quantiles
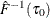 and
and 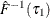 as follows:
as follows:
-
Set
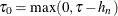 and
and 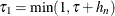 .
.
-
Use the equation
![\[ {\hat F}^{-1}(t) = \left\{ \begin{array}{ll} r_{(1)} & {\mbox{if }} t\in [0, 1\slash 2n) \\ \lambda r_{(i+1)} + (1-\lambda ) r_{(i)} & {\mbox{if }} t\in [(i-0.5)\slash n, (i+0.5)\slash n) \\ r_{(n)} & {\mbox{if }} t\in [(2n-1), 1] \\ \end{array} \right. \]](images/stathpug_hpqtr0058.png)
where
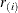 is the ith smallest residual and
is the ith smallest residual and 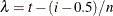 .
.
-
If
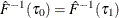 , find i that satisfies
, find i that satisfies 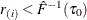 and
and 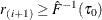 . If such an i exists, reset
. If such an i exists, reset 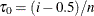 so that
so that 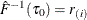 . Also find j that satisfies
. Also find j that satisfies 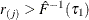 and
and 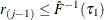 . If such a j exists, reset
. If such a j exists, reset 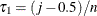 so that
so that 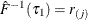 .
.
-
-
Estimate the sparsity function
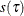 as
as
![\[ \hat{s}(\tau )={{\hat{F}^{-1}(\tau _1)-\hat{F}^{-1}(\tau _0)} \over {\tau _1-\tau _0}} \]](images/stathpug_hpqtr0070.png)
